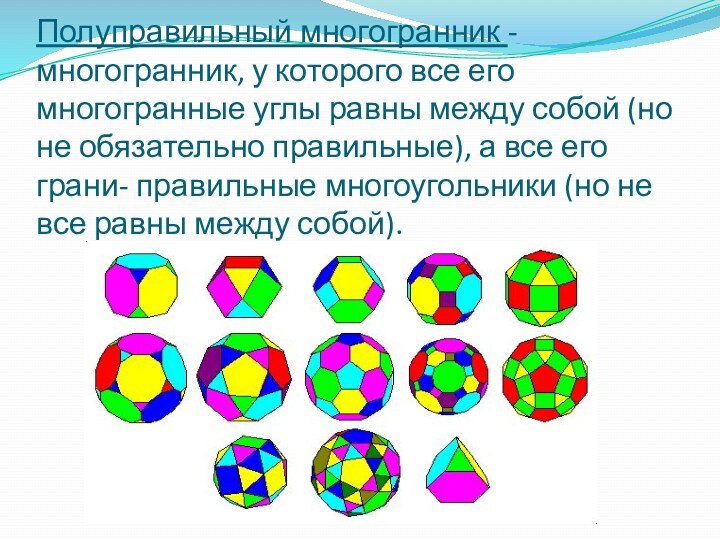
углы равны между собой (но не обязательно правильные), а
все его грани- правильные многоугольники (но не все равны между собой).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


























Национальная библиотека Беларуси.