- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многогранники
Содержание
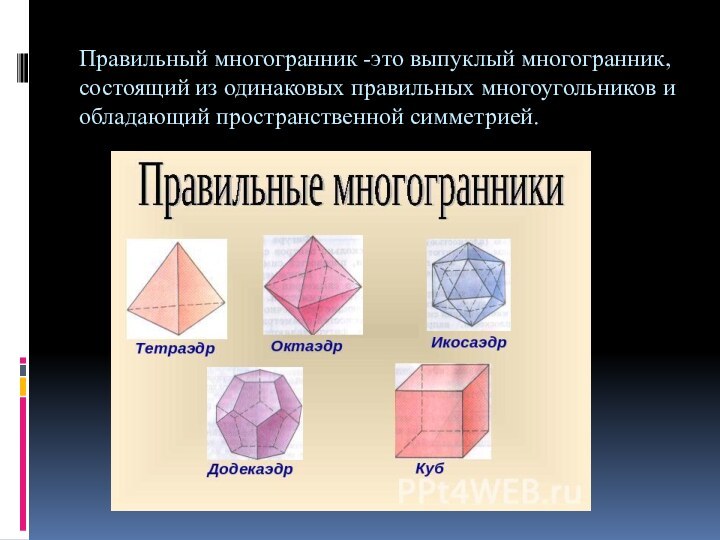
- 2. Правильный многогранник -это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.
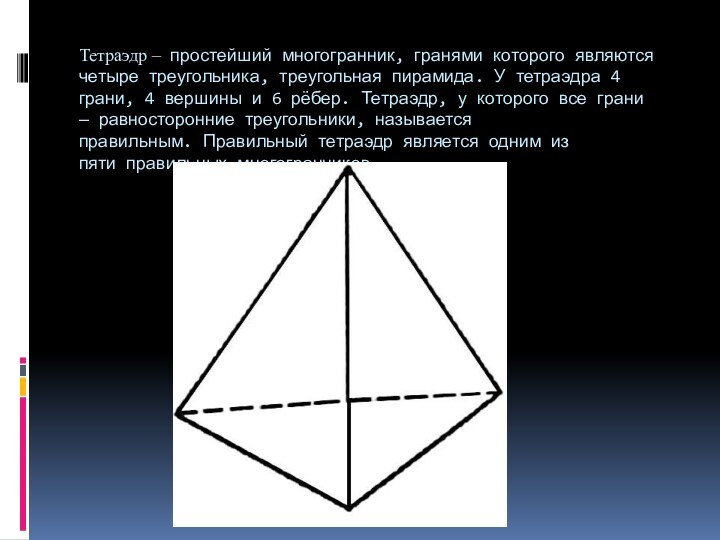
- 3. Тетраэдр – простейший многогранник, гранями которого являются
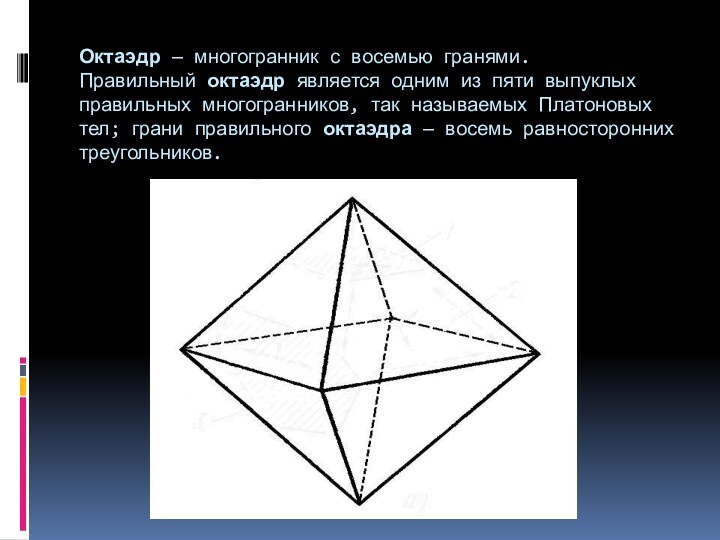
- 4. Октаэдр — многогранник с восемью гранями. Правильный октаэдр является одним
- 5. Икосаэдр — правильный выпуклый многогранник, двадцатигранник, одно
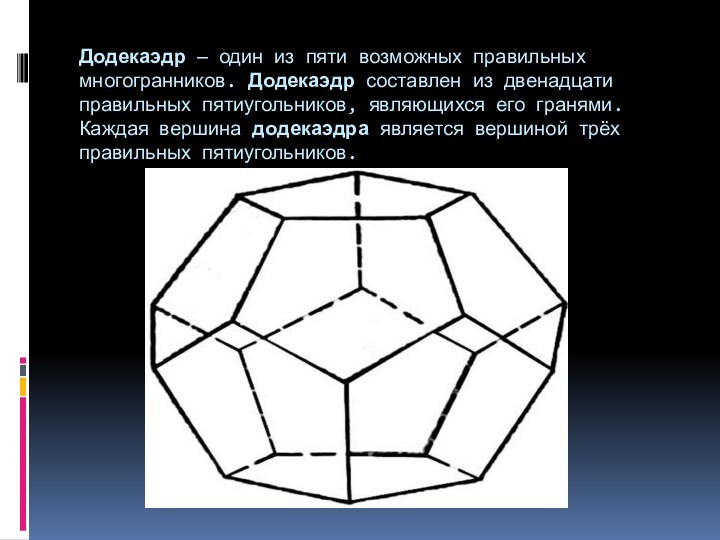
- 6. Додекаэдр — один из пяти возможных правильных многогранников. Додекаэдр составлен
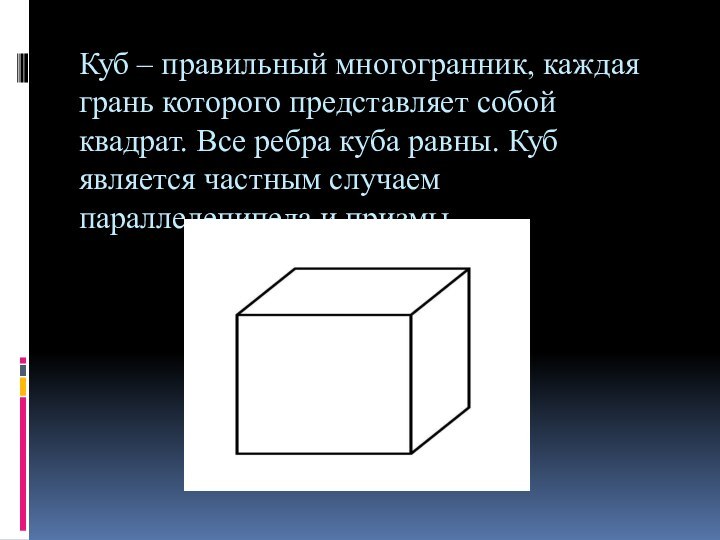
- 7. Куб – правильный многогранник, каждая грань которого
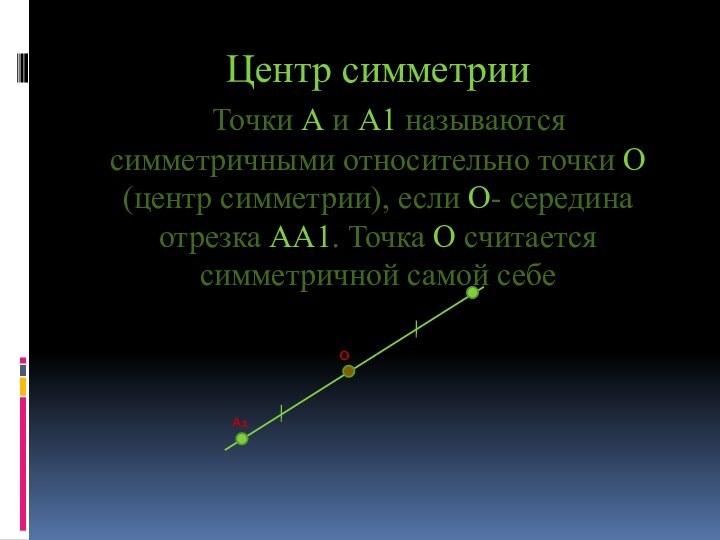
- 8. Центр симметрии Точки А и А1
- 9. Ось симметрии Точки А и А1
- 10. Скачать презентацию
- 11. Похожие презентации
Правильный многогранник -это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.