Презентация на тему Правильные многогранники. Симметрия в пространстве

Содержание

3. {Этимология}Симме́три́я слово произошло от:др.греч.συμμετρία «соразмерность»μετρέω — «меряю»в широком смысле — соответствие, неизменность.
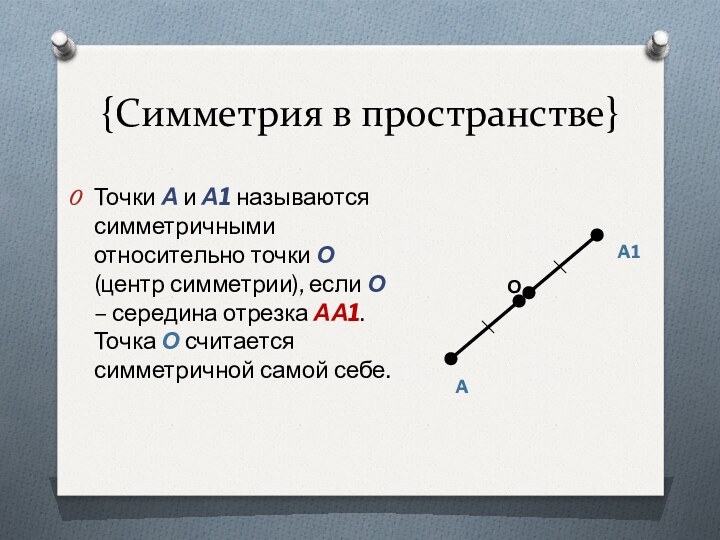
4. {Симметрия в пространстве}Точки А и А1 называются
5. {Осевая симметрия}Точки А и А1 называются симметричными
6. {Плоскость симметрии}Точки А и А1 называются симметричными
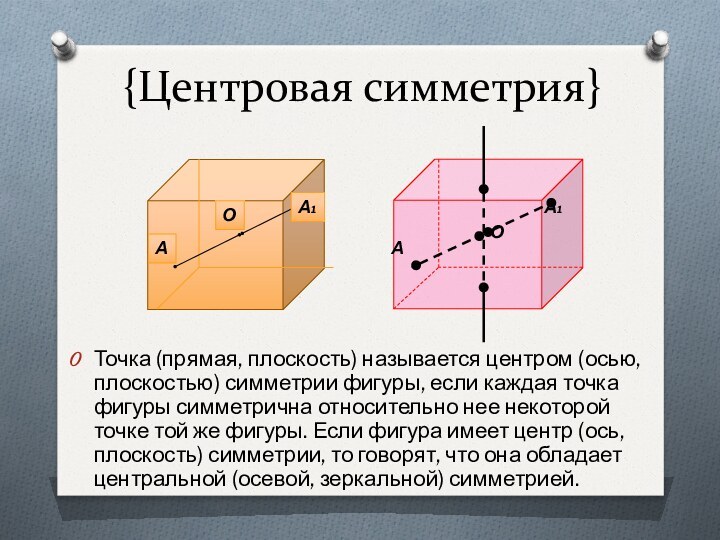
7. {Центровая симметрия}Точка (прямая, плоскость) называется центром (осью,
8. {Правильные многогранники} Платоновые телаимеют в качестве граней
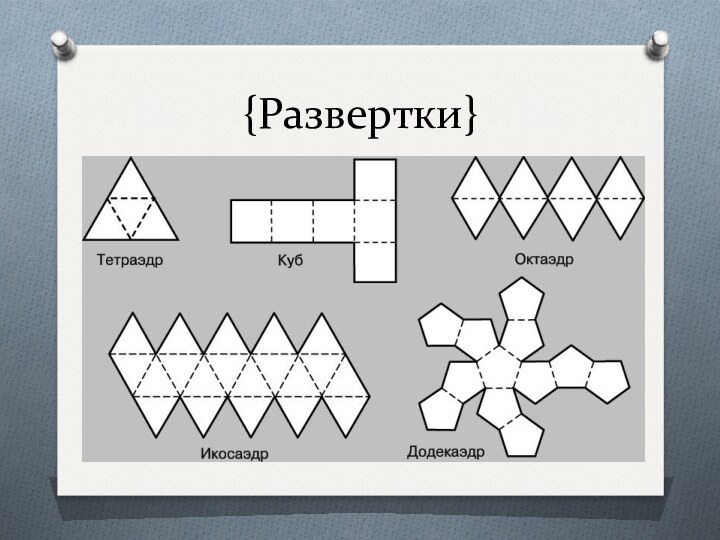
9. {Развертки}
10. {Симметрия в природе}Снежинки
11. {МГУ} самый знаменитый пример в архитектуре
12. Скачать презентацию
13. Похожие презентации

{Этимология}Симме́три́я слово произошло от:др.греч.συμμετρία «соразмерность»μετρέω — «меряю»в широком смысле — соответствие, неизменность.

Главная
Математика
Правильные многогранники. Симметрия в пространстве

Презентация по геометрии на тему: «Правильные многогранники. Симметрия в пространстве»Выполнила ученица

Правильные многогранники. Симметрия в пространстве

{Этимология}Симме́три́я слово произошло от:др.греч.συμμετρία «соразмерность»μετρέω — «меряю»в широком смысле — соответствие, неизменность.

{Симметрия в пространстве}Точки А и А1 называются симметричными относительно точки О (центр

{Осевая симметрия}Точки А и А1 называются симметричными относительно прямой (ось симметрии), если

{Плоскость симметрии}Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если

{Центровая симметрия}Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая

{Правильные многогранники} Платоновые телаимеют в качестве граней конгруэнтные правильные многоугольники, причем число

{МГУ} самый знаменитый пример в архитектуре

Слайды презентации

Слайд 2

Слайд 3 {Этимология}
Симме́три́я слово произошло от:
др.греч.
συμμετρία
«соразмерность»
μετρέω — «меряю»

в широком смысле — соответствие,

неизменность.

Слайд 4 {Симметрия в пространстве}
Точки А и А1 называются симметричными

{Симметрия в пространстве}Точки А и А1 называются симметричными относительно точки О

относительно точки О (центр симметрии), если О – середина

отрезка АА1. Точка О считается симметричной самой себе.

Слайд 5 {Осевая симметрия}
Точки А и А1 называются симметричными относительно

{Осевая симметрия}Точки А и А1 называются симметричными относительно прямой (ось симметрии),

прямой (ось симметрии), если прямая проходит через середину отрезка

АА1 и перпендикулярна этому отрезку. Каждая точка прямой а считается симметричной самой себе. Лист, снежинка, бабочка – примеры осевой симметрии.

Слайд 6 {Плоскость симметрии}
Точки А и А1 называются симметричными относительно

{Плоскость симметрии}Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии),

плоскости (плоскость симметрии), если эта плоскость проходит через середину

отрезка АА1 и перпендикулярна этому отрезку. Каждая точка плоскости считается симметричной самой себе.

Слайд 7 {Центровая симметрия}
Точка (прямая, плоскость) называется центром (осью, плоскостью)

{Центровая симметрия}Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если

симметрии фигуры, если каждая точка фигуры симметрична относительно нее

некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.