последовательностей
Возрастание и убывание числовых последовательностей
Предел числовой последовательности
Гармонический ряд
Свойства
пределовПримеры
Сумма бесконечной геометрической прогрессии
Предел функции на бесконечности
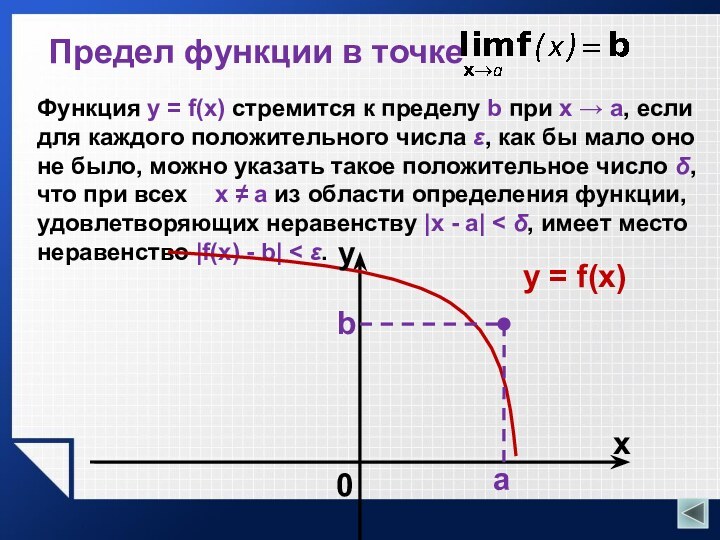
Предел функции в точке
Непрерывность функции в точке