стремящемся к бесконечности,
если для любого, сколь угодно малого
числа ε>0, найдется такое положительное число
S, что при всех |x|>S, выполняется
неравенство:
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Предел функции в бесконечности и в точке
Содержание
- 2. Число А называется пределом функции у=f(x), при
- 3. При достаточно больших по модулю значениях х,
- 4. Рассмотрим геометрический смысл этого определения.Неравенстворавносильно двойному неравенствучто соответствует расположению части графика у=f(x) в полосе шириной 2ε.
- 6. Т.е. число А есть предел функции какой
- 7. Доказать, чтоПример.
- 8. Т.е. для любого ε >0 существует число
- 9. Рассмотренное определение предела при x стремящемся к
- 10. В случае, когда неравенстводолжно выполняться при всех
- 11. Число А называется пределом функции у=f(x), при
- 12. При всех значениях х, достаточно близкихк x0,
- 13. Неравенстворавносильно двойному неравенствуАналогично неравенстворавносильно неравенствуЭто соответствует расположению
- 14. Т.е. число А есть предел функции при
- 16. Доказать, чтоПример.
- 17. Пусть ε=0.1Тогда неравенство будет выполняться при Аналогично, при ε=0.01Неравенство будет выполняться приРешение.
- 18. Т.е. для любого ε >0 неравенствовыполняется приТ.е.
- 19. Определение предела не требует существования функции в
- 20. переменная x принимает значения только меньше x0
- 21. Определение этих пределов будет аналогично рассмотренному выше
- 22. Скачать презентацию
- 23. Похожие презентации
Число А называется пределом функции у=f(x), при х стремящемся к бесконечности, если для любого, сколь угодно малого числа ε>0, найдется такое положительное числоS, что при всех |x|>S, выполняетсянеравенство:
Слайд 2
Число А называется пределом функции
у=f(x), при х
стремящемся к бесконечности,
числаε>0, найдется такое положительное число
S, что при всех |x|>S, выполняется
неравенство:
Слайд 3
При достаточно больших по модулю значениях
х, значения
функции f(x) очень мало
отличаются от числа А (меньше,
чем на число ε , каким бы малым оно не было).
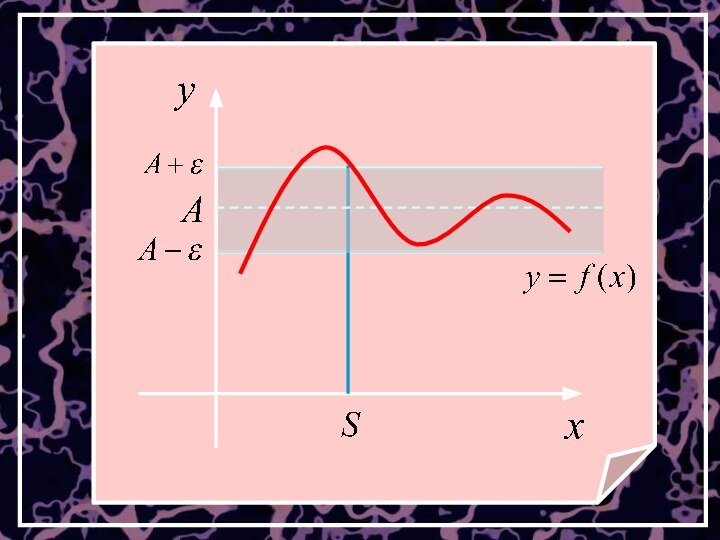
смысл определения:
Слайд 4
Рассмотрим геометрический смысл этого определения.
Неравенство
равносильно двойному неравенству
что соответствует
расположению части графика у=f(x) в полосе шириной 2ε.
Слайд 6
Т.е. число А есть предел функции
какой бы
узкой она не была.
если для любого, сколь угодно
малого числа ε>0, найдется такое число S, что при всехсоответствующие ординаты графика функции у=f(x) будут заключены в полосе
Слайд 8
Т.е. для любого ε >0 существует число
Такое,
что для всех х, таких что |x|>S, выполняется неравенство:
Для
любого ε>0Решение.
Слайд 9 Рассмотренное определение предела при x стремящемся к бесконечности
предполагает неограниченное возрастание x по абсолютной величине.
Можно сформулировать понятие
предела при стремлении x к бесконечности любого знака, т.е. при Замечание 1.
Слайд 10
В случае, когда
неравенство
должно выполняться при всех x
таких, что х>s.
В случае, когда
неравенство
должно выполняться при всех
x таких, что х<-s.Перейдем к понятию предела функции в точке.
Рассмотрим некоторую функцию у=f(x). Пусть эта функция задана в некоторой окрестности точки x0, кроме, может быть, самой этой точки.
Слайд 11
Число А называется пределом функции
у=f(x), при х→x0,
(или в точке x0)
если для любого, сколь угодно малого
числа ε>0, найдется такое положительное число
δ, что при всех |x-x0|< δ, выполняется
неравенство:
Слайд 12
При всех значениях х, достаточно близких
к x0, значения
функции у=f(x) очень мало
отличаются по абсолютной величине
от
числа А (меньше, чем на число ε, каким бы малым оно не было).
смысл определения:
Слайд 13
Неравенство
равносильно двойному неравенству
Аналогично неравенство
равносильно неравенству
Это соответствует расположению части
графика
в полосе шириной 2ε и попаданию точки х в
δ -окрестность точки x0.
Слайд 14
Т.е. число А есть предел функции
при х→x0,
если для любого, сколь угодно малого
числа
какой бы узкой
она не была. найдется такая δ–окрестность точки x0, что для всех х≠x0 из этой окрестности соответствующие ординаты графика функции
будут заключены в полосе
Слайд 17
Пусть ε=0.1
Тогда неравенство
будет выполняться при
Аналогично, при
ε=0.01
Неравенство будет выполняться при
Решение.
Слайд 18
Т.е. для любого ε >0 неравенство
выполняется при
Т.е. для
любого ε >0 существует число
что для всех х,
таких что |x-1|<δ, выполняется неравенство:Слайд 19 Определение предела не требует существования функции в самой
точке x0, т.к. рассматриваются значения функции в некоторой окрестности
точки x0.Т.е. рассматривая предел
мы предполагаем, что
но не достигает значения x0.
Замечание 2.
Слайд 20 переменная x принимает значения только меньше x0 или,
наоборот, больше x0, и при этом функция f(x) стремится
к некоторому числу А, то говорят об односторонних пределах соответственно справа и слева:Если при
Замечание 3.
Слайд 21 Определение этих пределов будет аналогично рассмотренному выше при
Вместо значений x, удовлетворяющих условию
рассматриваются такие x, что
при
и значения x, такие что
при
