Презентация на тему Преобразование графиков

ОХ
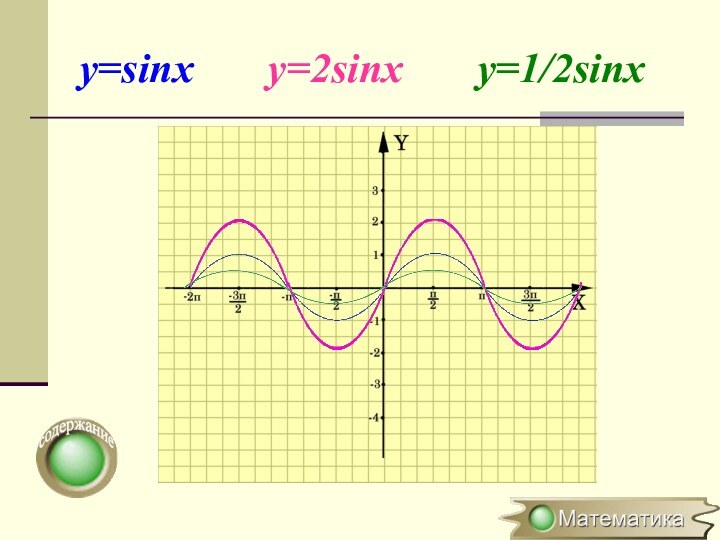
Растяжение (сжатие) в k раз вдоль оси OY
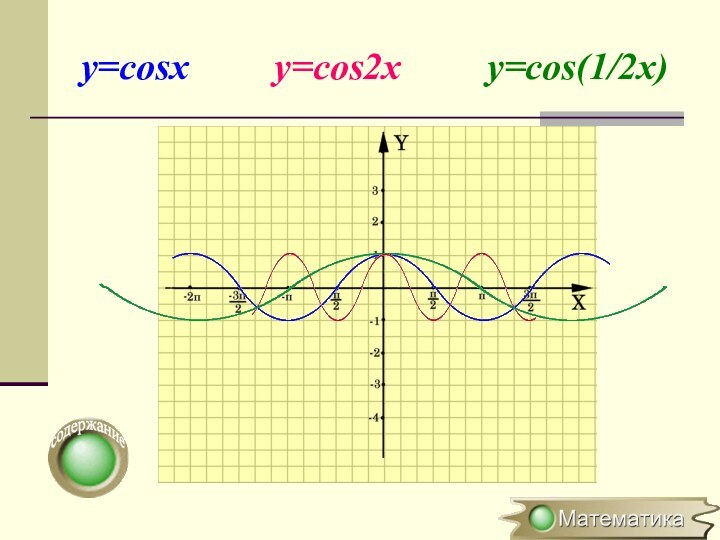
Растяжение (сжатие)

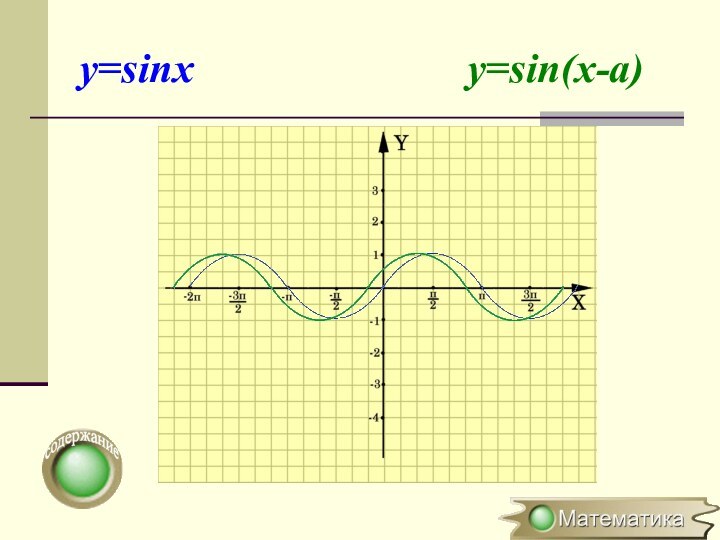
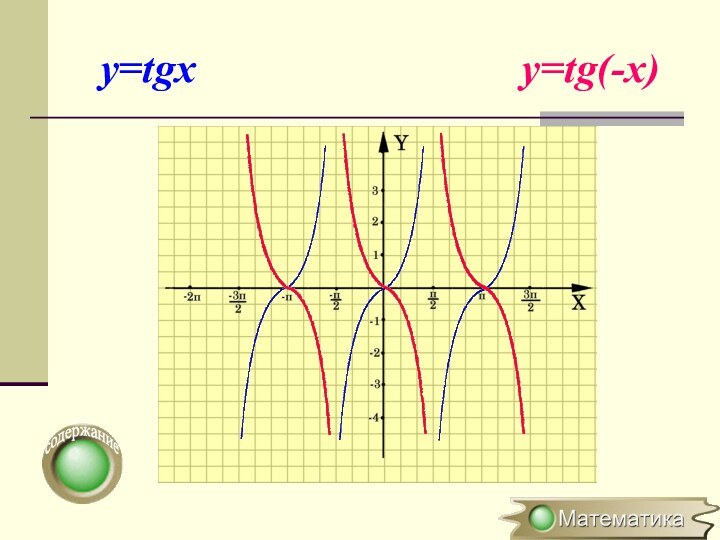
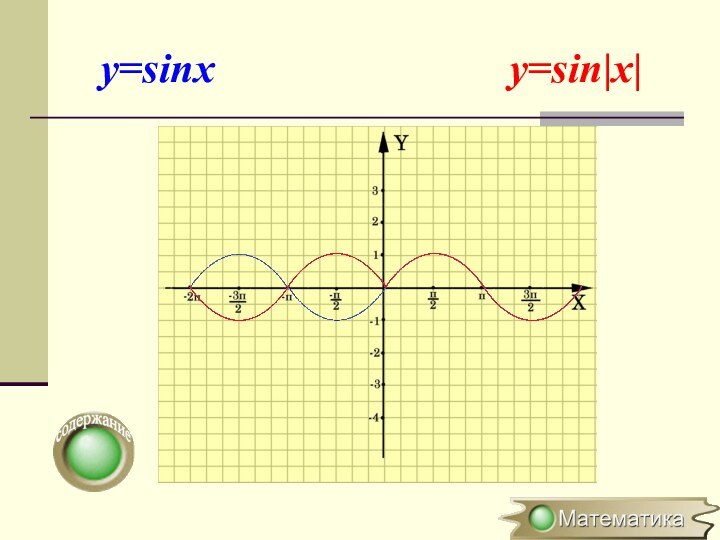
в k раз вдоль оси OХ
Симметричное отображение относительно оси OY
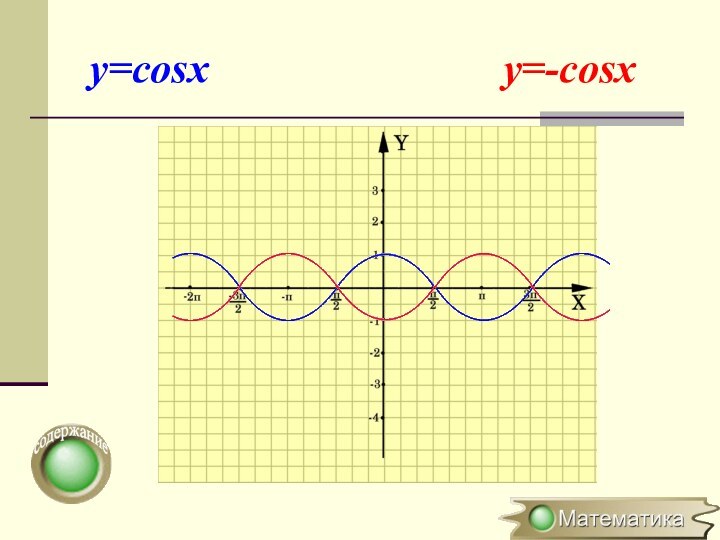
Симметричное отображение относительно оси OX
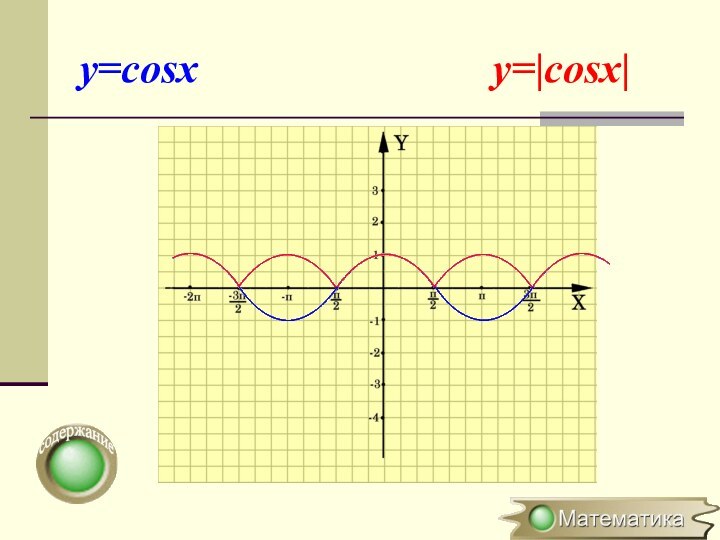
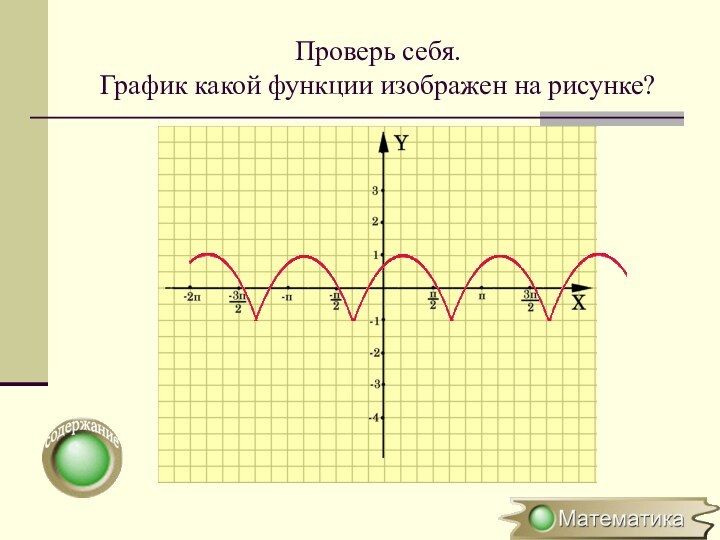
Построение графика y=|f(x)|
Построение графика y=f(|x|)

OY
y=f(x) → y=f(x)+a

(x0;y0) → (x0;y0+a)

Для построения графика функции y=f(x)+a необходимо график функции y=f(x) перенести вдоль оси OY на вектор (0;а)

y=sin x+2

y=f(x) → y=f(x-a)
(x0;y0)

→ (x0+a;y0)

Для построения графика функции y=f(x-a) необходимо график функции y=f(x) перенести вдоль оси OX на вектор (0;а)

y=sin(x-a)

y=f(x) → y=kf(x), где k>0

(x0;y0) → (x0;ky0)

Для построения графика функции y=kf(x) необходимо график функции y=f(x) растянуть в k раз вдоль оси ОY для k >1 или сжать в 1/k развдоль оси OY для k<1

y=1/2sinx

y=f(x) → y=f(kx), где k>0

(x0;y0) → ( x0;y0)

Для построения графика функции y=f(kx) необходимо график функции y=f(x) сжать в k раз вдоль оси ОХ для k >1 или растянуть в 1/k раз вдоль оси OХ для k<1

y=cos(1/2x)

y=-f(x)
(x0;y0) → (x0;-y0)


Для построения

графика функции y=-f(x) необходимо график функции y=f(x)симметрично отобразить относительно оси ОХ

y=-cosx

→ y=f(-x)
(x0;y0) → (-x0;y0)


Для построения

графика функции y=f(-x) необходимо график функции y=f(x) симметрично отобразить относительно
оси ОY

y=tg(-x)

y=|f(x)| необходимо часть графика функции y=f(x), лежащую выше оси

OX, оставить неизменной, а часть графика y=f(x), лежащую ниже оси OХ, симметрично отобразить относительно оси ОХ

f(x), если х 0
y=|f(x)|=
-f(x), если х < 0

y=|cosx|

f(x), если х 0
y=f(|x|)=
f(-x), если х<0


Для построения графика функции y=|f(x)| необходимо часть графика функции y=f(x), лежащую правее оси OY, оставить неизменной, а часть графика y=f(x), лежащую левее оси OY, симметрично отобразить относительно оси ОY

y=sin|x|