= f(x) - a
+a
-a
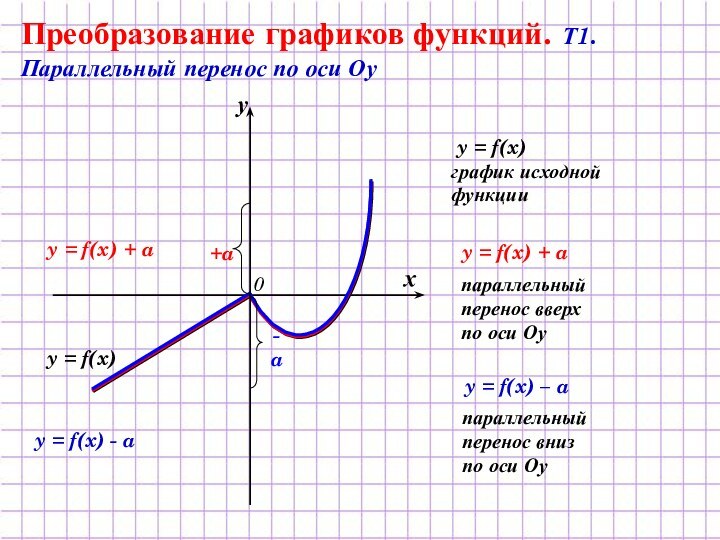
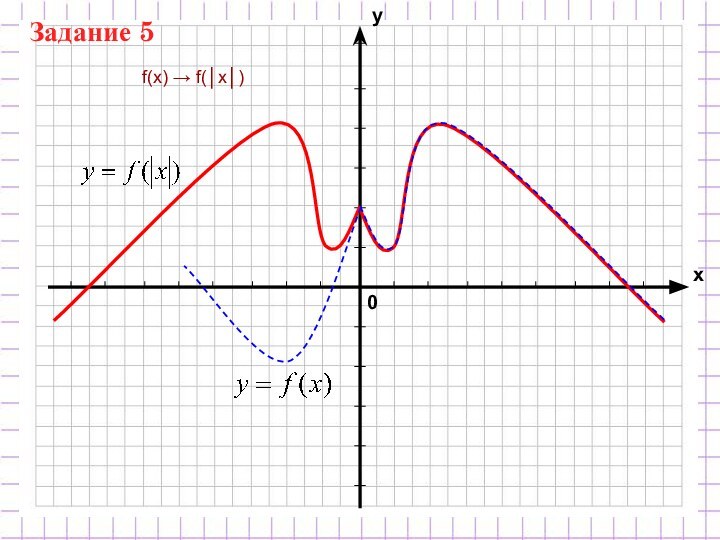
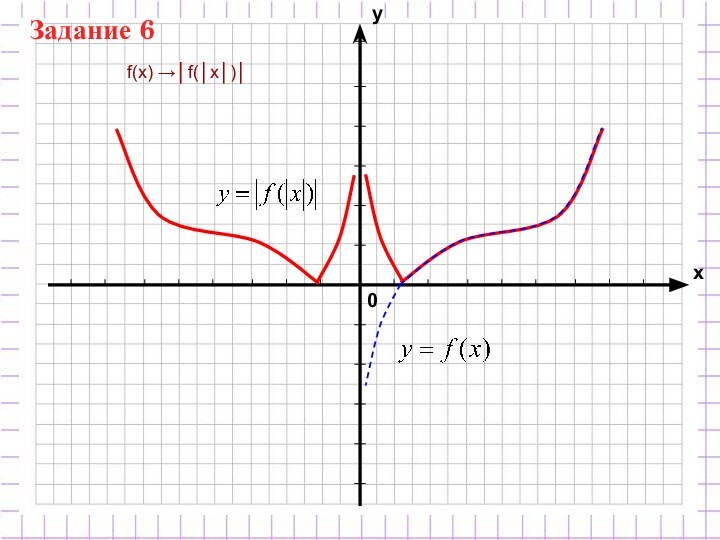
Преобразование графиков функций. Т1. Параллельный перенос
по оси Оу y = f(x)
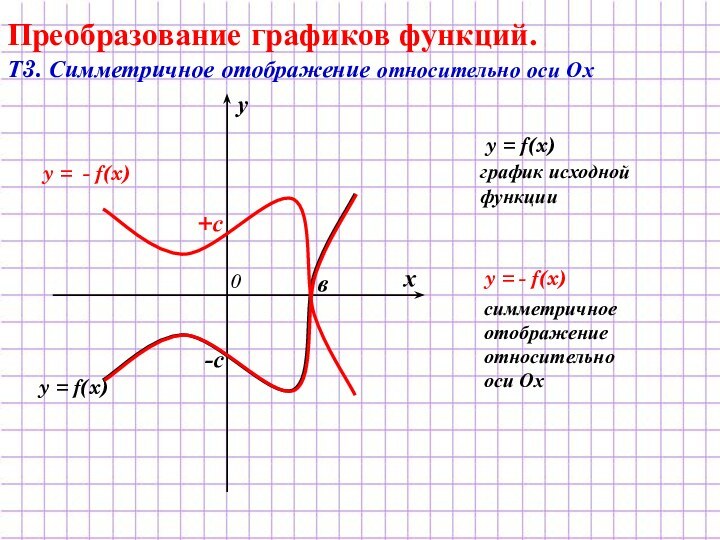
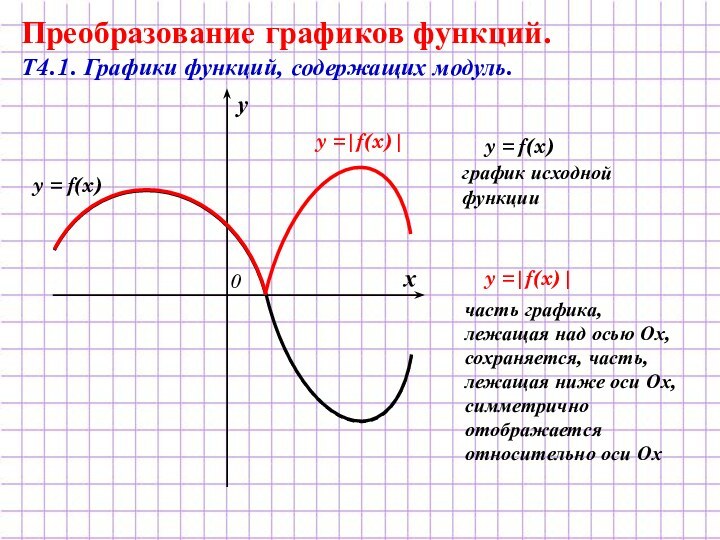
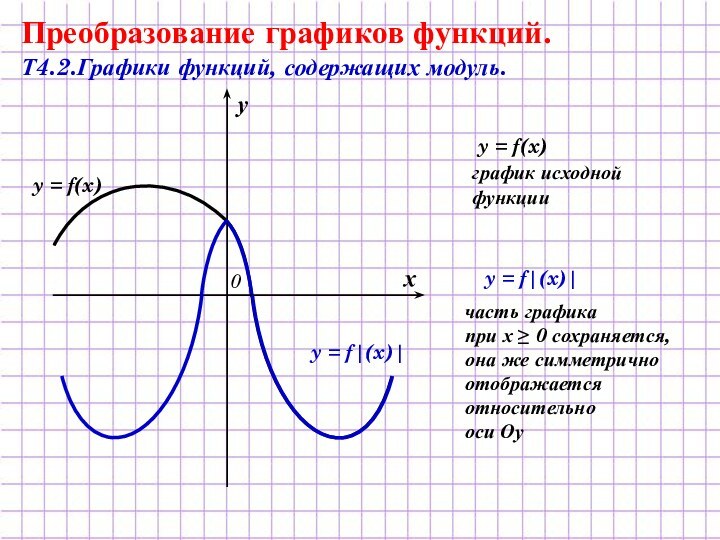
график исходной
функции
y = f(x) + a
y = f(x) – a
параллельный
перенос вверх
по оси Оу
параллельный
перенос вниз
по оси Оу
х
у
0