Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Преобразование графиков тригонометрических функций

Содержание

y = cos(x+2)y=cos2xy=sinx +2y=-3cosxy=sin1/2xy=sin(x-5)y=tg2xy=2ctgxy=ctg1/3xy=1/3sinxy=4-cosxy=ctgx+1Сгруппируйте функции по какому-нибудь признакуy=-tgx
Преобразование графиков тригонометрических функций y = cos(x+2)y=cos2xy=sinx +2y=-3cosxy=sin1/2xy=sin(x-5)y=tg2xy=2ctgxy=ctg1/3xy=1/3sinxy=4-cosxy=ctgx+1Сгруппируйте функции по какому-нибудь признакуy=-tgx изменение функцииизменение аргумента Построить графики функции y=cosxy=cos2xy=cos1/2x y=cosxy=cos2xy=cos1/2x Построить графики функции y=sinxy=sin(x+2)y=sin(x-2) y=sinxy=sin(x+2)y=sin(x-2) Определите периоды функции y=cos2xy=sin(x-2)y=cos1/2xy=sin(x+2)y=cosxy=sinxТ=2πТ=πТ=4πТ=2πТ=2πТ=2π Построить графики функции y=2cosxy=1/2cosxy=-cosx y=cosxy=2cosxy=1/2cosxпостроить график y=cosx2. увеличить ординату в 2 раза период Т=2πпостроить график y=sinxy=sinx+2y=sinx-2 y=sinxy=sinx+2y=sinx-2построить график y=sinxсдвинуть график на 2 единицы вверх по оси ОYпостроить график Исследуем графики функции y=cos2xy=cos1/2x Свойства функции:D(y)=R; E(y)=[-1;1];Период: π ; Свойства функции:D(y)=R; E(y)=[-1;1];Период: 4π ; Исследуем графики функции y=2-2cosxy=1/2sinx+1 Свойства функции:D(y)=R; E(y)=[0;4];Период: 2π ; Свойства функции:D(y)=R; E(y)=[0,5;3,5];Период: 2π ; Выводы: y=sin xy=sin(x+1.7)+2y=sin(x-1.7)-2
Слайды презентации

Слайд 2 y = cos(x+2)
y=cos2x
y=sinx +2
y=-3cosx
y=sin1/2x
y=sin(x-5)
y=tg2x
y=2ctgx
y=ctg1/3x
y=1/3sinx
y=4-cosx
y=ctgx+1
Сгруппируйте функции по какому-нибудь признаку
y=-tgx

y = cos(x+2)y=cos2xy=sinx +2y=-3cosxy=sin1/2xy=sin(x-5)y=tg2xy=2ctgxy=ctg1/3xy=1/3sinxy=4-cosxy=ctgx+1Сгруппируйте функции по какому-нибудь признакуy=-tgx

Слайд 3 изменение функции
изменение аргумента

изменение функцииизменение аргумента

Слайд 4 Построить графики функции
y=cosx
y=cos2x
y=cos1/2x

Построить графики функции y=cosxy=cos2xy=cos1/2x

Слайд 5

Слайд 6 y=cosx
y=cos2x
y=cos1/2x

y=cosxy=cos2xy=cos1/2x

Слайд 7 Построить графики функции
y=sinx
y=sin(x+2)
y=sin(x-2)

Построить графики функции y=sinxy=sin(x+2)y=sin(x-2)

Слайд 8

Слайд 9 y=sinx
y=sin(x+2)
y=sin(x-2)

y=sinxy=sin(x+2)y=sin(x-2)

Слайд 10 Определите периоды функции
y=cos2x
y=sin(x-2)
y=cos1/2x
y=sin(x+2)
y=cosx
y=sinx
Т=2π
Т=π
Т=4π
Т=2π
Т=2π
Т=2π

Определите периоды функции y=cos2xy=sin(x-2)y=cos1/2xy=sin(x+2)y=cosxy=sinxТ=2πТ=πТ=4πТ=2πТ=2πТ=2π

Слайд 11 Построить графики функции
y=2cosx
y=1/2cosx
y=-cosx

Построить графики функции y=2cosxy=1/2cosxy=-cosx

Слайд 12

Слайд 13 y=cosx
y=2cosx
y=1/2cosx
построить график y=cosx
2. увеличить ординату в 2

y=cosxy=2cosxy=1/2cosxпостроить график y=cosx2. увеличить ординату в 2 раза период Т=2πпостроить график

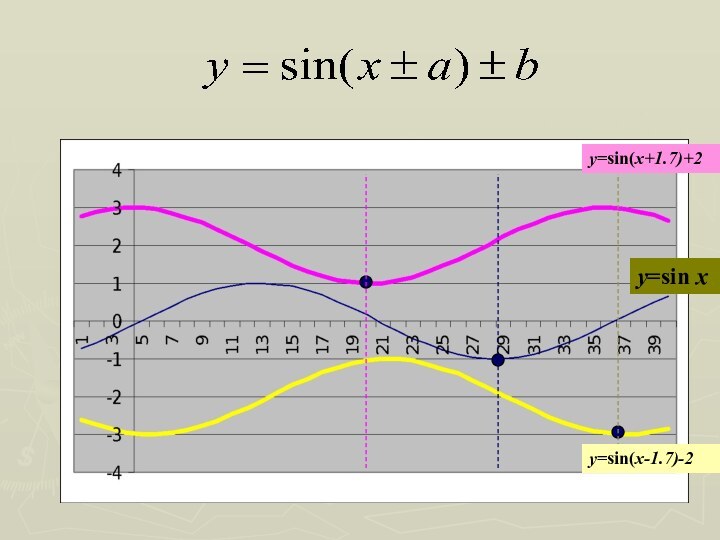
раза
период Т=2π
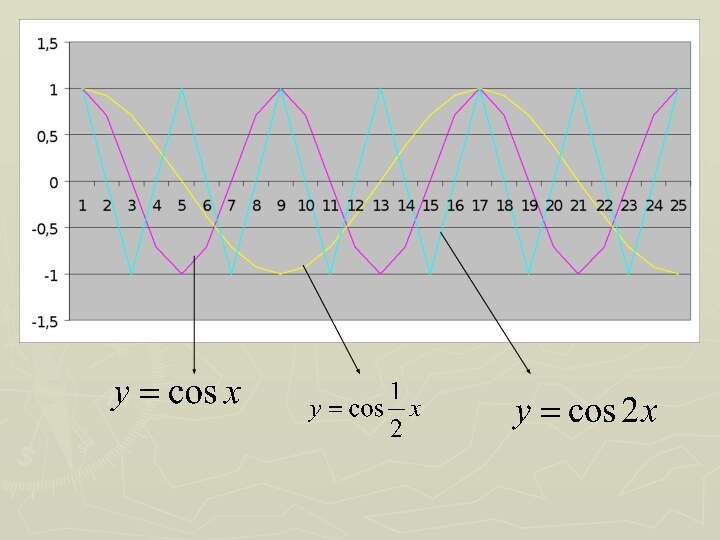
построить график y=cosx

2. уменьшить ординату в 2

раза

период Т=2π

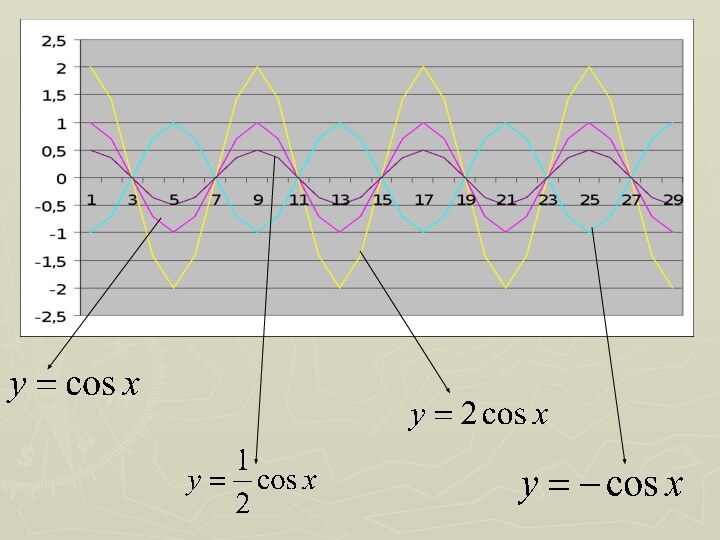
y=-cosx

построить график y=cosx
Выполнить зеркальное отображение относительно оси ОХ

Слайд 14 y=sinx
y=sinx+2
y=sinx-2

y=sinxy=sinx+2y=sinx-2

Слайд 15

Слайд 16 y=sinx
y=sinx+2
y=sinx-2
построить график y=sinx
сдвинуть график на 2 единицы вверх

y=sinxy=sinx+2y=sinx-2построить график y=sinxсдвинуть график на 2 единицы вверх по оси ОYпостроить

по оси ОY

построить график y=sinx
2. сдвинуть график на 2

единицы вниз по оси ОY

период Т=2π

период Т=2π

Слайд 17 Исследуем графики функции
y=cos2x
y=cos1/2x

Исследуем графики функции y=cos2xy=cos1/2x

Слайд 18 Свойства функции:
D(y)=R; E(y)=[-1;1];
Период:

Свойства функции:D(y)=R; E(y)=[-1;1];Период: π ; Четная;Возрастает: [-π/2+πn;πn]Убывает: [πn;π/2+πn]Нули функции:(π/4+1/2πn;0)Точки max: πn;Точки min: π/2+πn;y=cos2x

π ; Четная;
Возрастает: [-π/2+πn;πn]
Убывает: [πn;π/2+πn]
Нули функции:(π/4+1/2πn;0)
Точки

max: πn;
Точки min: π/2+πn;

y=cos2x

Слайд 19 Свойства функции:
D(y)=R; E(y)=[-1;1];
Период:

Свойства функции:D(y)=R; E(y)=[-1;1];Период: 4π ; Четная;Возрастает: [-2π+4πn;4πn] Убывает:

4π ; Четная;
Возрастает: [-2π+4πn;4πn]
Убывает: [4πn;2π+4πn]
Нули

функции:(π+2πn;0)
Точки max: 4πn;
Точки min: 2π+4πn;

y=cos1/2x

Слайд 20 Исследуем графики функции
y=2-2cosx
y=1/2sinx+1

Исследуем графики функции y=2-2cosxy=1/2sinx+1

Слайд 21 Свойства функции:
D(y)=R; E(y)=[0;4];
Период:

Свойства функции:D(y)=R; E(y)=[0;4];Период: 2π ; Четная;Возрастает: [2πn;π+2πn]Убывает: [π+2πn;2π+2πn]Нули функции:(2πn;0)Точки max: π+2πn;Точки min: 2πn;y=2-2cosx

2π ; Четная;
Возрастает: [2πn;π+2πn]
Убывает: [π+2πn;2π+2πn]
Нули функции:(2πn;0)
Точки

max: π+2πn;
Точки min: 2πn;

y=2-2cosx

Слайд 22 Свойства функции:
D(y)=R; E(y)=[0,5;3,5];
Период:

Свойства функции:D(y)=R; E(y)=[0,5;3,5];Период: 2π ; Четная;Возрастает: [-π/2+2πn; π/2+2πn]

2π ; Четная;
Возрастает: [-π/2+2πn; π/2+2πn]
Убывает:

[π/2+2πn; 3π/2+2πn]
Нули функции:--------
Точки max: π/2+2πn;
Точки min: -π/2+2πn;

y=1/2sinx+1

Слайд 23 Выводы:

Выводы:

Слайд 24

  • Имя файла: preobrazovanie-grafikov-trigonometricheskih-funktsiy.pptx
  • Количество просмотров: 126
  • Количество скачиваний: 0
- Предыдущая Еда и ее значение
Следующая - Авторское право в законодательстве

Похожие презентации

Игры и игровые упражнения как средство формирования ЭМП у детей старшего дошкольного возраста. презентация к занятию по математике (подготовительная группа) Игры и игровые упражнения как средство формирования ЭМП у детей старшего дошкольного возраста. презентация к занятию по математике (подготовительная группа) 54
ПНШ 4 класс урок математики Учимся решать задачи с помощью уравнений план-конспект урока по математике (4 класс) ПНШ 4 класс урок математики Учимся решать задачи с помощью уравнений план-конспект урока по математике (4 класс) 213
Сравнение многозначных чисел Сравнение многозначных чисел 124
Отношения и пропорции. (6 класс) Отношения и пропорции. (6 класс) 131
Сложение чисел с разными знаками Сложение чисел с разными знаками 139
Урок-общественный смотр значений по математике Урок-общественный смотр значений по математике 121
Презентация к уроку Состав числа 10 презентация к уроку по математике (1 класс) Презентация к уроку Состав числа 10 презентация к уроку по математике (1 класс) 117
Сложение и вычитание десятичных дробей Сложение и вычитание десятичных дробей 95
Картотека дидактических игр по ФЭМП картотека по математике (старшая группа) Картотека дидактических игр по ФЭМП картотека по математике (старшая группа) 143
Уравнения и неравенства Уравнения и неравенства 105
Презентация по математике контрольная работа №1 (6 класс) Презентация по математике контрольная работа №1 (6 класс) 117
Устный счёт презентация к уроку по математике (3 класс) Устный счёт презентация к уроку по математике (3 класс) 103
Признаки делимости Признаки делимости 108
Древние меры длины презентация к уроку по математике (старшая группа) Древние меры длины презентация к уроку по математике (старшая группа) 125
Степенная функция и ее свойства Степенная функция и ее свойства 136
Интерактивная игра- тренажёр Озорная гусеница по теме Сложение и вычитание в пределах 10 Интерактивная игра- тренажёр Озорная гусеница по теме Сложение и вычитание в пределах 10 39
Презентация материал по математике (1 класс) по теме Презентация материал по математике (1 класс) по теме 113
Урок математики в 1 классе Число 9. Цифра 9 план-конспект урока по математике (1 класс) Урок математики в 1 классе Число 9. Цифра 9 план-конспект урока по математике (1 класс) 116
Презентация Час. Минута. Определение времени по часам. презентация к уроку по математике (2 класс) Презентация Час. Минута. Определение времени по часам. презентация к уроку по математике (2 класс) 262
Презентация Способы прибавления и вычитания числа 4 презентация к уроку (математика, 1 класс) по теме Презентация Способы прибавления и вычитания числа 4 презентация к уроку (математика, 1 класс) по теме 55
Математический диктант Математический диктант 129
Внеклассное мероприятие В гостях у Пифагора и Роберта Гука Внеклассное мероприятие В гостях у Пифагора и Роберта Гука 150
polyot v kosmos polyot v kosmos 140
Скалярное произведение векторов Скалярное произведение векторов 89
Делим на части презентация к уроку по математике (2 класс) Делим на части презентация к уроку по математике (2 класс) 52
Презентация по математике на тему Преобразование графиков функций Презентация по математике на тему Преобразование графиков функций 115
Дидактическая игра Ну-ка, зайка, сосчитай-ка! Игрушки Дидактическая игра Ну-ка, зайка, сосчитай-ка! Игрушки 41
Использование ИКТ презентация к уроку по математике (3 класс) Использование ИКТ презентация к уроку по математике (3 класс) 100
Презентация для образовательной ситуации по математическому развитию для детей средней группы Тема: Путешествие в страну великанов и лилипутов план-конспект занятия по математике (средняя группа) Презентация для образовательной ситуации по математическому развитию для детей средней группы Тема: Путешествие в страну великанов и лилипутов план-конспект занятия по математике (средняя группа) 125
Ю ю деп ужук Ю ю деп ужук 152