она применяется в тригонометрии?
Выпишите тригонометрические функции алгебраической суммы двух
аргументов (формулы сложения).3. Запишите мнемоническое правило запоминания формул сложения
4. Разберите и запишите в тетрадь решения примеров 1,2,3.
5. Выпишите формулы преобразования тригонометрических функций в алгебраическую сумму.
6. Разберите и запишите в тетрадь решение примера 4.
7. Выпишите формулы преобразования алгебраической суммы тригонометрических функций в произведение.
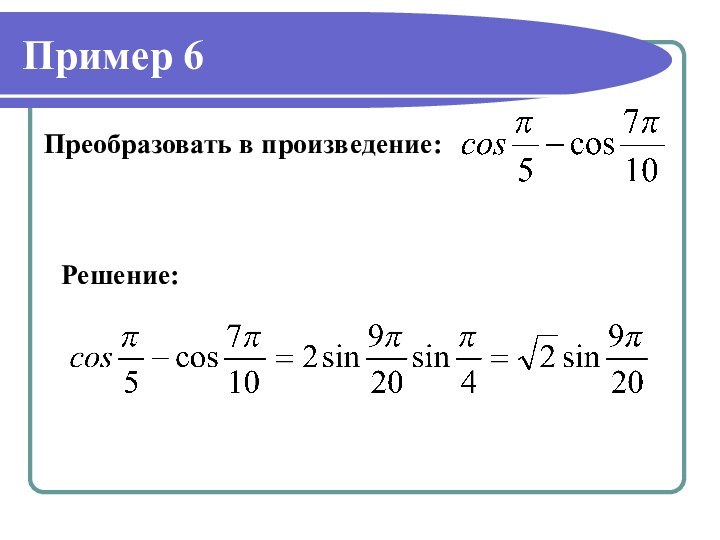
8. Разберите и запишите в тетрадь решения примеров 5,6.