- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Состав числа из двух меньших методическая разработка по математике (подготовительная группа)
Содержание
- 2. В старшем д/в стоит задача – изучение детьми состава чисел из единиц и двух меньших
- 3. Эта задача рассматривается как одна из наиболее важных в подготовке детей к вычислительной деятельности.ЗНАЧЕНИЕ:
- 4. операции с множествами предметов, создание множества из
- 5. осознание детьми того, как число может быть
- 6. дискретные величины, геометрические фигуры, предметы.МАТЕРИАЛ:
- 7. • постепенность (начинать с чисел 3, 4,5…),• не заучивать
- 8. Воспитатель выкладывает 5 кругов одного цвета, с
- 9. Медведица попросила медвежонка принести из леса 5
- 10. На 4 клумбах надо посадить по 5
- 11. У меня в двух руках 5
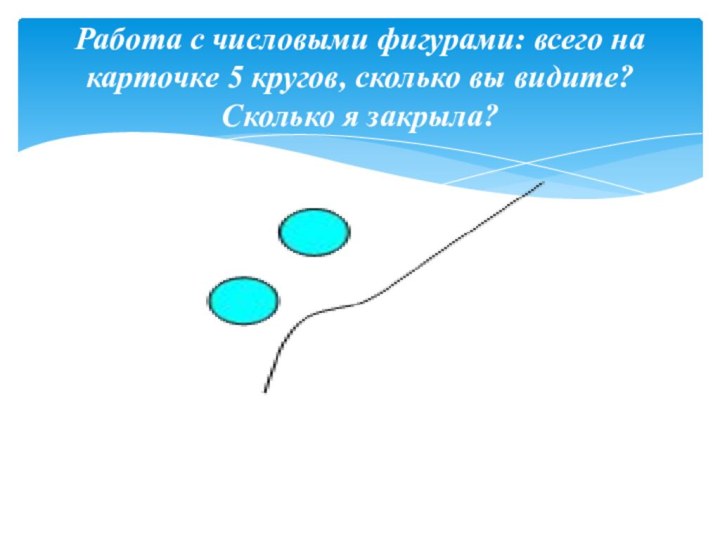
- 12. Работа с числовыми фигурами: всего на карточке 5 кругов, сколько вы видите? Сколько я закрыла?
- 13. Разделите 5 треугольников на две группы разными способами:
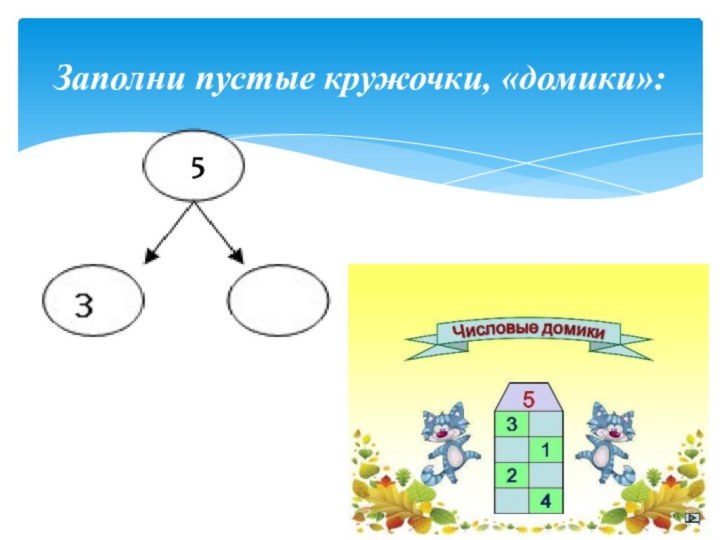
- 14. Заполни пустые кружочки, «домики»:5
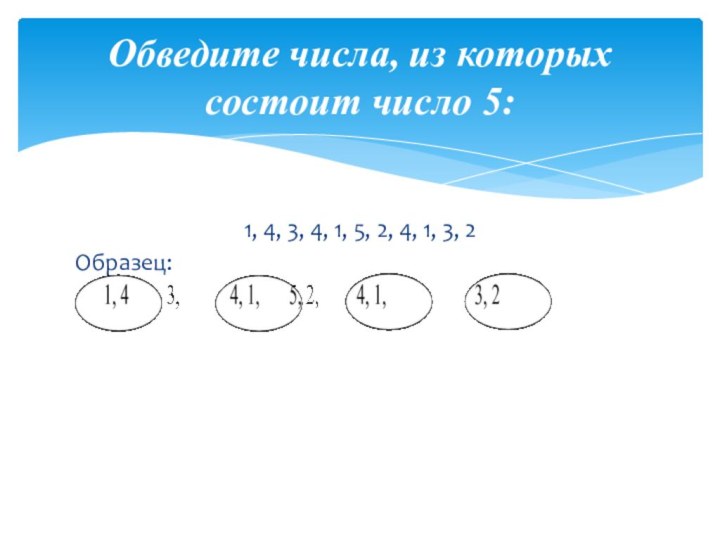
- 15. 1, 4, 3, 4, 1, 5, 2,
- 16. Разделить 5 карандашей между двумя детьми. Сколькими
- 17. Скачать презентацию
- 18. Похожие презентации
В старшем д/в стоит задача – изучение детьми состава чисел из единиц и двух меньших














Слайд 3 Эта задача рассматривается как одна из наиболее важных
в подготовке детей к вычислительной деятельности.
ЗНАЧЕНИЕ:
Слайд 4 операции с множествами предметов, создание множества из подмножества,
деление множеств на подмножества, сравнение их между собой.
ПОДГОТОВИТЕЛЬНАЯ РАБОТА:
Слайд 5 осознание детьми того, как число может быть образовано
из других чисел на основе анализа того, как множество
может быть образовано из частей.ОСНОВНАЯ ЦЕЛЬ:
Слайд 7
• постепенность (начинать с чисел 3, 4,5…),
• не заучивать состав,
а учить понимать способ действия,
• использовать предметные, символические, вербальные и
графические модели,• показать ВСЕ возможные варианты разложения числа на два меньших (по формуле n-1, где n – натуральное число).
ТРЕБОВАНИЯ:
Слайд 8 Воспитатель выкладывает 5 кругов одного цвета, с обратной
стороны круги имеют другой цвет (например, красный и синий).
Выяснить, сколько кругов, чем они похожи.Перевернуть первый круг, уточнить: сколько синих? сколько красных? сколько всего кругов? Сколько взяли синих и красных кругов, чтобы всего получилось 5? Выяснить, как получилось число 5:
1 да 4, 2 да 3, 3 да 2, 4 да 1
ПРИЕМЫ РАБОТЫ (для числа 5):





























