- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Применение производной к исследованию функции
Содержание
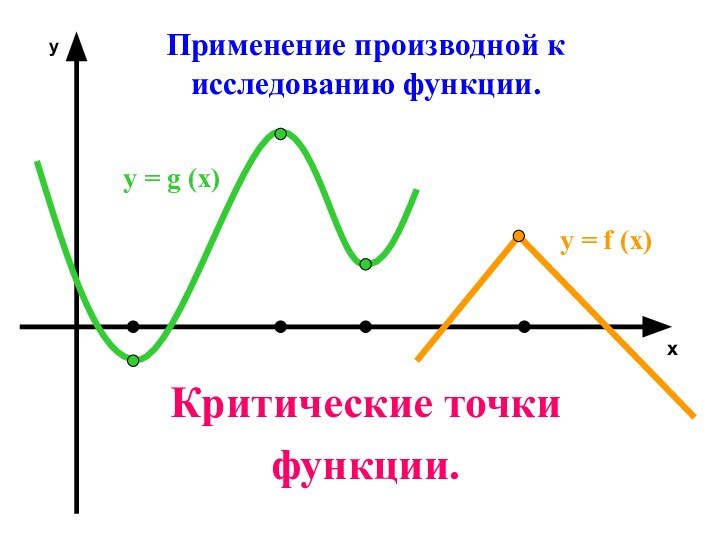
- 2. Применение производной к исследованию функции.Критические точкифункции.хуу = g (х)у = f (х)
- 3. Повторение: описание свойств функции по её
- 4. Повторение f(х)=…f(х)=…f(х)=…f(х)=…f(х)=…f(х)=…-20001
- 5. Постановка проблемыКак называются точки, в которых
- 6. 1. Точки экстремума. 1.1. Точки максимума.у =
- 7. 1. Точки экстремума.f(х1 ) > f (x)
- 8. 1. Точки экстремума.Точка х0 называется точкой минимума
- 9. 1. Точки экстремума.f(х4 ) < f (x)
- 10. 1. Точки экстремума. 1.3. Точки максимума и
- 11. 1. Точки экстремума. 1.4.хуу = f (х)
- 12. 2. Точки перегиба.хуу = х 30 у/
- 13. 3.Стационарные точки.Точки в которых производная функции равна
- 14. 4. Критические точки функции. у = |
- 15. 4. Критические точки функции. Внутренняя точка области
- 16. 5. Выполнение заданий.5.1. у = f (x)ху-2
- 17. 5. Выполнение заданий. 5.2.у = f (x)ху-2f
- 18. 5. Выполнение заданий.5.3.Найдите критические точки функции f(х)
- 19. 5. Выполнение заданий.5.4. 1. Функция определена для х ≠ 0 .
- 20. Итоги урока Точка минимума функцииТочка максимума функцииТочки
- 21. Скачать презентацию
- 22. Похожие презентации










Слайд 3
Повторение:
описание свойств функции по её графику
Изучение
нового материала:
точки экстремума функции
стационарные точки
функциикритические точки функции
~
~
~
~
Слайд 5
Постановка проблемы
Как называются точки,
в которых функция
«меняет характер»?
Как найти эти точки,
не выполняя
построения
графика
функции?
Слайд 6
1. Точки экстремума.
1.1. Точки максимума.
у = f
(х)
х
у
х1
х3
х2
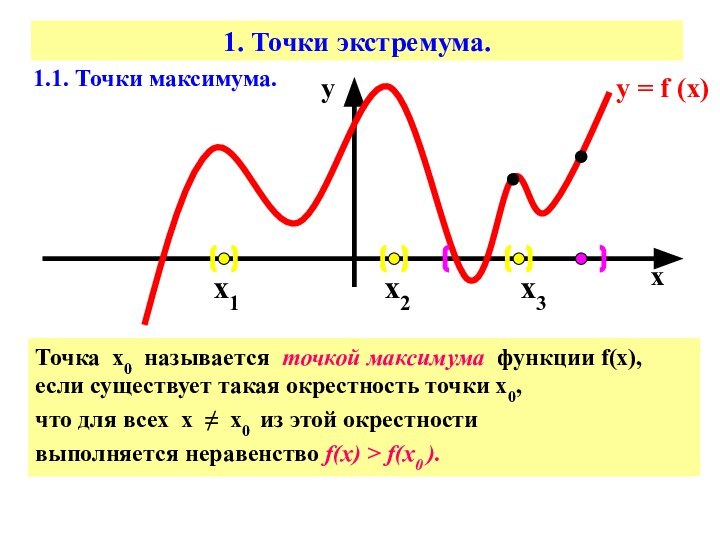
Точка х0 называется точкой максимума функции f(х), если
существует такая окрестность точки х0, что для всех х = х0 из этой окрестности
выполняется неравенство f(х) > f(х0 ).
Точка х0 называется точкой максимума функции f(х), если существует такая окрестность точки х0,
что для всех х ≠ х0 из этой окрестности
выполняется неравенство f(х) > f(х0 ).
Слайд 7
1. Точки экстремума.
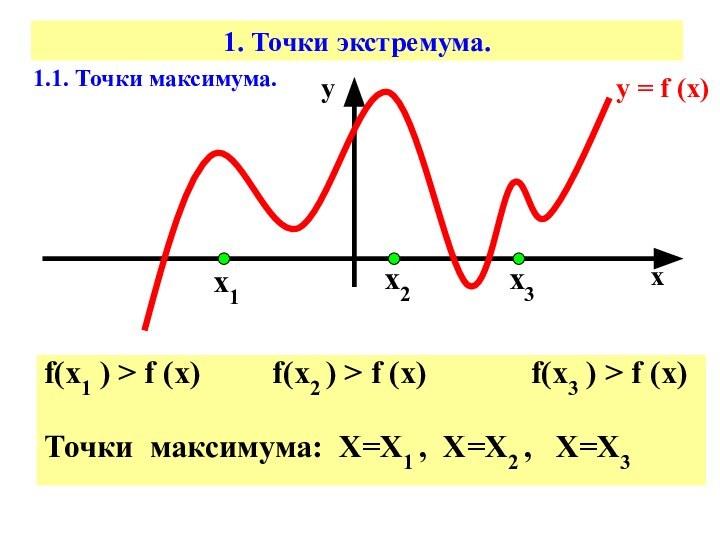
f(х1 ) > f (x)
f(x2 ) > f (x)
f(x3 ) > f (x)Точки максимума: Х=Х1 , Х=Х2 , Х=Х3
1.1. Точки максимума.
у = f (х)
х
у
х1
х3
х2
Слайд 8
1. Точки экстремума.
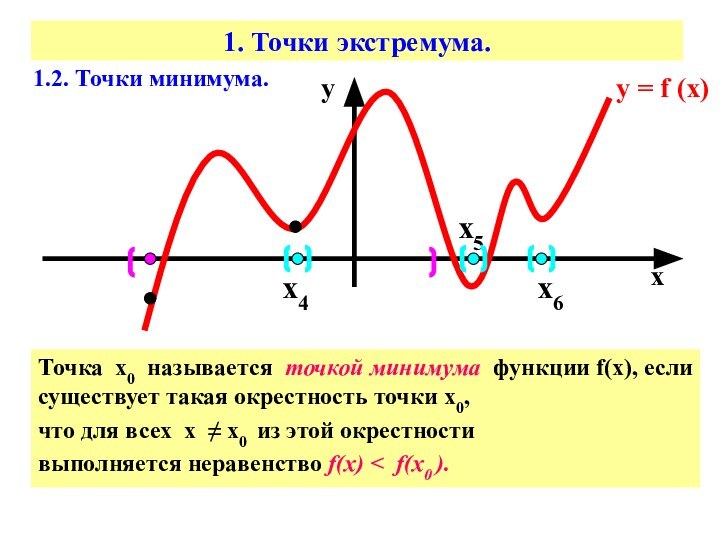
Точка х0 называется точкой минимума функции
f(х), если существует такая окрестность точки х0,
что для
всех х ≠ х0 из этой окрестности выполняется неравенство f(х) < f(х0 ).
1.2. Точки минимума.
у = f (х)
х
у
х4
х6
х5
Слайд 9
1. Точки экстремума.
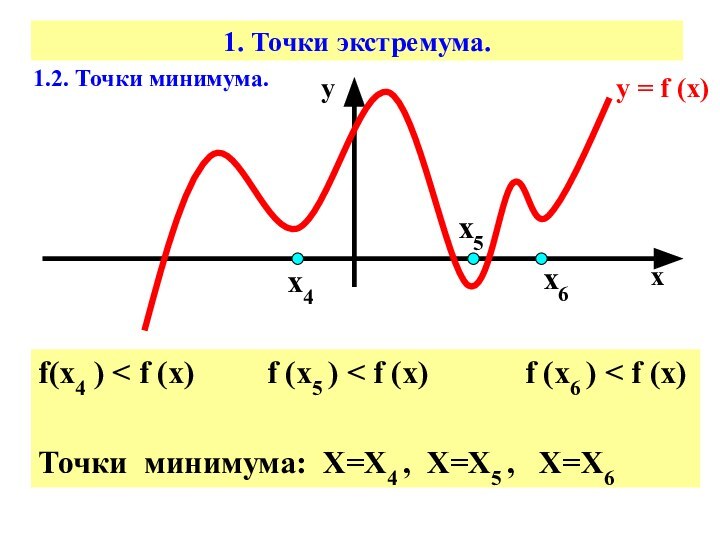
f(х4 ) < f (x)
f (x5 ) < f (x)
f (x6 ) < f (x)Точки минимума: Х=Х4 , Х=Х5 , Х=Х6
1.2. Точки минимума.
у = f (х)
х
у
х4
х6
х5
Слайд 10
1. Точки экстремума.
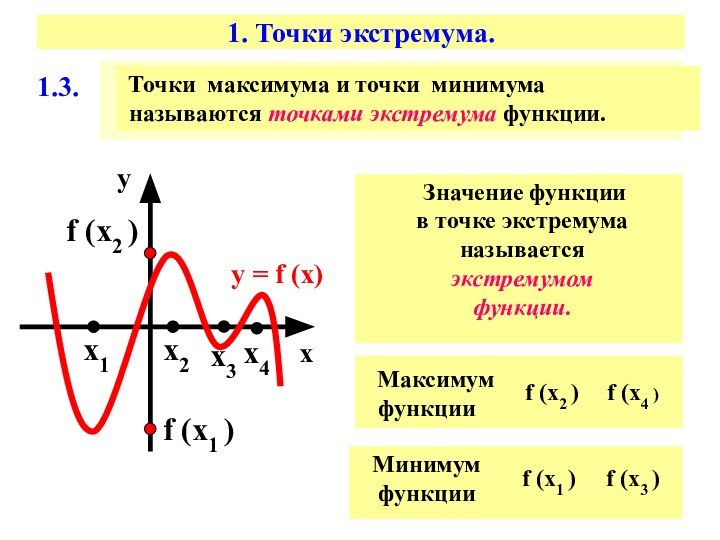
1.3.
Точки максимума и точки
минимума
называются точками экстремума функции.
х
у
у = f (х)
х1
х2
f (х1
)f (х2 )
Значение функции
в точке экстремума называется
экстремумом функции.
Максимум
функции
Минимум
функции
х3
х4
f (х2 )
f (х4 )
f (х1 )
f (х3 )
Слайд 11
1. Точки экстремума.
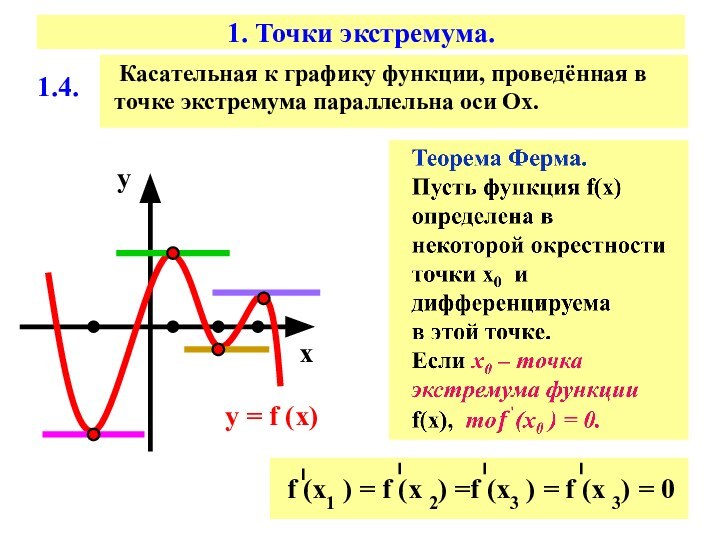
1.4.
х
у
у = f (х)
Касательная
к графику функции, проведённая в точке экстремума параллельна оси
Ох. f (x1 ) = f (x 2) =f (x3 ) = f (x 3) = 0
Слайд 12
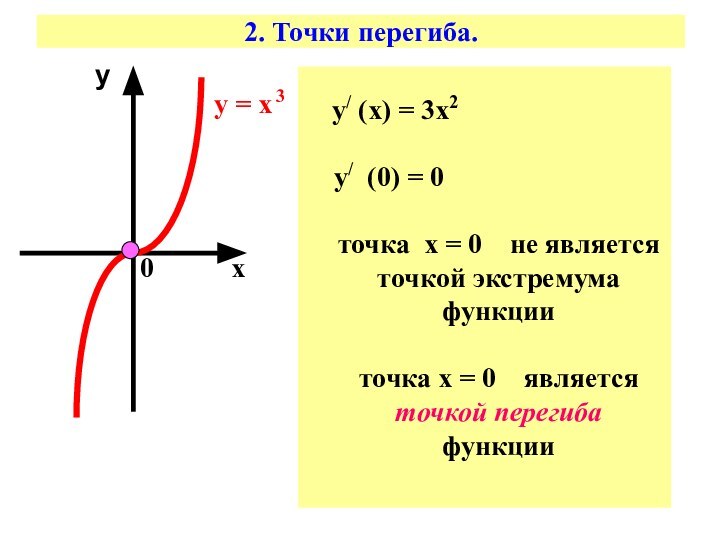
2. Точки перегиба.
х
у
у = х 3
0
у/ (х)
= 3х2
у/ (0) = 0
точка х = 0
не является точкой экстремумафункции
точка х = 0 является точкой перегиба
функции
Слайд 13
3.Стационарные точки.
Точки в которых производная функции равна нулю,
называются стационарными точками функции.
Точка максимума
Точка минимума
Точка перегиба
Стационарные
точки
Слайд 14
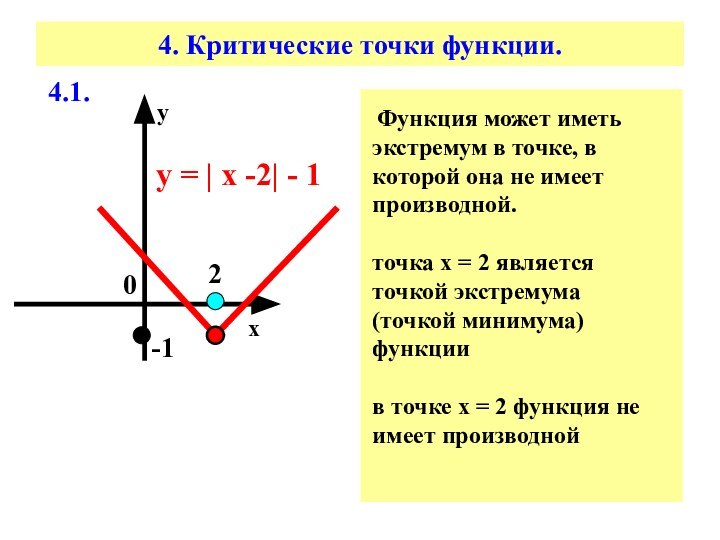
4. Критические точки функции.
у = | x
-2| - 1
х
у
0
-1
Функция может иметь экстремум в точке,
в которой она не имеет производной.точка х = 2 является точкой экстремума
(точкой минимума)
функции
в точке х = 2 функция не имеет производной
2
4.1.
Слайд 15
4. Критические точки функции.
Внутренняя точка
области определения
функции,
в которой эта функция имеет производную, равную нулю
или не имеет производной,
называется критической точкой этой функции.
4.2.
Слайд 16
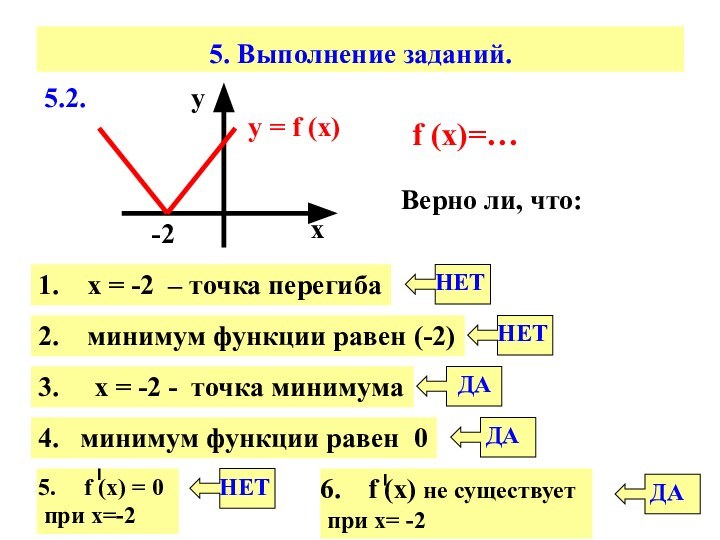
5. Выполнение заданий.
5.1.
у = f (x)
х
у
-2
0 2 4
х =
-2х = 0
х = 2
х = 4
точка минимума точка максимума
точка перегиба стационарная точка
критическая точка точка экстремума
Слайд 17
5. Выполнение заданий.
5.2.
у = f (x)
х
у
-2
f (x)=…
Верно
ли, что:
1. х = -2 – точка перегиба
2.
минимум функции равен (-2)3. х = -2 - точка минимума
4. минимум функции равен 0
f (х) = 0
при х=-2
f (х) не существует
при х= -2
НЕТ
НЕТ
НЕТ
ДА
ДА
ДА
Слайд 18
5. Выполнение заданий.
5.3.
Найдите критические точки функции f(х) =
х3+0,5х2– 4х
1. Функция определена для всех значений х.
2. Найдём
производную функции
f '(х) = 3х2+х– 4