с необходимостью решения ряда задач из физики, механики и
математики.Готфрид Вильгельм фон Лейбниц
Иcаак Ньютон
25 декабря 1642 — 20 марта 1727
1 июля 1646 — 14 ноября 1716,
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



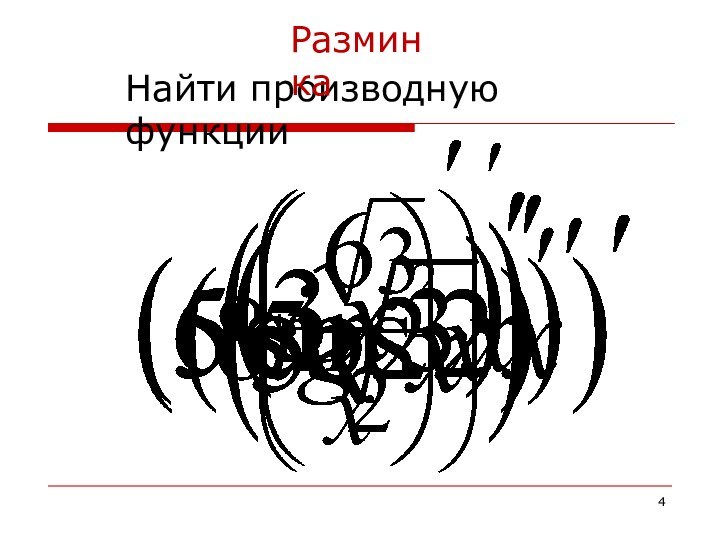





Готфрид Вильгельм фон Лейбниц
Иcаак Ньютон
25 декабря 1642 — 20 марта 1727
1 июля 1646 — 14 ноября 1716,
Комета Галлея вернется во внутреннюю Солнечную систему в следующий раз в 2061 году.
В 1705 году Эдмонд Галлей предсказал, что комета, которую наблюдали в 1531, 1607 и 1682 годах, должна возвратиться в 1758 году
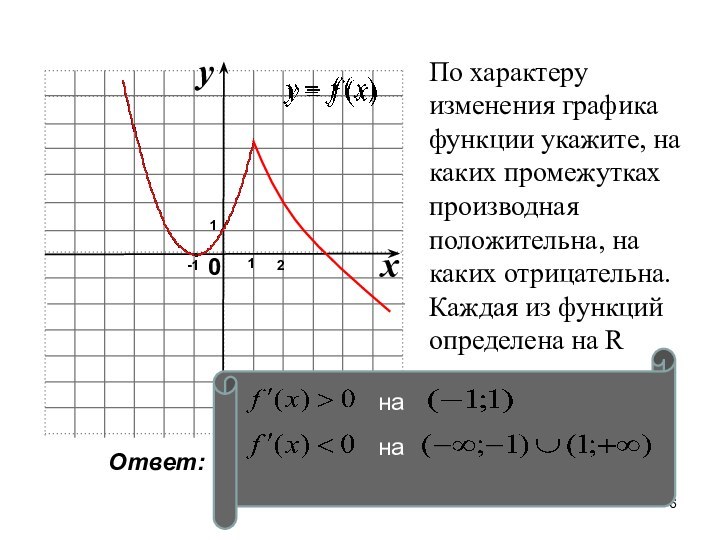
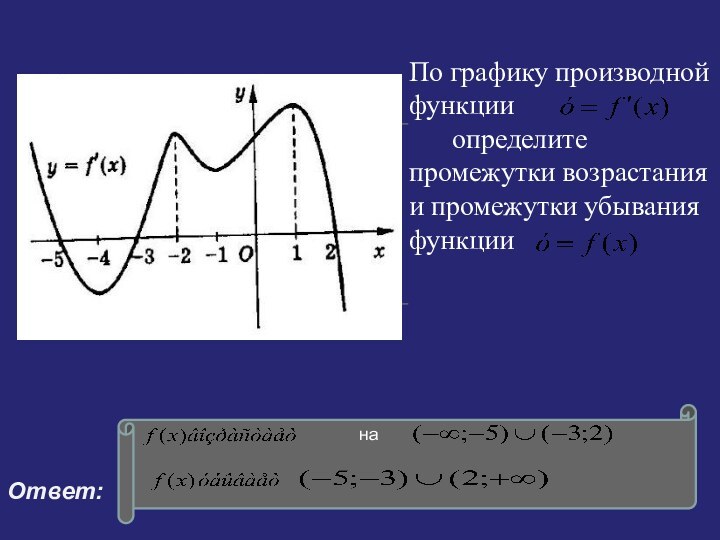
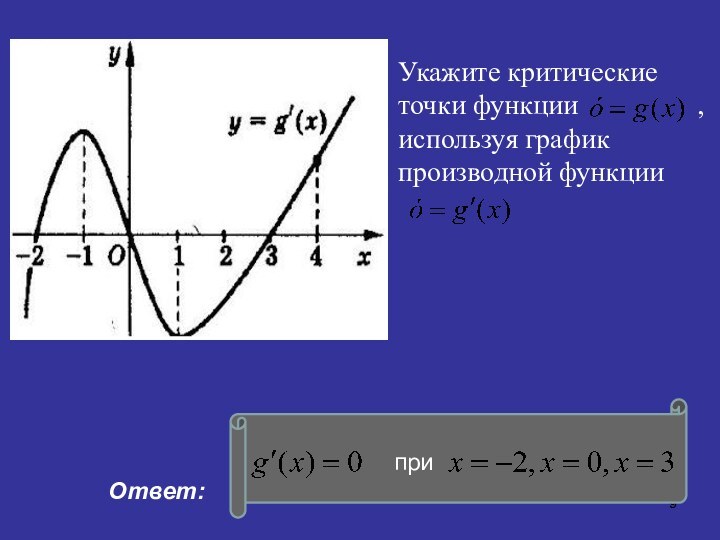
Ответ:
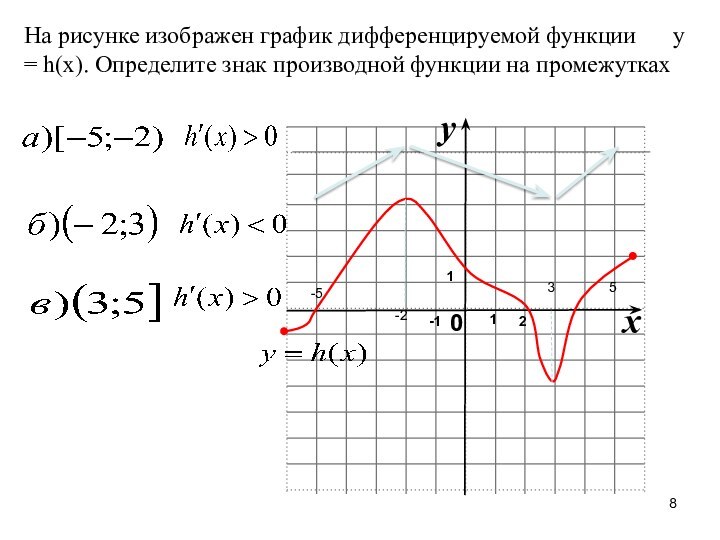
-2
3
-5
5
1
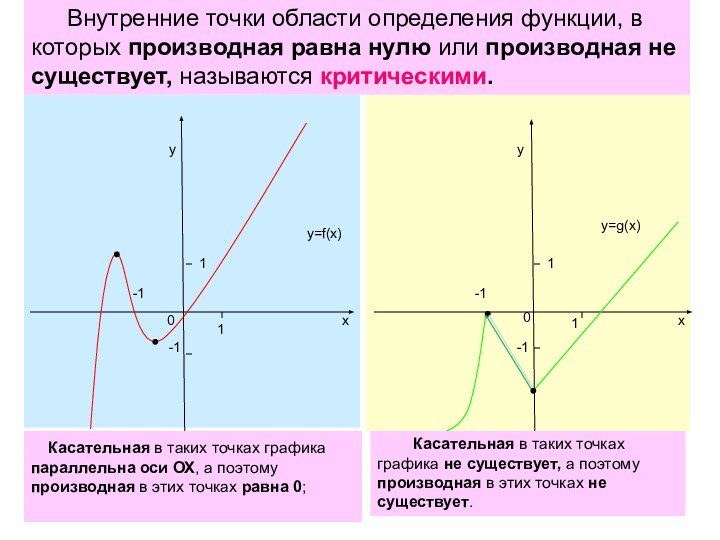
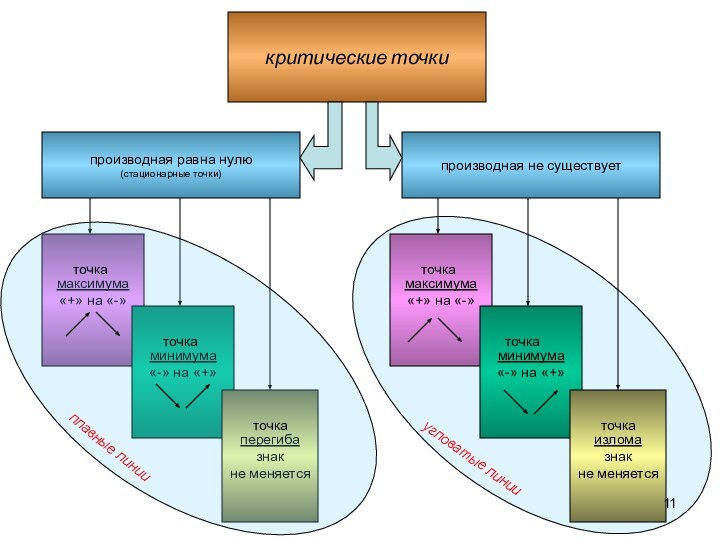
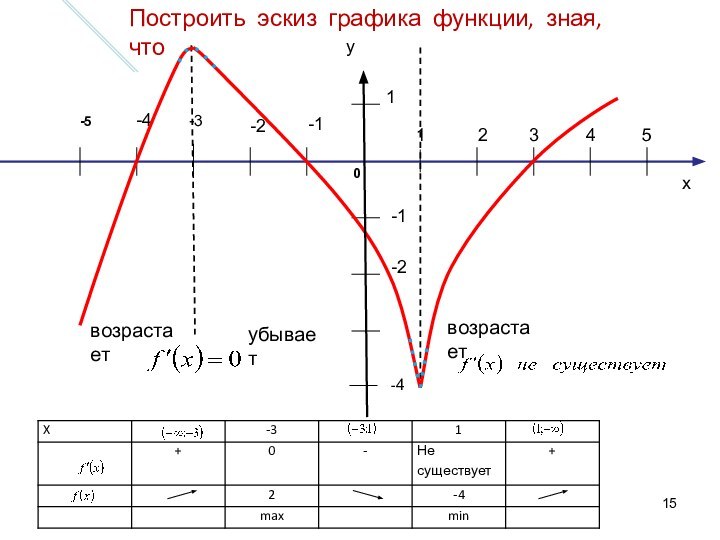
Внутренние точки области определения функции, в которых производная равна нулю или производная не существует, называются критическими.
Касательная в таких точках графика не существует, а поэтому производная в этих точках не существует.
плавные линии
угловатые линии
точка
точка
точка
точка
точка
точка
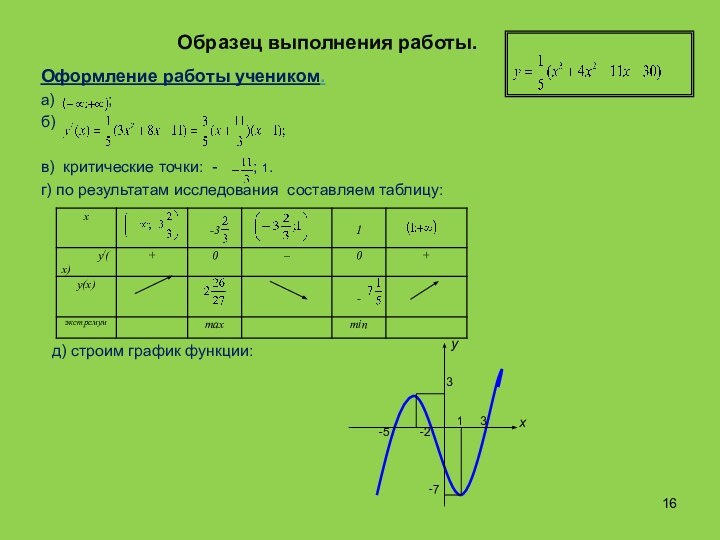
д) строим график функции:
1 3
х
у
-5 -2
3
-7