- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Применение производной к исследованию функций
Содержание
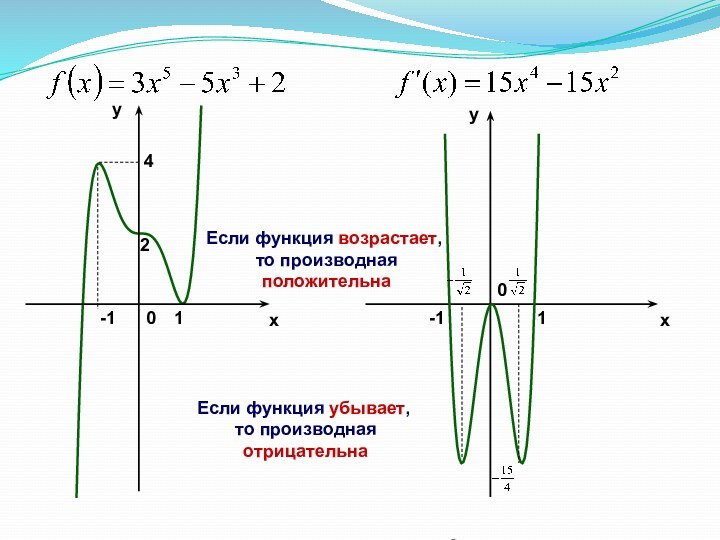
- 2. xyyx2-1140-110Если функция возрастает, то производная положительнаЕсли функция убывает, то производная отрицательна
- 4. Находим производную функцииНаходим критические точки функцииЕсли критических
- 5. х = 1 ;
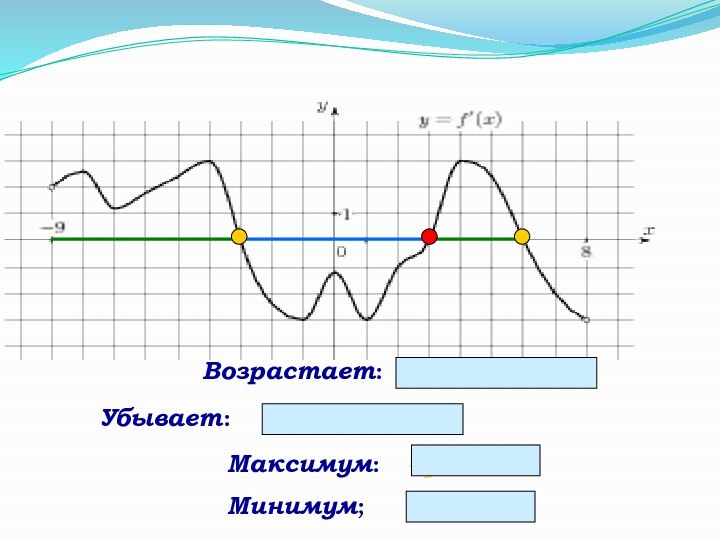
- 6. -9 -8 -7 -6 -5 -
- 7. -9 -8 -7 -6 -5 -
- 8. Непрерывная функция у = f(x) задана на
- 9. На рисунке изображен график производной функции у
- 10. y = f /(x) 1 2
- 11. y = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума
- 12. На рисунке изображен график функции f(x),
- 13. На рисунке изображен график y=f'(x) — производной
- 14. На рисунке изображен график y=f'(x) — производной
- 15. На рисунке изображен график y=f'(x) — производной
- 16. Скачать презентацию
- 17. Похожие презентации
xyyx2-1140-110Если функция возрастает, то производная положительнаЕсли функция убывает, то производная отрицательна
![Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен](/img/tmb/13/1292365/bfcafea107c3849cb58ef122426ca8a2-720x.jpg "Применение производной к исследованию функций")
Слайд 2
x
y
y
x
2
-1
1
4
0
-1
1
0
Если функция возрастает,
то производная
положительна
Если функция убывает,
то производная
Слайд 4
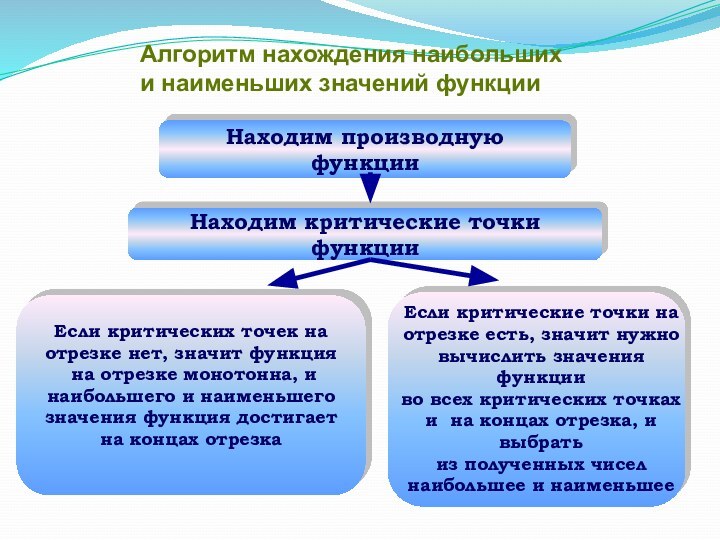
Находим производную функции
Находим критические точки функции
Если критических точек
на
отрезке нет, значит функция
на отрезке монотонна, и
наибольшего
и наименьшегозначения функция достигает
на концах отрезка
Если критические точки на отрезке есть, значит нужно вычислить значения функции
во всех критических точках и на концах отрезка, и выбрать
из полученных чисел
наибольшее и наименьшее
Алгоритм нахождения наибольших
и наименьших значений функции
Слайд 5
х = 1 ; х
= 5/3
f(-1)=18
f(3) = 2
f(1) = 6
f(5/3) = 55/9
max f(x)=f(-1)=18
[-1;3]
min f(x)=f(3)=2
[-1;3]
ответ
Решение:
Слайд 6 -9 -8 -7 -6 -5 - 4
-3 -2 -1
1 2 3 4
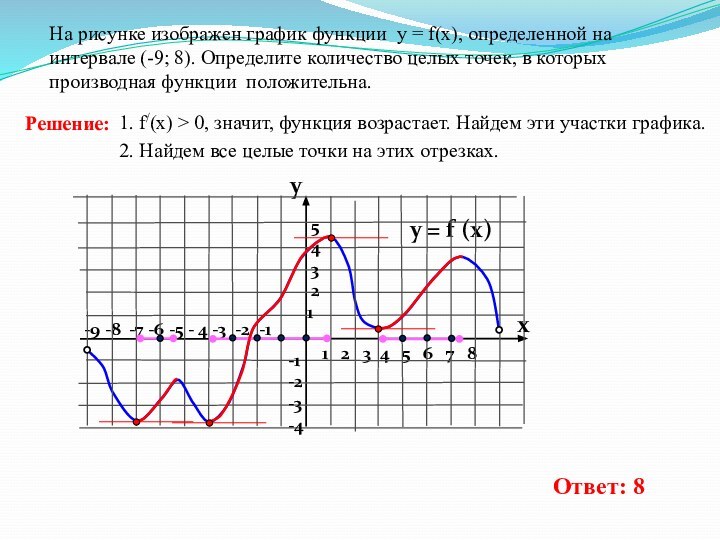
5 6 7 8На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 8
Решение:
Слайд 7 -9 -8 -7 -6 -5 - 4
-3 -2 -1
1 2 3 4
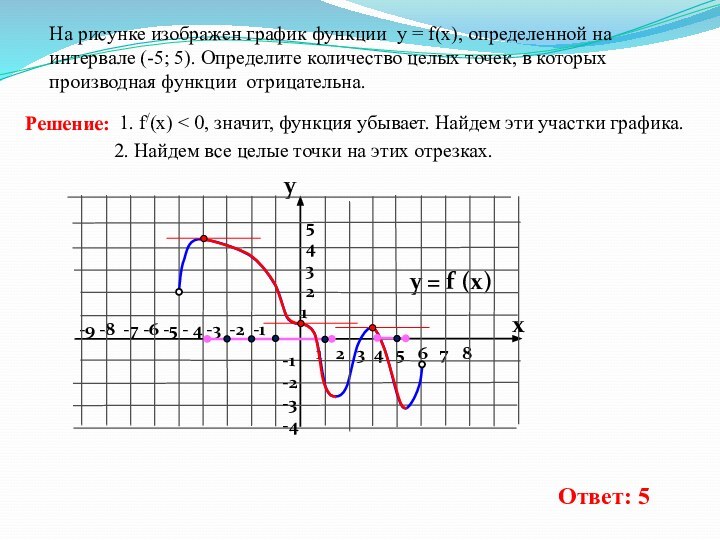
5 6 7 8На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции отрицательна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 5
Решение:
Слайд 8 Непрерывная функция у = f(x) задана на отрезке
[a;b]
На рисунке изображен ее график. В ответе укажите
количество точек графика этой функции, в которых касательная параллельна оси Ох. y = f(x)
y
x
Ответ: 5
a
b
Слайд 9 На рисунке изображен график производной функции у =f
(x), заданной на промежутке (- 8; 8).
y =
f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Найдем точки, в которых f /(x)=0 (это нули функции).
+
–
–
+
+
Слайд 10
y = f /(x)
1 2 3
4 5 6 7
-7 -6 -5
-4 -3 -2 -14
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
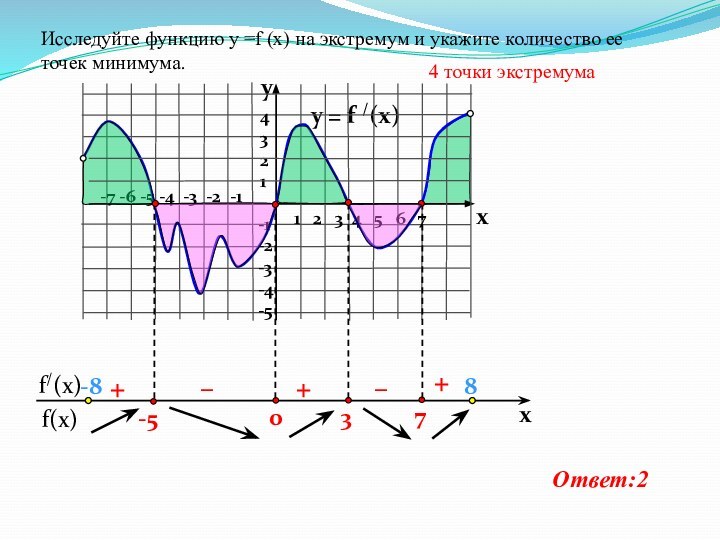
Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
4 точки экстремума
Ответ:2
-8
8
Слайд 11
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
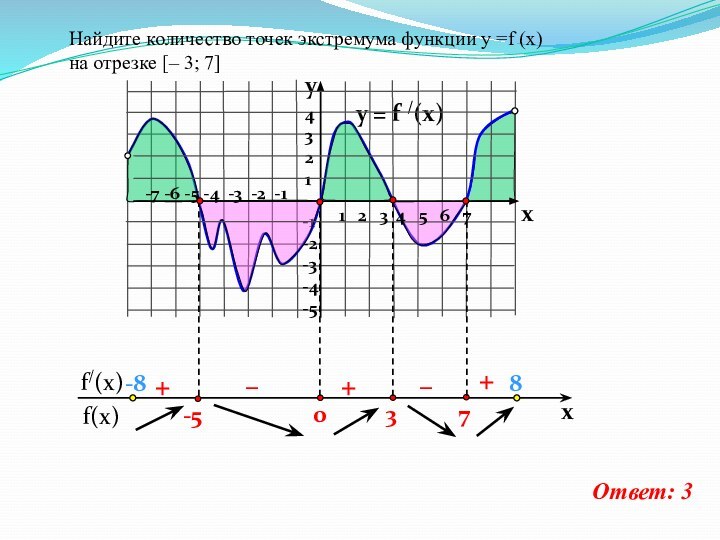
Найдите количество точек экстремума функции
у =f (x)
на отрезке [– 3; 7]
Ответ: 3
1
2 3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
-8
8
Слайд 12
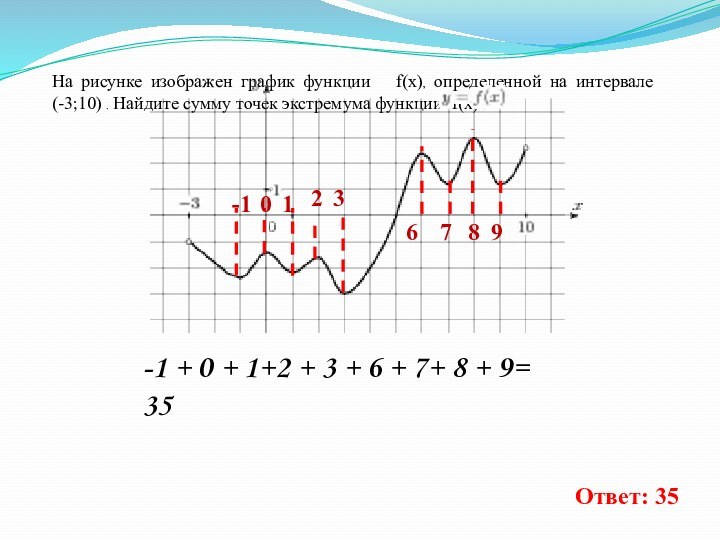
На рисунке изображен график функции f(x), определенной
на интервале (-3;10) . Найдите сумму точек экстремума функции
f(x) .-1
0
1
3
6
7
8
9
-1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35
Ответ: 35
2
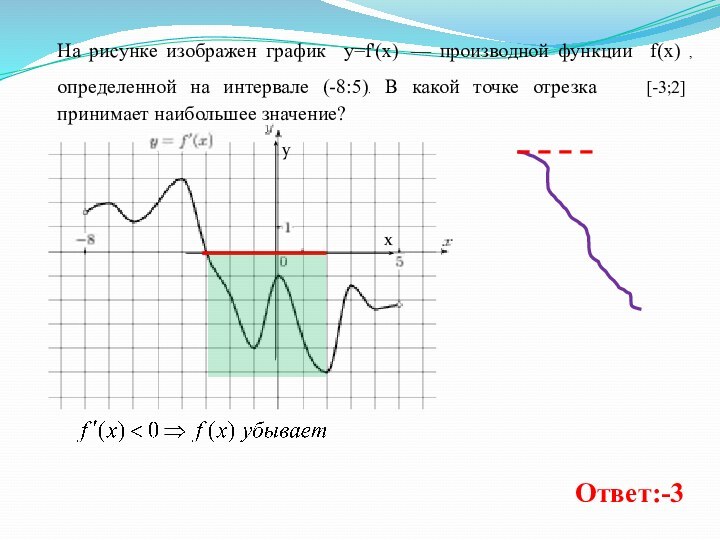
Слайд 13 На рисунке изображен график y=f'(x) — производной функции
f(x) , определенной на интервале (-8:5). В какой точке
отрезка [-3;2] принимает наибольшее значение?Ответ:-3
Слайд 14
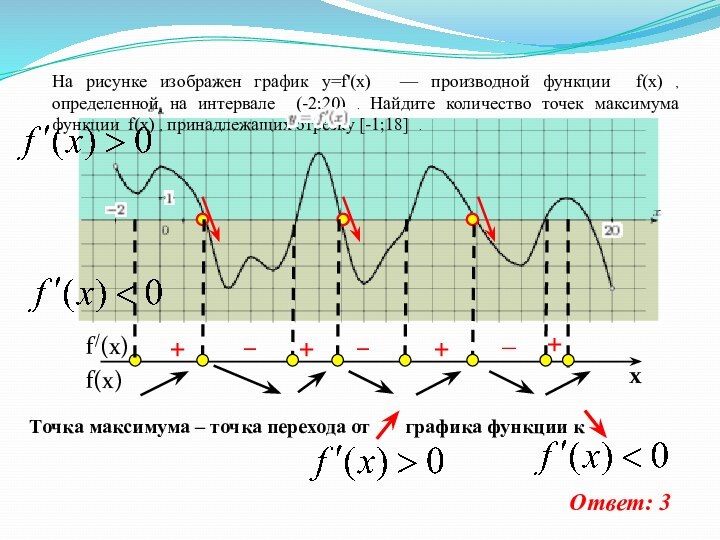
На рисунке изображен график y=f'(x) — производной функции
f(x) , определенной на интервале (-2;20) . Найдите количество
точек максимума функции f(x) , принадлежащих отрезку [-1;18] .Ответ: 3
_
–
–
+
+
+
+
Слайд 15
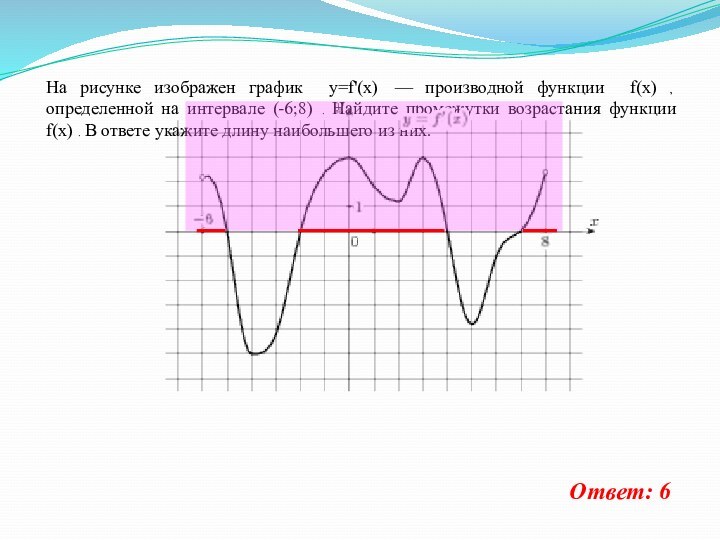
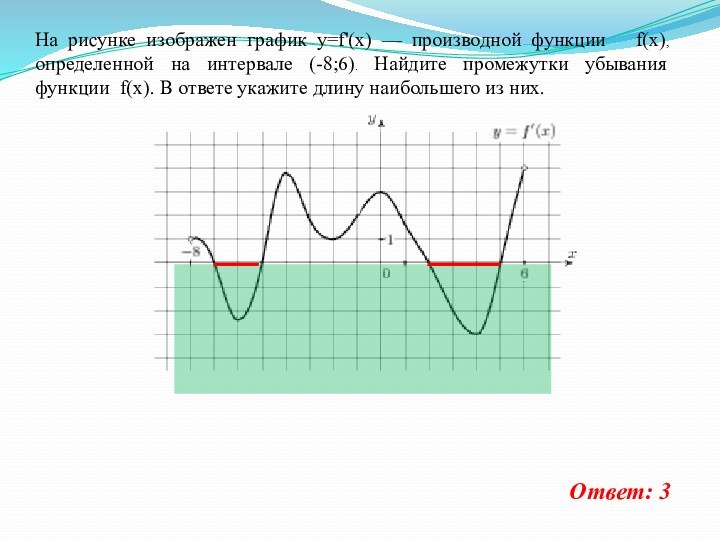
На рисунке изображен график y=f'(x) — производной функции
f(x) , определенной на интервале (-6;8) . Найдите промежутки
возрастания функции f(x) . В ответе укажите длину наибольшего из них.Ответ: 6
