- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Признак перпендикулярности плоскостей
Содержание
- 2. ОпределениеДве пересекающиеся плоскости называются перпендикулярными, если третья
- 3. ТеоремаПризнак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. св
- 4. Устная задачаАВСDМАВСD – прямоугольникМВ перпендикулярна плоскости прямоугольникаДоказать перпендикулярность плоскостей (АВМ) и (МСВ)
- 5. Задача с
- 6. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
- 8. ОПРЕДЕЛЕНИЕ. Геометрическое тело или многогранник, состоящий из
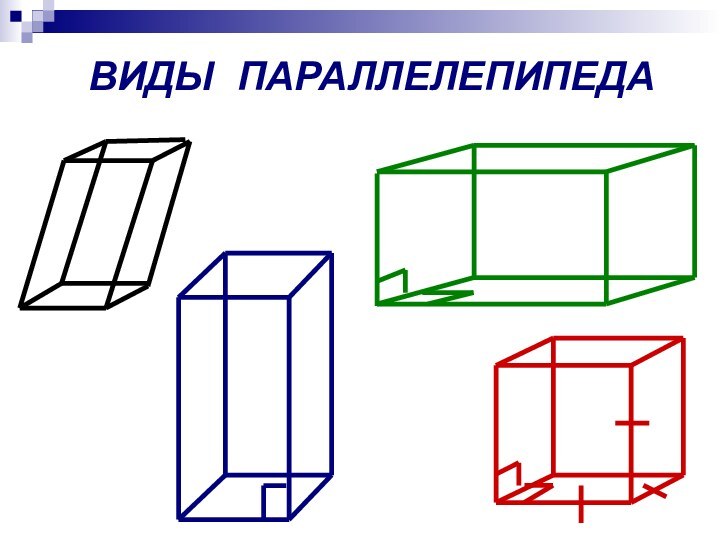
- 9. ВИДЫ ПАРАЛЛЕЛЕПИПЕДА
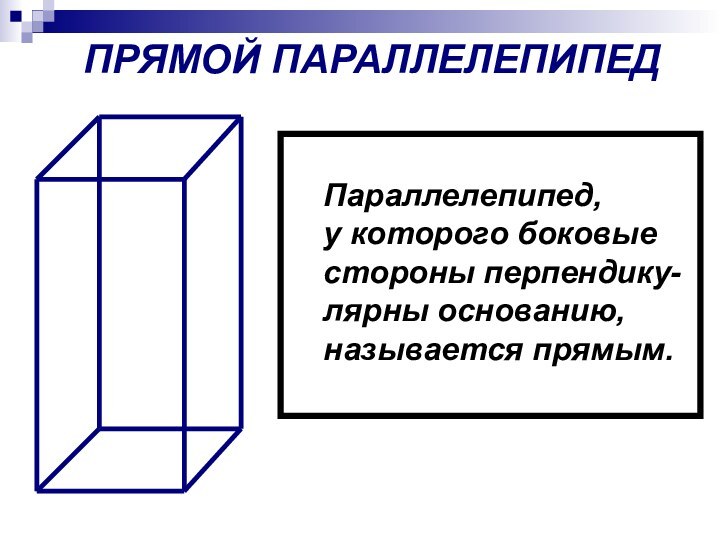
- 10. ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПараллелепипед, у которого боковые стороны перпендику-лярны основанию, называется прямым.
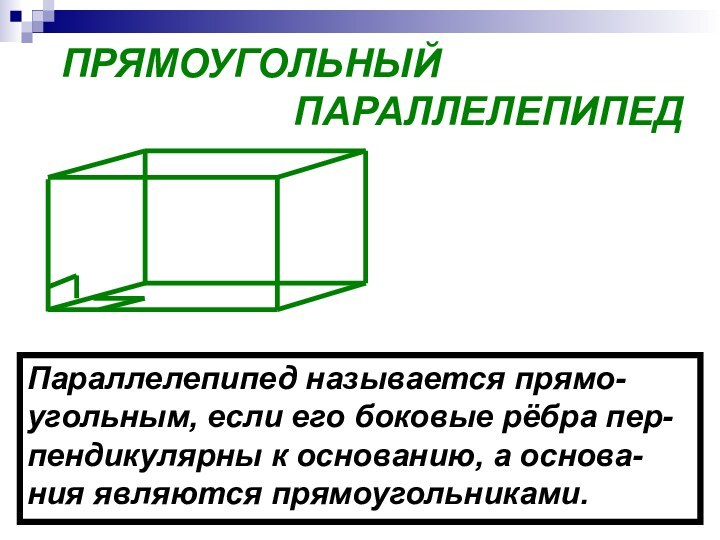
- 11. ПРЯМОУГОЛЬНЫЙ
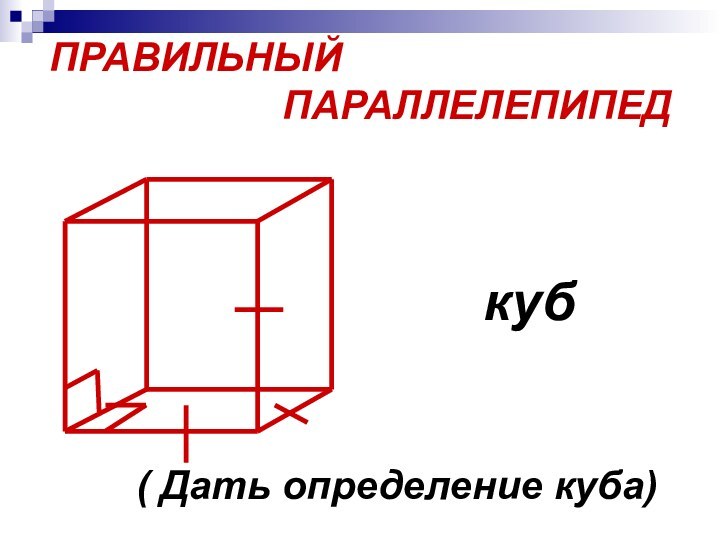
- 12. ПРАВИЛЬНЫЙ
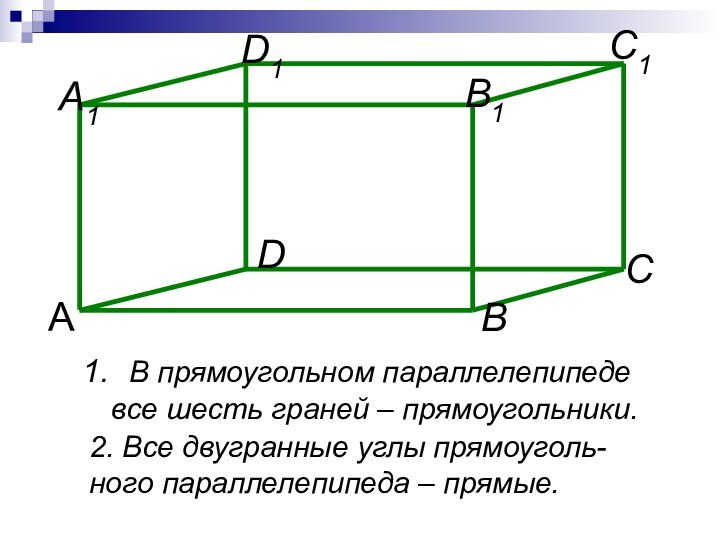
- 13. В прямоугольном параллелепипеде все шесть
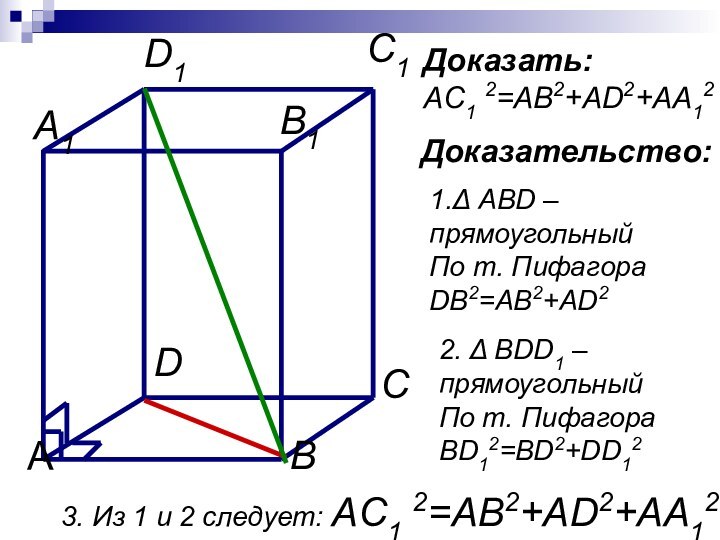
- 14. Доказать:AC1 2=AB2+AD2+AA12Доказательство:1.Δ ABD –прямоугольныйПо т. ПифагораDB2=AB2+AD22. Δ
- 16. Площадь поверхности прямоугольного параллелепипеда-это сумма площадей его граней.cabРазвертка прямоугольного параллелепипеда2ab + 2ac+ 2bc
- 21. Скачать презентацию
- 22. Похожие презентации
ОпределениеДве пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
Слайд 2
Определение
Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость,
Слайд 3
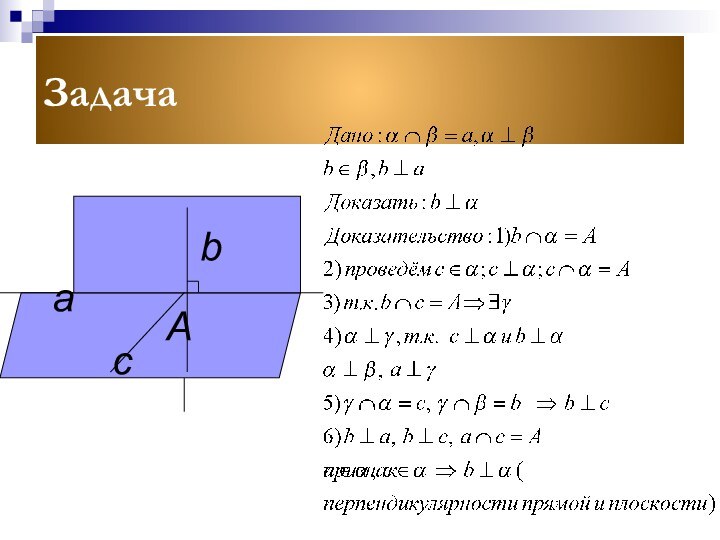
Теорема
Признак перпендикулярности плоскостей.
Если плоскость проходит через прямую,
перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
с
в
Слайд 4
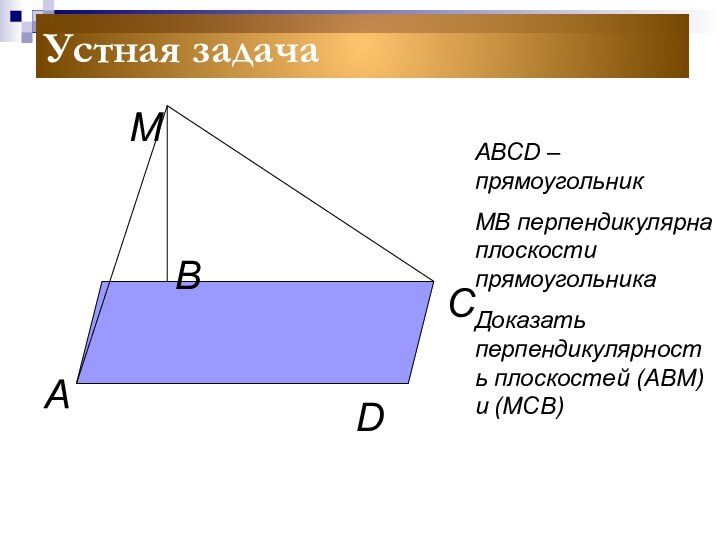
Устная задача
А
В
С
D
М
АВСD – прямоугольник
МВ перпендикулярна плоскости прямоугольника
Доказать перпендикулярность
плоскостей (АВМ) и (МСВ)
Слайд 8
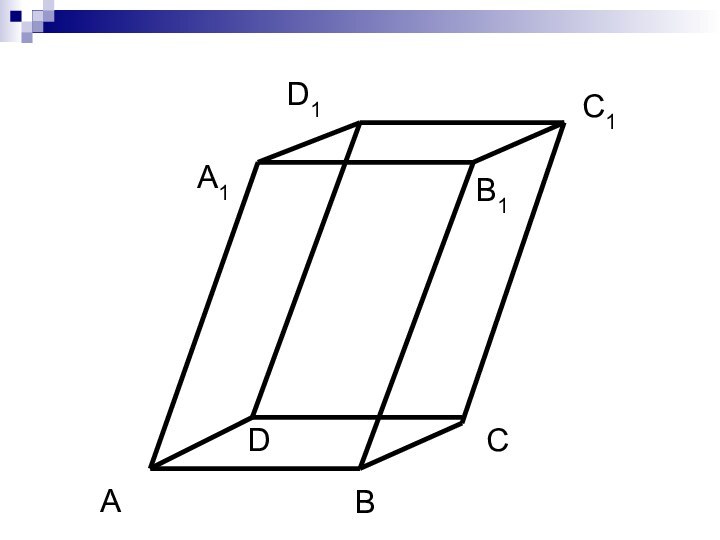
ОПРЕДЕЛЕНИЕ.
Геометрическое тело или многогранник, состоящий из трёх
пар равных паралле- лограммов лежащих в парал-
лельных плоскостях, называ-
ется
параллелепипедом(Назвать вершины, рёбра, грани и их количество.)
Слайд 10
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Параллелепипед,
у которого боковые
стороны перпендику-
лярны основанию,
называется прямым.
Слайд 11
ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямо-
угольным, если его
боковые рёбра пер- пендикулярны к основанию, а основа- ния являются прямоугольниками.
Слайд 13
В прямоугольном параллелепипеде
все шесть
граней – прямоугольники.
2. Все двугранные углы прямоуголь- ного параллелепипеда
– прямые.
Слайд 14
Доказать:
AC1 2=AB2+AD2+AA12
Доказательство:
1.Δ ABD –прямоугольный
По т. Пифагора
DB2=AB2+AD2
2. Δ BDD1
–
прямоугольный
По т. Пифагора
BD12=BD2+DD12
3. Из 1 и
2 следует: AC1 2=AB2+AD2+AA12Слайд 16 Площадь поверхности прямоугольного параллелепипеда-это сумма площадей
