Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Производная функции

Содержание

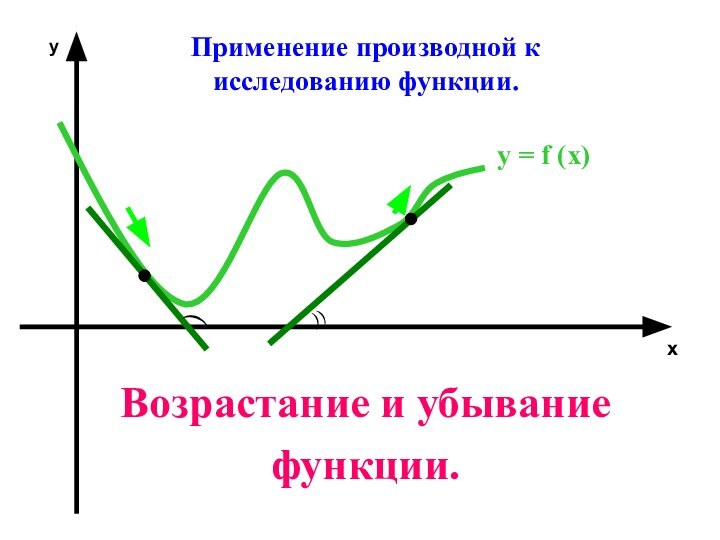
2. Применение производной к исследованию функции.Возрастание и убываниефункции.)хуу = f (х)))
3. Повторение: ~ определение возрастающей и
4. 1. Монотонность функции.1.1 Возрастающая функция.хх1х2у = f
5. 1. Монотонность функции.1.2 Убывающая функция.хх1х2у = f
6. 1. Монотонность функции. 1.3 Возрастающие и
7. 2. Геометрический смысл производной.у = f (х)Ах0f
8. Вы умеете с помощью графика функции определять
9. 3. Установление связи между характером монотонности функции
10. 3. Установление связи между характером монотонности функции
11. 3. Установление связи между характером монотонности функции
12. 3. Установление связи между характером монотонности функции
13. 3. Установление связи между характером монотонности функции
14. 4. Решение заданий. f(х) = х 4
15. 4. Решение заданий. f(х) =1/ (х+2) 1.
16. 4. Решение заданий. f(х) = х +4/х
17. возрастающая функция
18. Скачать презентацию
19. Похожие презентации

Применение производной к исследованию функции.Возрастание и убываниефункции.)хуу = f (х)))

Мы продолжаем изучать тему «Производная функции»Мы познакомимся с применением производной для исследования

Повторение: ~ определение возрастающей и убывающей функций ~ геометрический смысл

1. Монотонность функции.1.1 Возрастающая функция.хх1х2у = f (х)у f (х1)f (х2)Функция f(х)

1. Монотонность функции.1.2 Убывающая функция.хх1х2у = f (х)у f (х1)f (х2)Функция f(х)

1. Монотонность функции. 1.3 Возрастающие и убывающие функции

2. Геометрический смысл производной.у = f (х)Ах0f (х0))у = к х +

Вы умеете с помощью графика функции определять промежутки монотонности функцииМожно ли без

3. Установление связи между характером монотонности функции и знаком ее производной.хуу =

3. Установление связи между характером монотонности функции и знаком ее производной.3.3у =

3. Установление связи между характером монотонности функции и знаком ее производной.3.4у =

3. Установление связи между характером монотонности функции и знаком ее производной.3.5

4. Решение заданий. f(х) = х 4 - 2 х 2 1.

4. Решение заданий. f(х) =1/ (х+2) 1. Д(f) : 2. f (х)

4. Решение заданий. f(х) = х +4/х 1. Д(f) : 2. f

возрастающая функция убывающей функций геометрический смысл

Слайды презентации

Слайд 2 Применение производной к исследованию функции.
Возрастание и убывание
функции.
)
х
у

у = f

(х)

)
)

Слайд 3
Повторение:

~ определение возрастающей и убывающей

функций
~ геометрический смысл производной

Изучение нового материала:

~ установление зависимости между характером
монотонности функции и знаком её производной

~ алгоритм нахождения промежутков
монотонности функции

~ решение заданий

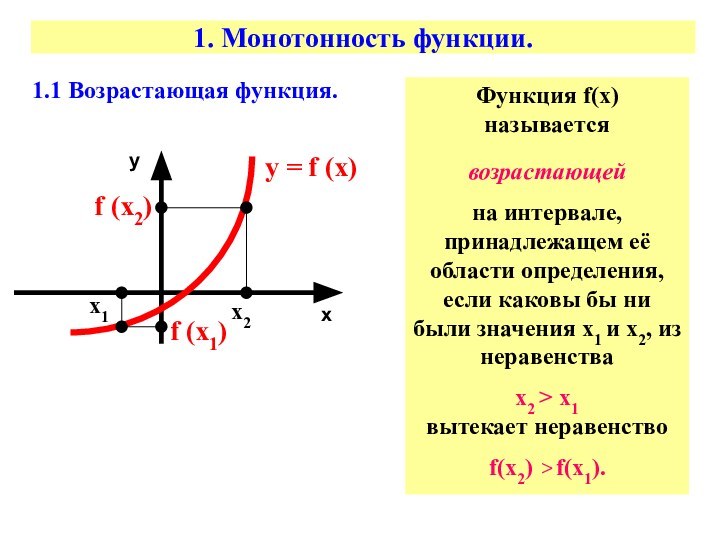
Слайд 4 1. Монотонность функции.
1.1 Возрастающая функция.

х
х1
х2

у = f (х)
у

1. Монотонность функции.1.1 Возрастающая функция.хх1х2у = f (х)у f (х1)f (х2)Функция

f (х1)
f (х2)
Функция f(х) называется
возрастающей
на интервале, принадлежащем её

области определения, если каковы бы ни были значения х1 и х2, из неравенства
х2 > х1 вытекает неравенство
f(х2) > f(х1).

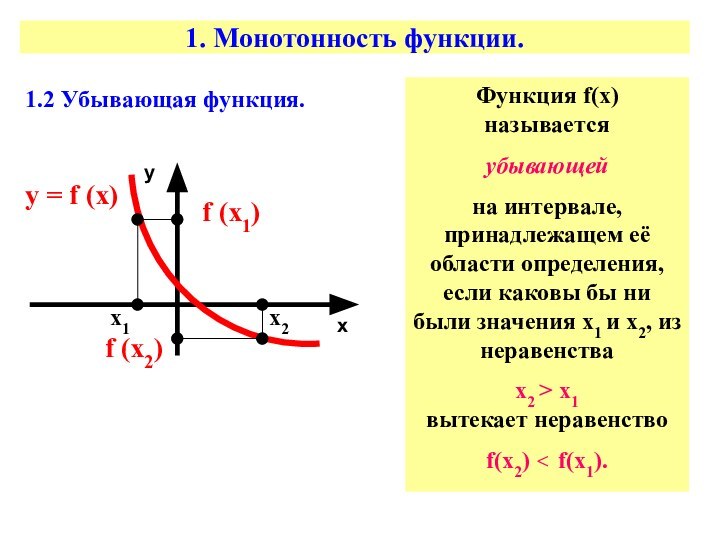
Слайд 5 1. Монотонность функции.
1.2 Убывающая функция.

х
х1
х2

у = f (х)
у

1. Монотонность функции.1.2 Убывающая функция.хх1х2у = f (х)у f (х1)f (х2)Функция

f (х1)
f (х2)

Функция f(х) называется
убывающей
на интервале, принадлежащем её области

определения, если каковы бы ни были значения х1 и х2, из неравенства
х2 > х1 вытекает неравенство
f(х2) < f(х1).

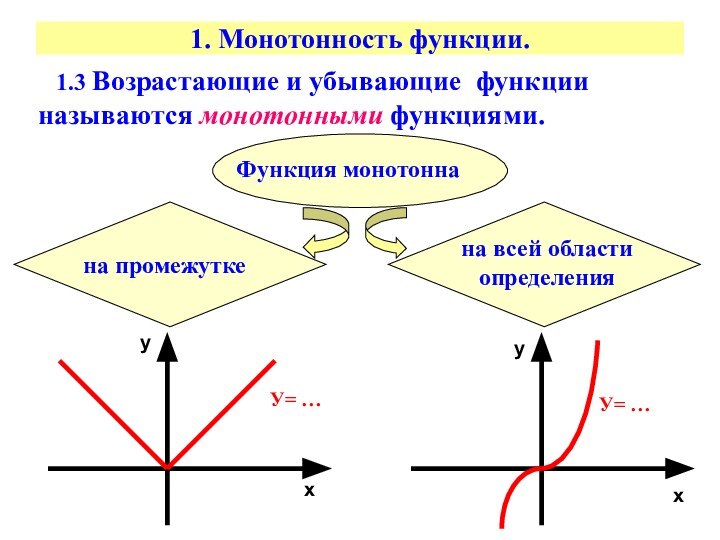
Слайд 6 1. Монотонность функции.
1.3 Возрастающие и убывающие

1. Монотонность функции. 1.3 Возрастающие и убывающие функции называются монотонными

функции называются монотонными функциями.

Функция монотонна

на всей

области определения

на промежутке

У= …

Слайд 7 2. Геометрический смысл производной.

у = f (х)
А
х0
f (х0)
)
у

= к х + в
х
у
у = f (х0) (

х-х0) + f(х0)

f (х0) = к = t g

у = f (х)

Слайд 8

Вы умеете
с помощью графика функции
определять промежутки

Вы умеете с помощью графика функции определять промежутки монотонности функцииМожно ли

монотонности функции

Можно ли без построения
графика функции
определять характер
монотонности функции?

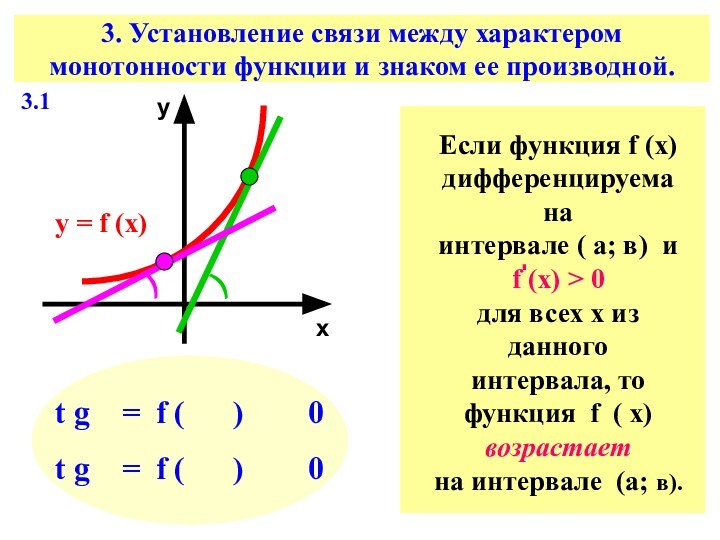
Слайд 9 3. Установление связи между характером монотонности функции и

знаком ее производной.
х
у

у = f (х)

)
)

t g =

f ( ) 0

t g = f ( ) 0

Если функция f (х)
дифференцируема на
интервале ( а; в) и
f (х) > 0
для всех х из данного
интервала, то
функция f ( х)
возрастает
на интервале (а; в).

3.1

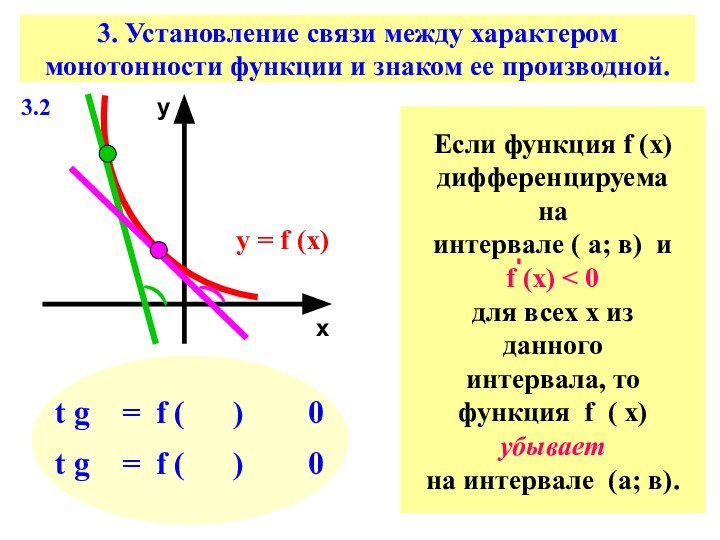
Слайд 10 3. Установление связи между характером монотонности функции и

знаком ее производной.
х
у

у = f (х)
)
)

t g =

f ( ) 0

t g = f ( ) 0

Если функция f (х)
дифференцируема на
интервале ( а; в) и
f (х) < 0
для всех х из данного
интервала, то
функция f ( х)
убывает
на интервале (а; в).

3.2

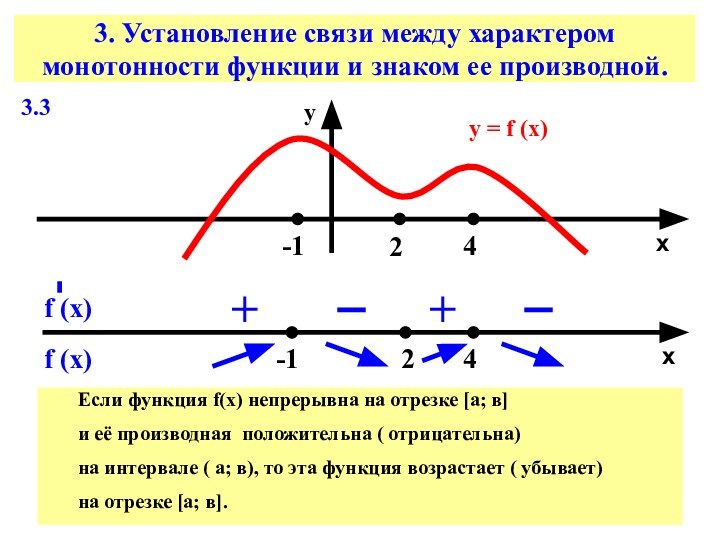
Слайд 11 3. Установление связи между характером монотонности функции и

знаком ее производной.
3.3

у = f (х)
х
х
у

-1
-1

2
2
4
4
f (х)
f (х)
+
+
Если функция

f(х) непрерывна на отрезке [а; в]
и её производная положительна ( отрицательна)
на интервале ( а; в), то эта функция возрастает ( убывает)
на отрезке [а; в].

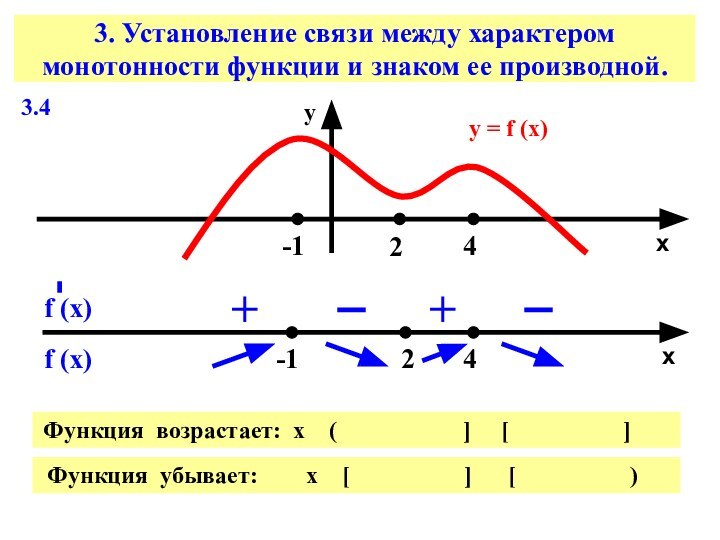
Слайд 12 3. Установление связи между характером монотонности функции и

знаком ее производной.
3.4

у = f (х)
х
х
у

-1
-1

2
2
4
4
f (х)
f (х)
+
+

Функция

возрастает: х ( ] [ ]

Функция убывает: х [ ] [ )

Слайд 13 3. Установление связи между характером монотонности функции и

знаком ее производной.
3.5

Алгоритм нахождения

промежутков
монотонности функции.
1. Найти область определения функции.
2. Найти производную функции.
3. Найти значения аргумента,
при которых значение производной
больше нуля, меньше нуля.
4. Сделать вывод.