Презентация на тему Объём пирамиды

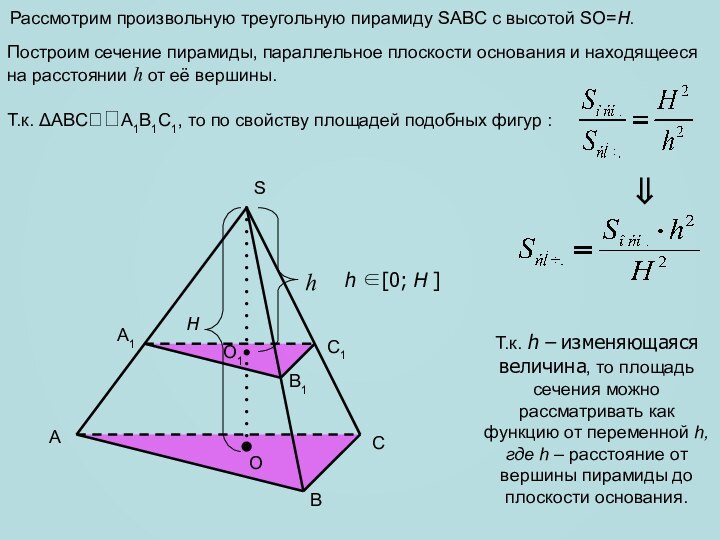
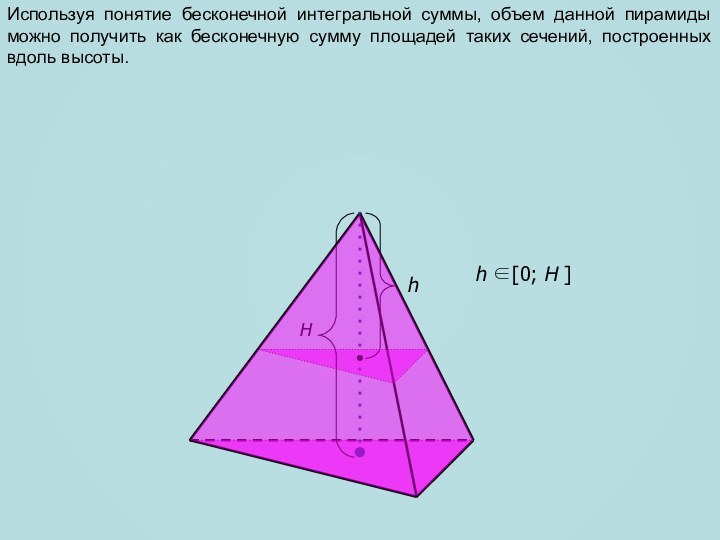
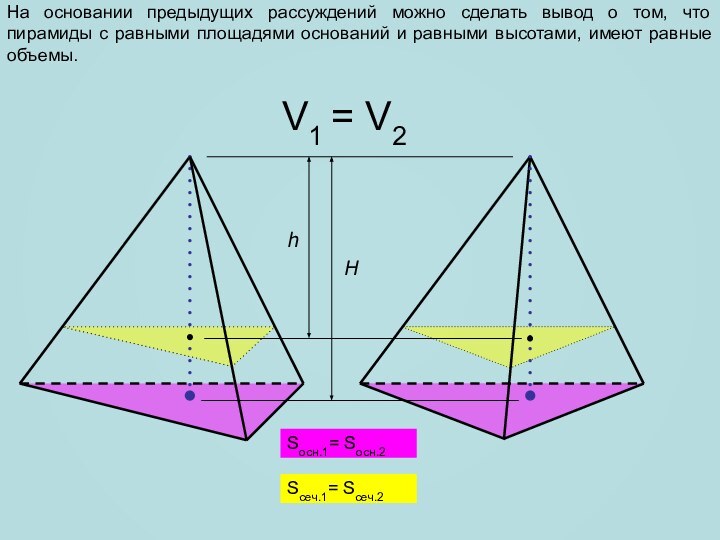
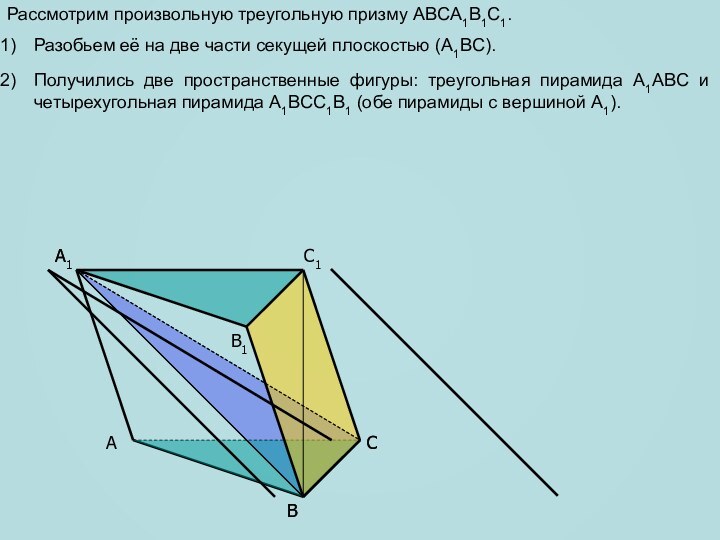
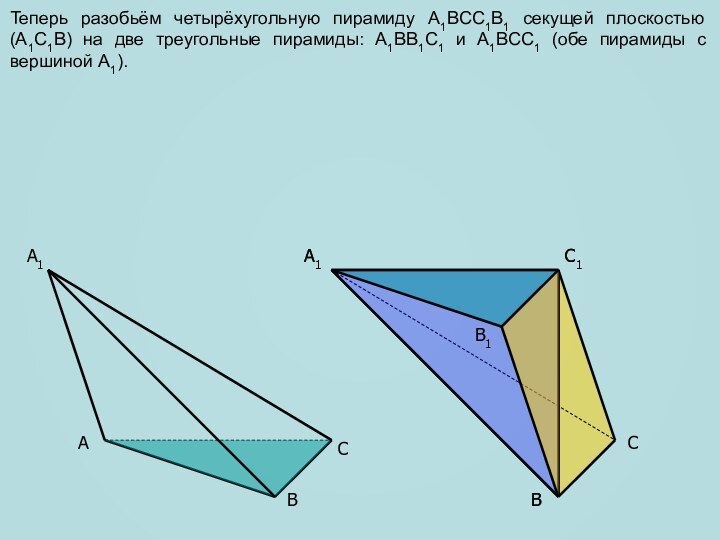
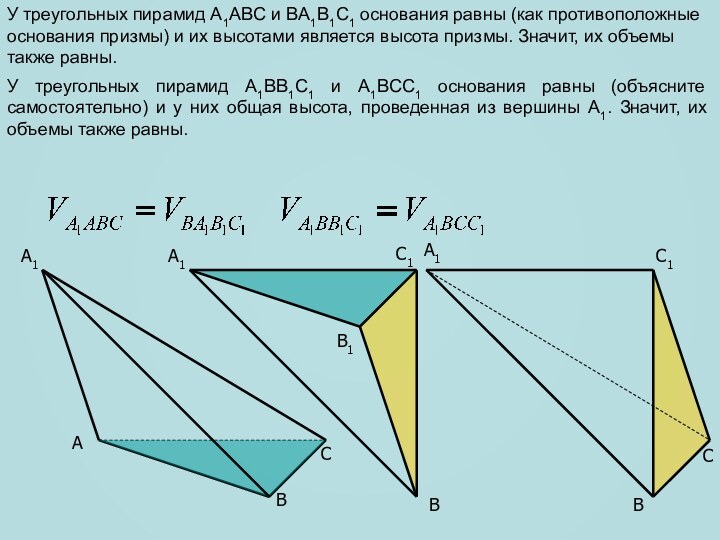
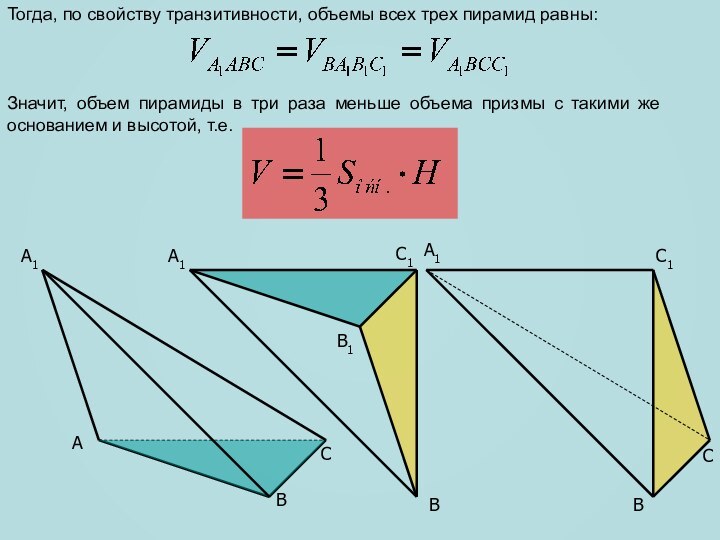
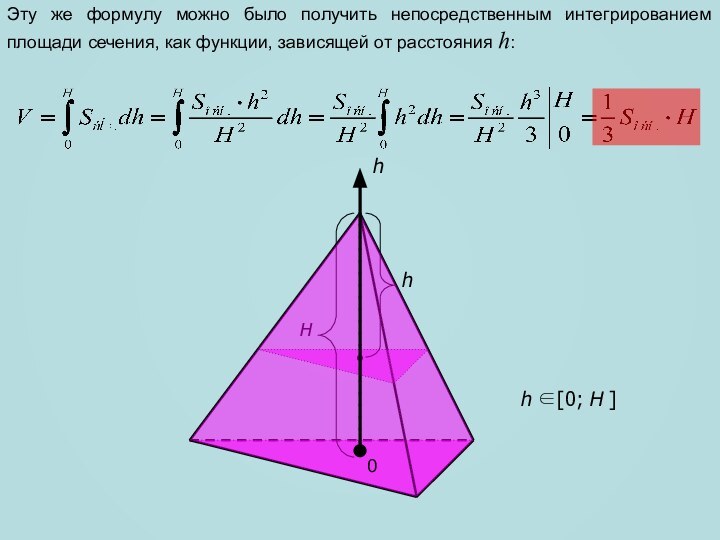
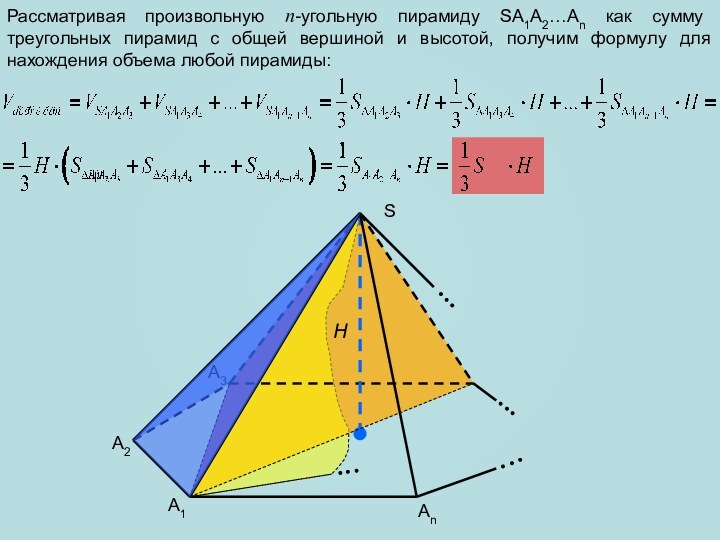
сечение пирамиды, параллельное плоскости основания и находящееся на расстоянии

Т.к. ABCA1B1C1, то по свойству площадей подобных фигур :

A1

C1

B1

h [0; H ]



Т.к. h – изменяющаяся величина, то площадь сечения можно рассматривать как функцию от переменной h, где h – расстояние от вершины пирамиды до плоскости основания.

можно получить как бесконечную сумму площадей таких сечений, построенных

h [0; H ]

том, что пирамиды с равными площадями оснований и равными

H

Sосн.1= Sосн.2

V1 = V2

h

Sсеч.1= Sсеч.2

части секущей плоскостью (A1BC).
Получились две пространственные фигуры: треугольная пирамида

на две треугольные пирамиды: A1BB1C1 и A1BCC1 (обе пирамиды

A1

C1

B

(как противоположные основания призмы) и их высотами является высота

У треугольных пирамид A1BB1C1 и A1BCC1 основания равны (объясните самостоятельно) и у них общая высота, проведенная из вершины A1. Значит, их объемы также равны.

равны:
Значит, объем пирамиды в три раза меньше объема призмы

площади сечения, как функции, зависящей от расстояния h:
h [0;

0

пирамид с общей вершиной и высотой, получим формулу для

S

A3

An

A2

A1

H