Слайд 2
Цель, задачи
Цель– представить наблюдаемые данные в компактной и
простой форме, позволяющей выявить имеющиеся закономерности и связи
Разведочный анализ
данных (РАД) включает:
преобразование данных и способы наглядного их представления
выявление аномальных значений
грубая оценка типа распределения
сглаживание
Слайд 3
Вопросы анализа данных
Какой обработке подвергнуть наблюдения?
Какую
модель выбрать?
Какие заключения можно сделать?
Слайд 4
Пример РАД
Разведочный анализ (Exploratory data analysis) – средство
получения более полной информации об изучаемом явлении
Наблюдения n пар
(x1,Y1), …, (xn,Yn) опишем уравнением
(1)
Минимальный предварительный анализ - график рассеяния точек (xj,Yj).
Слайд 5
Предварительная обработка данных. Оценка среднего
Оценка -
истинного среднего m независимой случайной величины x по выборке
объема n
Доверительный интервал:
t-распределение Стьюдента:
95%-е доверительные интервалы
Для нормального распределения t = 1,96,
Для t-распределения при числе степеней свободы v (v = n – 1), равных 1; 3 и 12, величина t, соответственно, равна 12,7; 4,3 и 2,18.
Слайд 6
Причины отличия реального распределения от нормального
Большинство измерений проводится
в конкретных единицах
Резкая асимметрия некоторых распределений (например,χ2, F) при
малых выборках, обрывистые края у равномерного распределения
Поведение на «хвостах» распределения, которое существенно отличается от значений основного количества наблюдений
Слайд 7
Робастные оценки
Робастные оценки - robust – крепкий, здоровый,
Пример робастной оценки среднего, терпимой к отклонению хвостов распределения
от нормального - медиана распределения
Слайд 8
Мера разброса
среднеквадратическое отклонение σ
дисперсия σ2
размах R
Оценки этих
величин обозначают, соответственно, S, S2, R
Оценка разброса по S
– в линейных преобразованиях типа Y = β + αX
Слайд 9
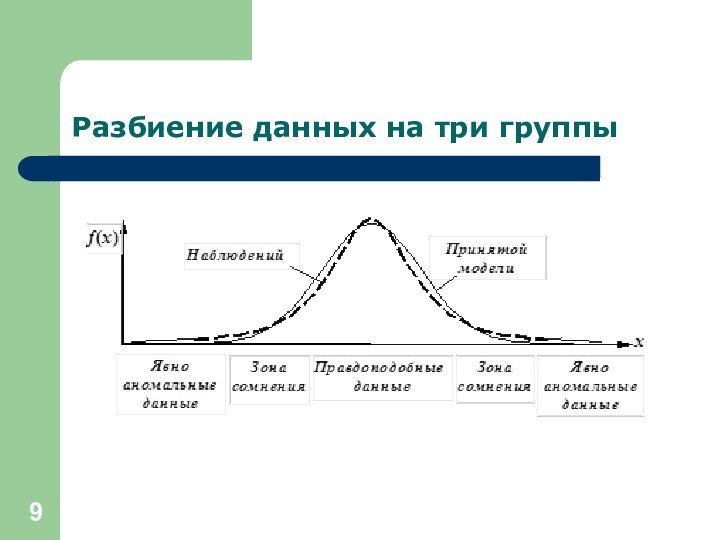
Разбиение данных на три группы
Слайд 10
Качество результатов
Простая перепроверка. Проверка полученной модели на данных,
отличных от тех, по которым определены параметры модели
Двойная перепроверка.
Проверка на данных отличных, как от тех, по которым строилась модель, так и от тех, которые использованы для вычисления параметров модели
Слайд 12
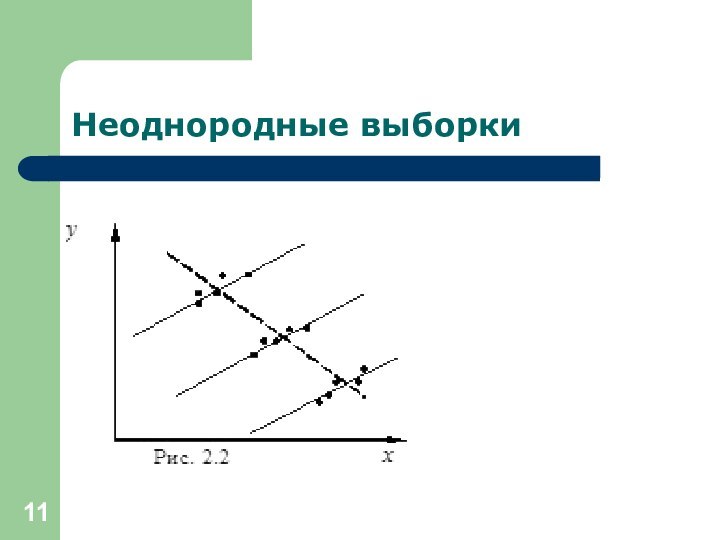
Разделение неоднородной совокупности на однородные
Пусть выборка
изучаемой совокупности x1, …, xn, содержит элементы двух независимых
случайных величин с плотностями распределений f(x,θ1) и f(x,θ2).
Обозначим через А – множество элементов выборки, принадлежащих к первой случайной величине, В – множество элементов выборки из второй совокупности.
Требуется найти оценки неизвестных параметров θ1, θ2 и множества А и В.
Для оценки этих четырех неизвестных используем метод максимума правдоподобия
Слайд 13
Обнаружение аномальных наблюдений
Причины:
грубые ошибки при регистрации
измерений,
случайные импульсные помехи,
сбои оборудования,
измерения в ошибочных
единицах
и др.
Слайд 14
Обнаружение аномальных наблюдений. Критерий проверки
Пусть
наблюдения x1, …, xn являются реализациями независимых случайных величин,
подчиняющихся одинаковому нормальному N(μ,σ2) распределению
Основная гипотеза H0: Mxi = μ, Dxi = σ2, i = 1, …, n.
Альтернативная гипотеза H1 : одна или несколько величин имеют среднее μ + d
Слайд 15
Обнаружение аномальных наблюдений. Критерий проверки
При построении критерия
возможны варианты, зависящие от степени информации о μ и
σ.
Рассмотрим случай, когда значения μ и σ неизвестны. Критериальная статистика:
Распределение величины Dn получены К. Пирсоном и Н.В. Смирновым. Критические значения Dn, вычислены Н.В. Смирновым и Ф. Граббсом
H0 - Dn < Dα - наблюдение не является аномальным
H1 - Dn > Dα - наблюдение является аномальным
Слайд 16
Общие выводы об удалении аномальных наблюдений
Для данных с
неправдоподобными наблюдениями использовать робастные процедуры оценивания
Существенно выделяющиеся данные обнаруживать,
преобразовывать и удалять, при этом интерпретировать, привлекая знания, не относящиеся к статистической природе
Процедуры удаления существенно выделяющихся и подозрительно больших наблюдений с последующим оцениванием близких к робастным оценкам
Слайд 17
Простые числовые и графические сводки данных
Процедура «стебель с
листьями» (Stem-and-Leaf)
250 688 695 795 795 895 895 895
1099 1166 1333 1499 1693 1699 1775 1895
Три вида записи «стебля с листьями» цен на 17 автомобилей «Шевроле»: а – единица = 100 $; б – единица = 10 $; в – единица = 100 $