нечеткой логики;
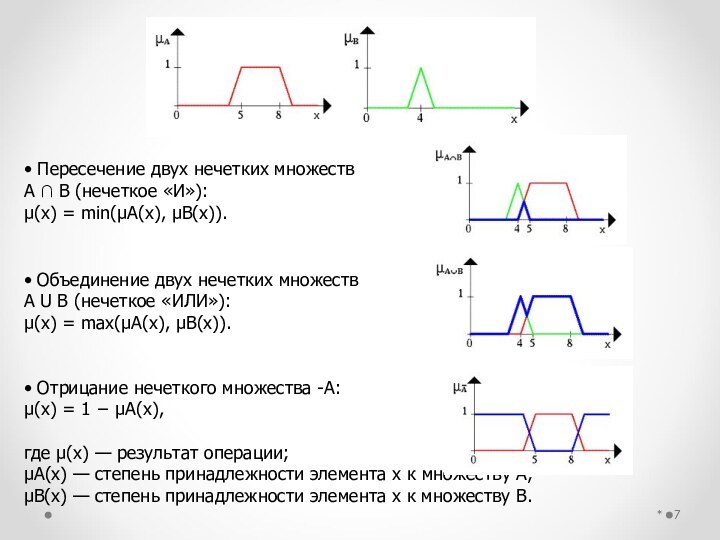
логические операции с нечеткими множествами;
графическое и математическое представление
логических операций.Определить связь четкой и нечеткой логик.
Уметь:
графически представлять логические операции с нечеткими множествами;
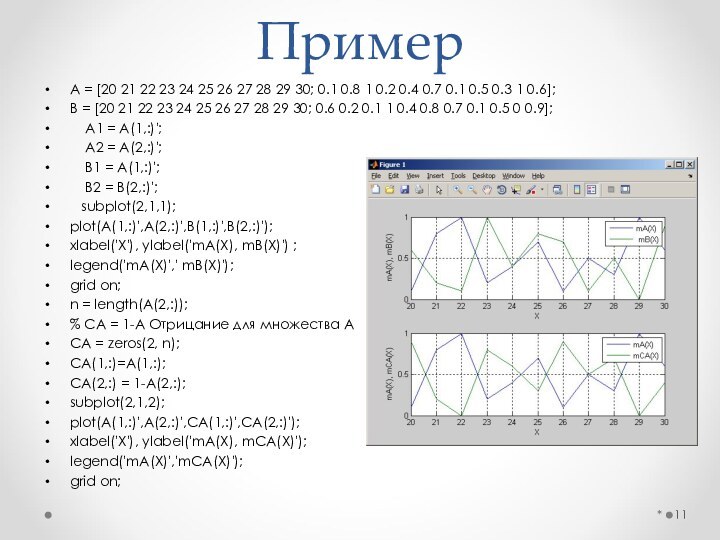
находить пересечение, объединение, разность двух нечетких множеств и представлять данные операции в виде формул;
применять унарные операции умножения числа на нечеткое множество и возведение нечеткого множества в степень.
*