Слайд 2
Правила
Игра состоит из 10 туров. В каждом туре
3 варианта заданий (на выбор учащегося)
Тему задания выбирают по
очереди (решаем 10 заданий)
Задание решают все учащиеся
За правильный ответ – 1 бал.
Каждый играет за себя
Набрать надо не менее 8 баллов.
Слайд 3
Содержание
1 тур
2 тур
3 тур
4 тур
5 тур
6 тур
7
тур
8 тур
9 тур
10 тур
ИТОГ
Слайд 4
1 тур
Геометрия
Функции
Алгебраические выражения
Слайд 5
2 тур
Упростить выражение
Уравнения
Геометрическая задача
Слайд 6
3 тур
Текстовая задача
Найти значение выражения
Реальная математика
Слайд 7
4 тур
Теория вероятностей
Неравенства
Свойства чисел
Слайд 8
5 тур
Найти верные
утверждения
Задача
Свойства степени
Слайд 9
6 тур
Формулы
Текстовая задача
Функции
Слайд 10
7 тур
Уравнения
Геометрическая задача
Свойства числовых неравенств
Слайд 11
8 тур
Последовательности
Геометрия
Алгебраические выражения
Слайд 12
9 тур
Уравнения
Статистика и теория вероятностей
Реальная математика
Слайд 14
Задание 1 тура (геометрия)
В равнобедренном треугольнике АВС с
основанием АС внешний угол при вершине С равен 102°.
Найдите величину угла АВС. Ответ дайте в градусах.
С
А
В
102°
Ответ: 24°
Слайд 15
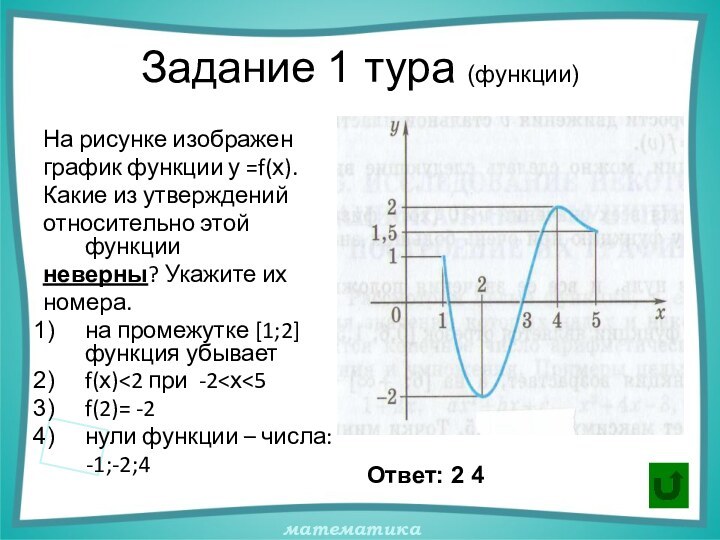
Задание 1 тура (функции)
На рисунке изображен
график функции у
=f(х).
Какие из утверждений
относительно этой функции
неверны? Укажите их
номера.
на промежутке [1;2]
функция убывает
f(х)<2 при -2<х<5
f(2)= -2
нули функции – числа:
-1;-2;4
Ответ: 2 4
Слайд 16
Задание 1 тура (алгебраические выражения)
Запишите в ответе номера
верных равенств
1) а²
- 10а + 25 = (а - 5)²
2) 25 - а² = (5 + а)(а - 5)
3) (в - 1)(а - 5) = - (1 - в)(а - 5)
4) (а + 1)(2а - 5) = 2а² + 2а – 5
Ответ:13
Слайд 17
Задание 2 тура (упростить выражение)
Упростив выражение
Найдите его значение
при
а = √2, в = √50
Ответ: -1,75
Слайд 18
Задание 2 тура (уравнения)
Какое из уравнений имеет два
различных корня?
1) х² - 2х + 5 = 0
2) 9х² - 6х + 1 = 0
3) 2х² - 7х + 2 = 0
4) 3х² - 2х + 2 = 0
Ответ: 2
Слайд 19
Задание 2 тура (геометрическая задача)
Найдите
меньший угол
равнобедренной
трапеции, если
два его
угла
относятся как 3:6. Ответ дайте в градусах.
Ответ: 60
Слайд 20
Задание 3 тура (текстовая задача)
Спортивная команда решила заказать
вышивку эмблемы своего клуба на форме членов команды. Стоимость
вышивки одной эмблемы составляет 25р.,причем, за вышивку на трикотаже стоимость увеличивается на 16%. Сколько рублей придется заплатить за заказ, если надо вышить 34 эмблемы, из которых 17 на трикотаже?
Ответ: 918 р.
Слайд 21
Задание 3 тура (найти значение выражения)
Найдите значение выражения
при
а=3; в=6
Ответ: 0,2
Слайд 22
Задание 3 тура (реальная математика)
Фирма изготавливает и продаёт
бумажные пакеты с логотипом заказчика. Стоимость заказа из 100
пакетов составляет 61р., а заказа из 300 пакетов – 123 р. На сколько процентов стоимость одного пакета при заказе 300 пакетов меньше, чем при заказе 100 пакетов? Ответ округлить до целых процентов.
т.к. 67%- стоимость 1 пакета при заказе 300 пакетов. Значит: 100-67= 33%
Ответ: на 33%
Слайд 23
Задание 4 тура (теория вероятностей)
Паша наудачу выбирает двузначное
число. Найдите вероятность того, что оно оканчивается на 7.
Решение:
Всего двузначных чисел – 90.
Двузначных чисел, оканчивающихся на 7: 17,27,37,47,57,67,77,87,97 – 9 чисел.
Вероятность того, что наугад выбранное двузначное число оканчивается на 7, равна: 9:90=0,1
Ответ: 0,1
Слайд 24
Задание 4 тура (неравенства)
Решите неравенство
2 – 3(х - 6) ≤ 27
– (1 + х)
Ответ: x ≥ -3
Слайд 25
Задание 4 тура (свойства чисел)
Укажите два соседних числа,
между которыми заключено число
1) 3 и
4 2) 4 и 5 3) 6 и 7 4) 45 и 46
Ответ: 3
Слайд 26
Задание 5 тура (найти верные утверждения)
Какие из данных
утверждений верны?
Сумма углов любого выпуклого шестиугольника равна 940°
В любой
параллелограмм можно вписать окружность
Существует только одна точка, равноудалённая от всех вершин данного треугольника
Одна из высот прямоугольного треугольника всегда делит его на два подобных треугольника.
Ответ: 3 4
Слайд 27
Задание 5 тура (задача)
Точка касания окружности, вписанной в
равнобедренный треугольник, делит одну из боковых сторон на отрезки,
равные 7см и 8см, считая от основания. Найдите периметр треугольника
Ответ: Р= 44 см
7см
8см
Слайд 28
Задание 5 тура (свойства степени)
Упростить выражение
Решение: (5ⁿ·5
- 5ⁿ: 5) \ 2· 5ⁿ =
= 5ⁿ
(5- 1\5) \ 2· 5ⁿ (сокращаем на 5ⁿ )=(24\5):2=12\5
= 2,4
Ответ: 2,4
Слайд 29
Задание 6 тура (формулы)
Мощность прибора (в ватах) можно
вычислить по формуле
где U - напряжение питания (в вольтах),
а R - сопротивление прибора (в омах). Пользуясь этой формулой, найдите напряжение U , если R = 480 Ом, а P = 30 ВТ. Ответ дайте в вольтах.
Ответ:120
Слайд 30
Задание 6 тура (текстовая задача)
Площадь земель крестьянского хозяйства,
занятая под посадку сельскохозяйственных культур, составляет 24 га и
распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают зерновые культуры?
Ответ: 15 га
Слайд 31
Задание 6 тура (функции)
На рисунке изображен
график функции у
=f(х).
Какие из утверждений
относительно этой
функции неверны? Укажите их номера.
1)функция возрастает
на промежутке [-2;+∞)
2) f(3)> f(-2)
3) f(0)= -2
4)прямая у=2пересекает график в точках (-2;2) и (5;2)
Ответ: 1 3 4
Слайд 32
Задание 7 тура (уравнения)
Найдите корни уравнений:
а) 2х² + 11х – 6
= 0
б)
Ответы: а) 0,5; -6
б)-3
Слайд 33
Задание 7 тура (геометрическая задача)
В прямоугольном
треугольнике АВС
с прямым
углом С
известны катеты:
АС = 6, ВС = 8.
Найдите
медиану
СК этого треугольника
Медиана, проведённая из вершины прямого угла равна половине гипотенузы.
Ответ: 5
А
В
К
С
Слайд 34
Задание 7 тура (свойства числовых неравенств)
О числах а
и в известно, что -1
следующих неравенств неверны? Запишите их номера.
1) 0<-а<1 2) а+в <0 3) 1/в >1
Ответ: 2 3
Слайд 35
Задание 8 тура (последовательности)
В арифметической прогрессии, первый член
которой равен -3,4, а разность равна 3, найдите пятый
и одиннадцатый члены.
Решение:
Итак a1 = -3,4; d = 3. Для нахождения n-ого члена арифметической прогрессии воспользуемся формулой: an = a1 + (n-1)d. Имеем:
a5 = a1 + (5 – 1)d = -3,4 + 4 · 3 = 8,6;
a11 = a1 + (11 – 1)d = -3,4 + 10 · 3 = 26,6.
Ответ: 8,6 и 26,6
Слайд 36
Задание 8 тура (геометрия)
В прямоугольном
треугольнике АВС
с прямым углом
С
известны катеты:
АС = 6, ВС = 8.
Найдите радиус
окружности, вписанной в треугольник АВС
Радиус, вписанной в треугольник окружности, равен S:p.
Ответ: 1
А
В
С
6
8
?
Слайд 37
Задание 8 тура (алгебраические выражения)
Представить в виде дроби
выражение
и найдите его значение при х = 0,5. В
ответе запишите полученное число.
Ответ: -5
Слайд 38
Задание 9 тура (уравнения)
Решите уравнения
а)
б) х² + 7х - 18 = 0
Ответ: а) х = 24
б) х₁ = -9 х₂= 2
Слайд 39
Задание 9 тура (статистика и теория вероятностей)
На тарелке
лежат пирожки, одинаковые на вид: 8 с мясом, 4
с капустой и 3 с вишней. Катя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с вишней.
Ответ: 3/15 = 1/5
Слайд 40
Задание 9 тура (реальная математика)
Мальчик прошел от дома
по направлению на восток 550 м. Затем повернул на
север и прошел 480 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Ответ: 730 м
Слайд 41
Задание 10 тура (вычислите)
Найдите значения выражений. В ответе
укажите номер наибольшего из найденных значений.
1) 1,8 – 4/5
2) 1⅟7 : 4
3) (0,4 +1,7): 1,4
Ответ: 3 (т.к 1) 1; 2) 2/7; 3) 1,5)
Слайд 42
Задание 10 тура (задача)
Поступивший в продажу в январе
мобильный телефон стоил 3000 р. В марте он стал
стоить 2790 р. На сколько процентов снизилась цена на мобильный телефон в период с января по март?
Ответ: на 7%
Слайд 43
Задание 10 тура (формулы)
Площадь треугольника можно вычислить по
формуле
где в и с – стороны треугольника, а α
– угол между этими сторонами. Пользуясь этой формулой, найдите sin α, если S=9, с=3, в=8.
Ответ: 0,75