модуля с точки зрения геометрического смысла модуля и алгебраического
определения модуля.Научиться применять эти методы при решении уравнений, содержащих неизвестное под знаком модуля.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


















а
О
А
Расстояние от начало отсчета до точки, изображающей данное
число на числовой прямой, называется модулем этого числа.
Модуль числа а обозначается ׀а ׀
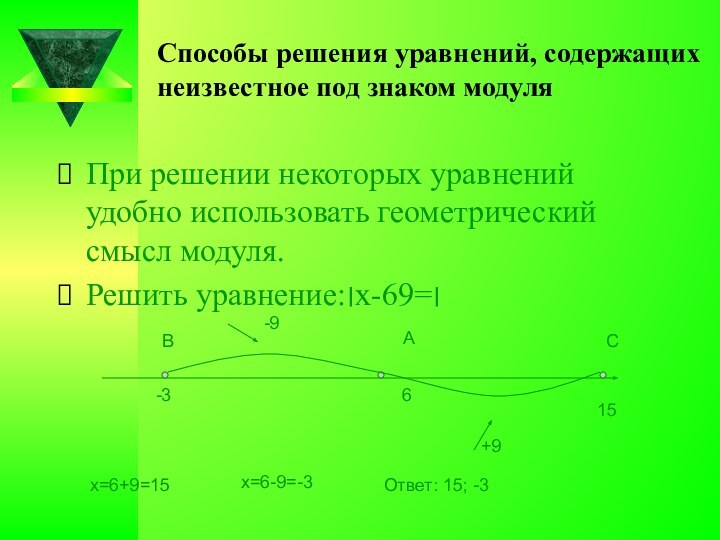
6
15
В
А
С
+9
-9
х=6+9=15
х=6-9=-3
Ответ: 15; -3
׀а׀=
а, если а≥0
-а, если а<0
-8
6
х
х<-8
-8<х<6
х>6
I
II
III
-(2х-12)+(6х+48)=160
-2х+12+6х+48=160
4х=100
х=25
число 25 не принадлежит данному промежутку
3
10
-4
+7
-7
-34
5
44
+39
-39
г) ׀ 28х-37׀=93
28х=37-93 28х=37+93
28х=-56 28х=130
х=-2 х=4 9/14
Ответ: -2; 4 9/14
84
+64
-64
37
+93
-93
-4
7
8
-4
10
7
24
-4
3
5