- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение систем неравенств 9 класс
Содержание
- 2. Математику нельзя изучать, наблюдая как это делает сосед.А. Нивен
- 3. ЗапомнимРешить систему неравенств – это значит найти значение переменной, при котором верно каждое из неравенств системы.
- 4. ЗапомнимЕсли надо решить систему неравенств, то:решаем каждое
- 5. СодержаниеРешение систем линейных неравенствРешение двойных неравенствРешение систем, содержащих квадратные неравенства
- 6. Решим систему неравенств (состоящую из линейных неравенств)
- 7. Решим систему неравенств
- 8. Работа в парах:Решить системунеравенств:1) 3х – 2
- 9. Примеры двойных неравенств Прочитайте неравенства:
- 10. Решение двойных неравенствРешить неравенство: 0< 4х
- 11. Решите неравенства, работая в парахРешить неравенства:-6
- 12. Решим систему неравенств (в которую входит квадратное
- 13. Решить систему неравенств:
- 14. Решим системы неравенств, работая вместе1)
- 15. Решите системы неравенств, работая самостоятельно1)
- 16. Скачать презентацию
- 17. Похожие презентации
Математику нельзя изучать, наблюдая как это делает сосед.А. Нивен















Слайд 3
Запомним
Решить систему неравенств – это значит найти значение
переменной, при котором верно каждое из неравенств системы.
Слайд 4
Запомним
Если надо решить систему неравенств, то:
решаем каждое неравенство
системы отдельно
изображаем полученные решения на числовой прямой и смотрим
пересечения этих решений.Эта общая часть и является решением данной системы неравенств.
Слайд 5
Содержание
Решение систем линейных неравенств
Решение двойных неравенств
Решение систем, содержащих
квадратные неравенства
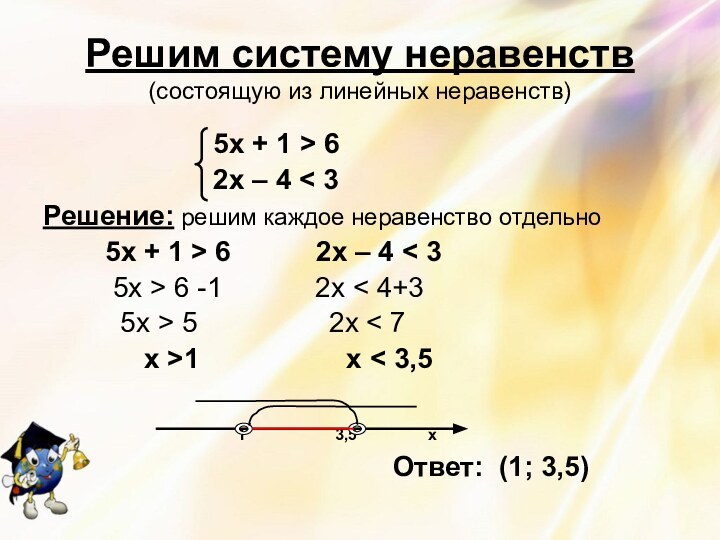
Слайд 6
Решим систему неравенств
(состоящую из линейных неравенств)
5х
+ 1 > 62х – 4 < 3
Решение: решим каждое неравенство отдельно
5х + 1 > 6 2х – 4 < 3
5х > 6 -1 2х < 4+3
5х > 5 2х < 7
х >1 х < 3,5
1 3,5 х
Ответ: (1; 3,5)
Слайд 7
Решим систему неравенств
5х + 12 ≤ 3х+ 20
х < 2х+3
2х + 7 ≥ 0
Решение: решим каждое неравенство отдельно
5х + 12 ≤ 3х+ 20 х < 2х+3 2х + 7 ≥ 0
5х – 3х ≤ - 12 + 20 х – 2х < 3 2х ≥ -7
2х ≤ 8 -х < 3 х ≥ -7/2
х ≤ 4 х > - 3 х ≥ -3,5
Изобразим на числовой прямой:
-3,5 -3 4
Ответ: ( -3; 4]
Слайд 8
Работа в парах:
Решить систему
неравенств:
1) 3х – 2 ≥
х + 1
4 – 2х ≤
х – 2 2) 3х > 12 + 11х
5х – 1 ≥ 0
Проверим ответы:
1) [2; +∞)
2) Нет решения
Слайд 10
Решение двойных неравенств
Решить неравенство: 0< 4х +2
≤ 6
Решение: составим систему: 4х
+ 2 > 04х + 2 ≤ 6
Решим каждое неравенство системы отдельно:
1) 4х + 2 > 0 2) 4х + 2 ≤ 6
х > - 0,5 х ≤ 1
Полученные результаты изобразим на числовой прямой:
-0,5 1 х
Ответ: -0,5 < х ≤ 1 или (-0,5; 1]
Слайд 11
Решите неравенства,
работая в парах
Решить неравенства:
-6 ≤ -
3х ≤ 3
4 < 2х – 1 ≤ 13
-2
≤ 6х + 7 < 1 0,3 < 0,5 + 0,1х < 0,6
0 < - 2х < 8
Проверим
ответы:
1) [-1; 2]
2) (2,5; 7]
3) [- 1,5; - 1)
4) (-2; 1)
5) (-4; 0)
Слайд 12
Решим систему неравенств
(в которую входит квадратное неравенство)
Решить систему
неравенств: х² - 5х + 4 ≤ 0
9 - 4х < 0Решение: решим каждое неравенство системы отдельно
1) х² - 5х + 4 ≤ 0 2) 9 - 4х < 0
х² - 5х + 4 = 0 - 4х < - 9
т.к. а+в+с=0, то х1=1; х2=4 х > 9/4=2,25
Полученные результаты изобразим на числовой прямой:
1 2,25 4 х
Ответ: [ 4; +∞)
+
-
-
Слайд 13
Решить систему неравенств:
х² - 3х +
2 < 02х² - 3х – 5 > 0
Решение: решим каждое неравенство отдельно
х² - 3х + 2 < 0 2х² - 3х – 5 > 0
Найдем корни соответствующих квадратных уравнений
х² - 3х + 2 = 0 2х² - 3х – 5 = 0
По свойствам коэффициентов имеем:
х1 = 1 х2 = 2 х1 = -1 х2 = 5/2= 2,5
Изобразим метод интервала на числовой оси:
-1 1 2 2,5 х
Ответ: (- ∞; -1) υ (2,5; +∞)
Решим систему неравенств
(в которую входит квадратное неравенство)
+
+
+
-
-
-
Слайд 14
Решим системы неравенств,
работая вместе
1) 6х² -
5х + 1 > 0
4х
– 1 ≥ 02) 4х² - 1 ≤ 0
х² > 1
3х² - 2х – 1 < 0
х² - х – 6 > 0
Слайд 15
Решите системы неравенств,
работая самостоятельно
1) х² -
10х + 9 ≥ 0
12 –
3х < 02) 2х²- 5х + 2 > 0
4х – 1 ≥ 3
3) 2х² - 7х + 5 < 0
2 – х ≥ 0
Проверим ответы:
1) (4; 9]
2) [1; 2)
3) (- ∞; 1)





























