- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Плоскость
Содержание
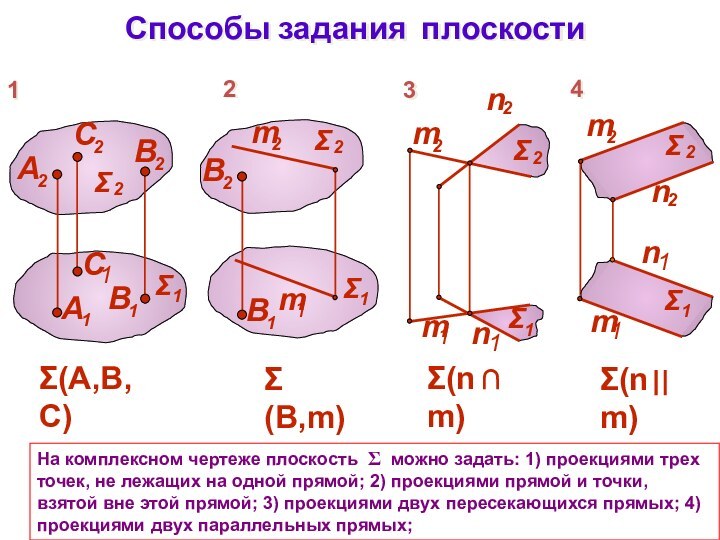
- 2. Способы задания плоскостиНа комплексном чертеже плоскость
- 3. Способы задания плоскости5) проекциями плоской фигурой; 6)
- 4. Положение плоскости относительно плоскостей проекцийПлоскость общего положения
- 5. Горизонтально проецирующая плоскость (П1)Пространственная картинаКомплексный чертежyzГоризонтальная проекция
- 6. Фронтально проецирующая плоскость (П2)Комплексный чертежyzПространственная картинаФронтальная проекция
- 7. Профильно проецирующая плоскость (П3)Комплексный чертежzПространственная картинаПрофильная проекция
- 8. Горизонтальная плоскость уровня ( П1)Комплексный чертежzПространственная картинаВ
- 9. Фронтальная плоскость уровня ( П2)Комплексный чертежzПространственная картинаВ
- 10. Профильная плоскость уровня ( П3)Комплексный чертежzПространственная картинаВ
- 11. Принадлежность прямой плоскостиПрямая принадлежит плоскости, если она
- 12. Принадлежность точки плоскостиТочка будет лежать в плоскости,
- 13. Принадлежность прямой и точки плоскостиЕсли плоскость занимает
- 14. Главные линии плоскостиГоризонталь плоскости – это прямая,
- 15. Главные линии плоскостиФронталей плоскости бесчисленное множество,все они
- 16. Главные линии плоскости П1x П2xВ проецирующих
- 17. А1А2При первом преобразовании выбираем новую плоскость проекций
- 18. xА1А2П1П4x1П4 П1 П4 h(АВС)
- 19. Метрические задачиЗадача 2.Определить расстояние от точки К
- 20. Метрические задачиА1А2Выбираем новую плоскость проекций П4
- 21. Скачать презентацию
- 22. Похожие презентации



Слайд 3
Способы задания плоскости
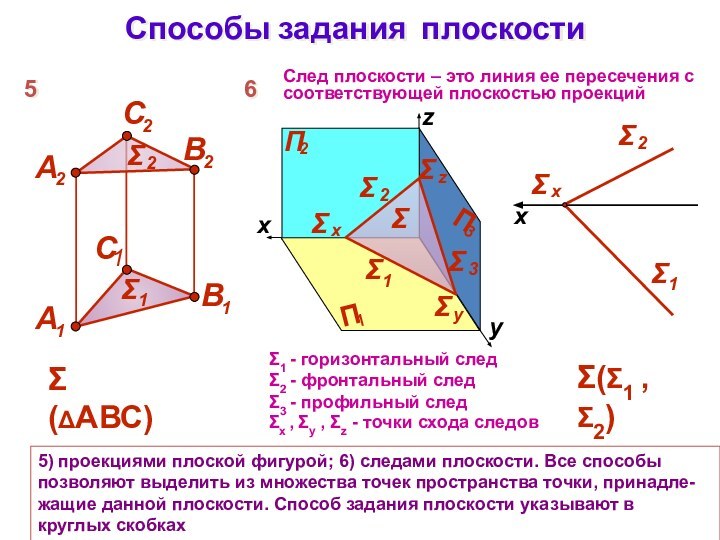
5) проекциями плоской фигурой; 6) следами
плоскости. Все способы позволяют выделить из множества точек пространства
точки, принадле-жащие данной плоскости. Способ задания плоскости указывают в круглых скобкахСлед плоскости – это линия ее пересечения с соответствующей плоскостью проекций
Слайд 4
Положение плоскости относительно плоскостей проекций
Плоскость общего положения наклонена
ко всем плоскостям проекций
Плоскость частного положения перпендикулярна или параллельна
одной из плоскостей проекций Горизонтально проецирующая плоскость П1
Фронтально проецирующая плоскость П2 Профильно проецирующая плоскость П3
Горизонтальная плоскость П1
Фронтальная плоскость П2
Профильная плоскость П3
Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью:
Плоскость, параллельная плоскости проекций, назы-вается плоскостью уровня (дважды проецирующей):
Слайд 5
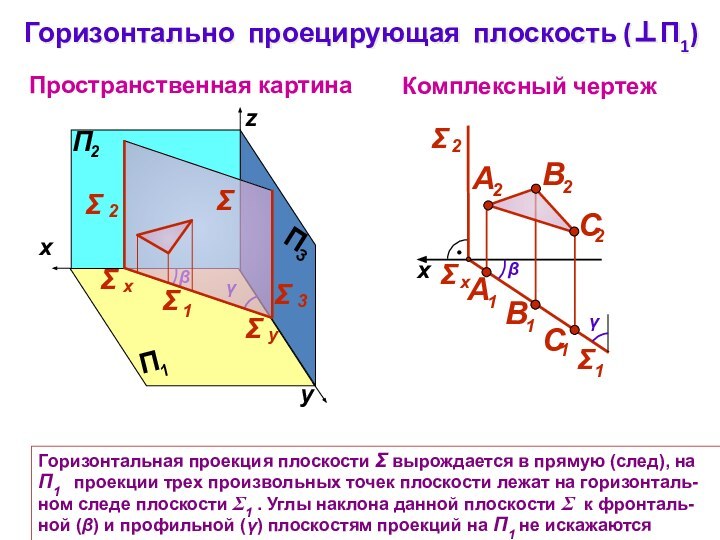
Горизонтально проецирующая плоскость (П1)
Пространственная картина
Комплексный чертеж
y
z
Горизонтальная проекция плоскости
вырождается в прямую (след), на П1 проекции
трех произвольных точек плоскости лежат на горизонталь-ном следе плоскости 1 . Углы наклона данной плоскости к фронталь-ной () и профильной () плоскостям проекций на П1 не искажаются
Слайд 6
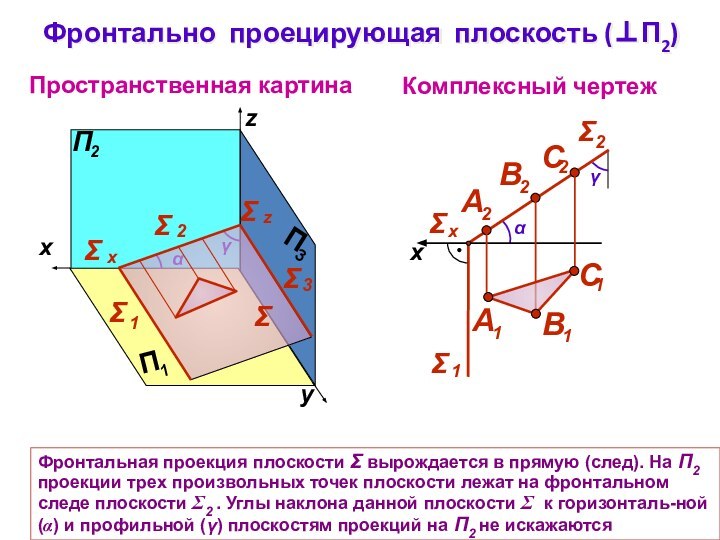
Фронтально проецирующая плоскость (П2)
Комплексный чертеж
y
z
Пространственная картина
Фронтальная проекция плоскости
вырождается в прямую (след). На П2 проекции трех
произвольных точек плоскости лежат на фронтальном следе плоскости 2 . Углы наклона данной плоскости к горизонталь-ной () и профильной () плоскостям проекций на П2 не искажаются
Слайд 7
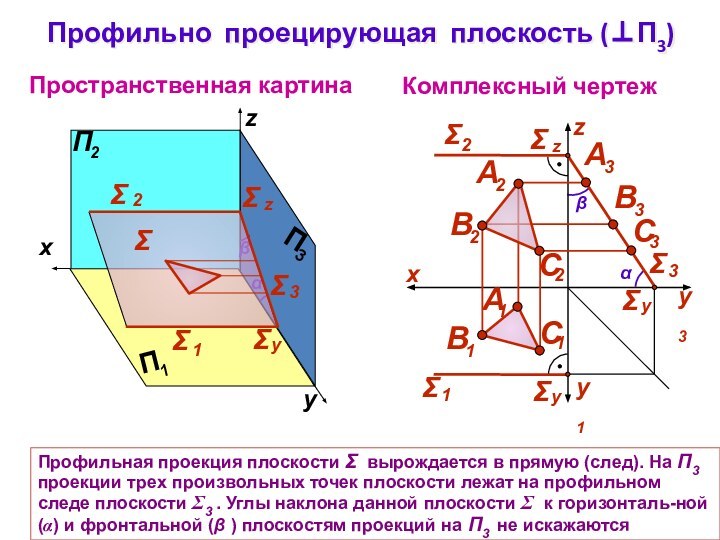
Профильно проецирующая плоскость (П3)
Комплексный чертеж
z
Пространственная картина
Профильная проекция плоскости
вырождается в прямую (след). На П3 проекции трех
произвольных точек плоскости лежат на профильном следе плоскости 3 . Углы наклона данной плоскости к горизонталь-ной () и фронтальной ( ) плоскостям проекций на П3 не искажаются
Слайд 8
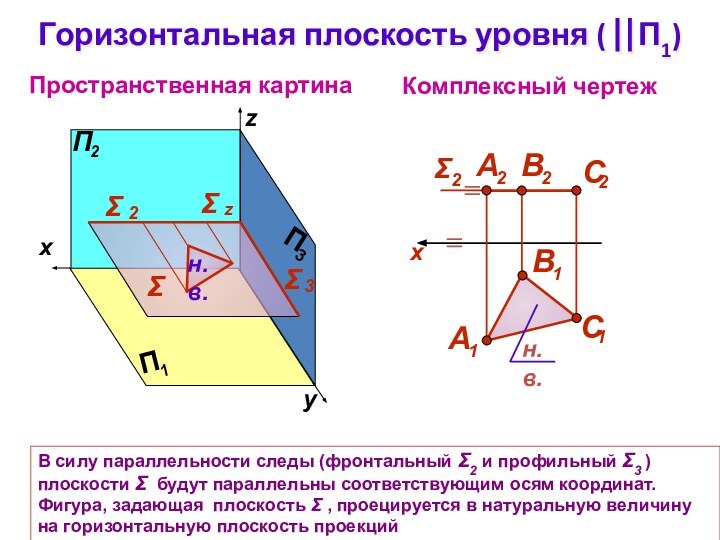
Горизонтальная плоскость уровня ( П1)
Комплексный чертеж
z
Пространственная картина
В силу
параллельности следы (фронтальный 2 и профильный 3 ) плоскости
будут параллельны соответствующим осям координат. Фигура, задающая плоскость , проецируется в натуральную величину на горизонтальную плоскость проекций
Слайд 9
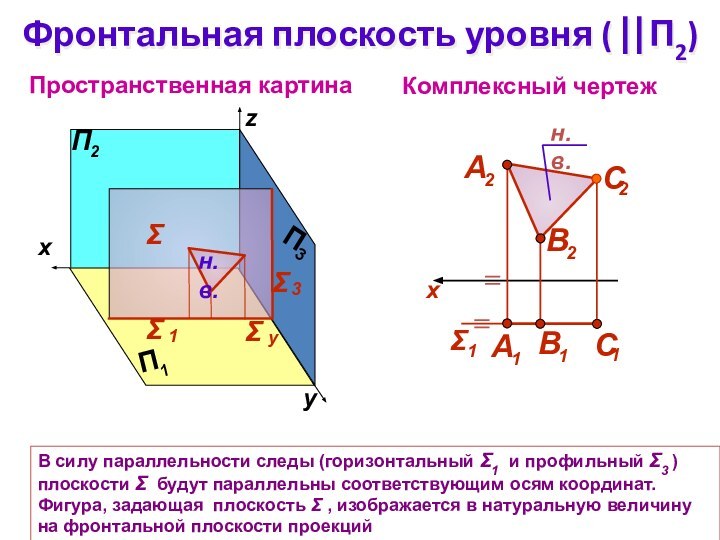
Фронтальная плоскость уровня ( П2)
Комплексный чертеж
z
Пространственная картина
В силу
параллельности следы (горизонтальный 1 и профильный 3 ) плоскости
будут параллельны соответствующим осям координат. Фигура, задающая плоскость , изображается в натуральную величину на фронтальной плоскости проекций
Слайд 10
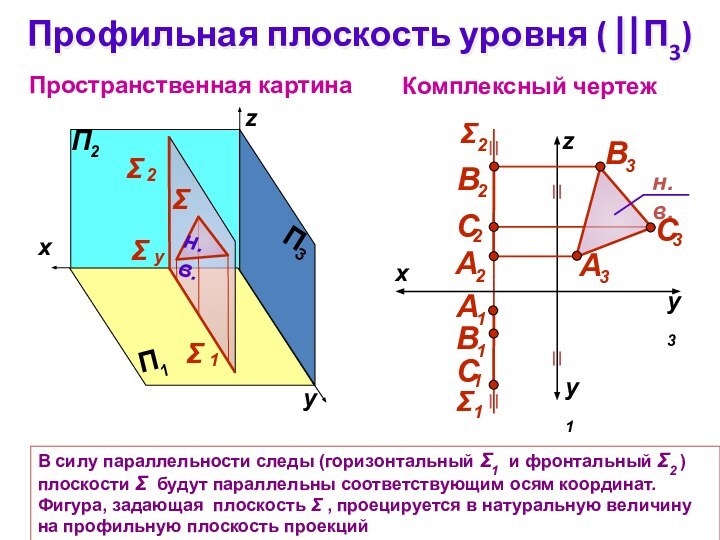
Профильная плоскость уровня ( П3)
Комплексный чертеж
z
Пространственная картина
В силу
параллельности следы (горизонтальный 1 и фронтальный 2 ) плоскости
будут параллельны соответствующим осям координат. Фигура, задающая плоскость , проецируется в натуральную величину на профильную плоскость проекций
Слайд 11
Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит:
через две точки этой плоскости;
2) через одну точку
плоскости и параллельно какой-нибудь прямой, лежащей в этой плоскости(n m)
1
(1m); (2n)
а(1 И 2) а
2
(n m)
(1m); 1b
b n b
Слайд 12
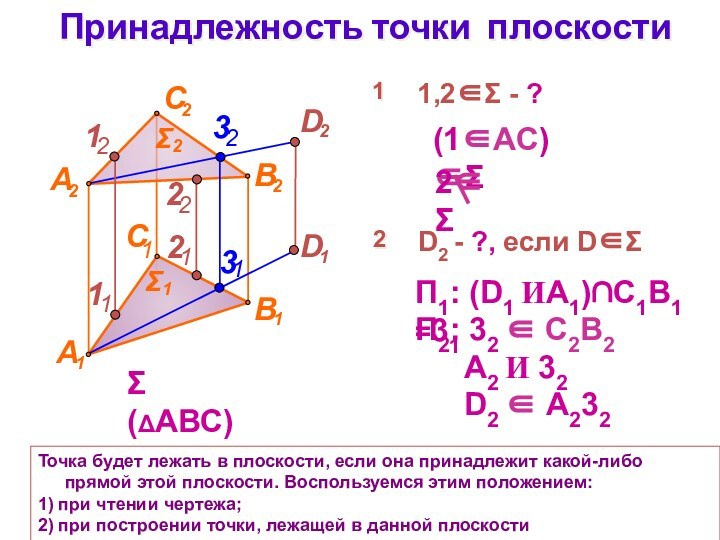
Принадлежность точки плоскости
Точка будет лежать в плоскости, если
она принадлежит какой-либо прямой этой плоскости. Воспользуемся этим положением:
1)
при чтении чертежа;2) при построении точки, лежащей в данной плоскости
(1АС)
П1: (D1 ИA1)С1В1 =31
(АВС)
1
П2: 32 C2B2
1,2 - ?
А2 И 32
D2 А232
Слайд 13
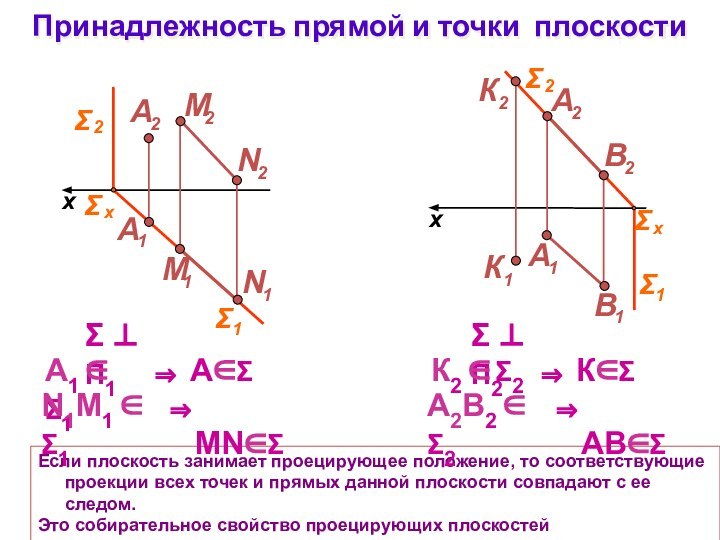
Принадлежность прямой и точки плоскости
Если плоскость занимает проецирующее
положение, то соответствующие проекции всех точек и прямых данной
плоскости совпадают с ее следом.Это собирательное свойство проецирующих плоскостей
П1
x
П2
x
Слайд 14
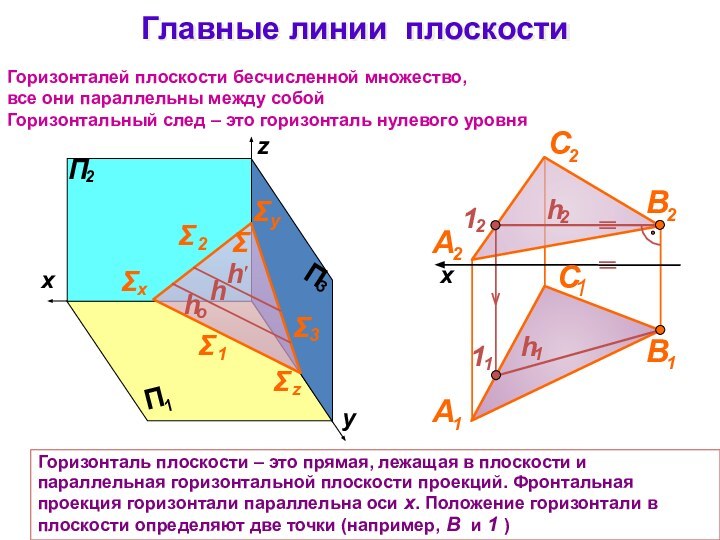
Главные линии плоскости
Горизонталь плоскости – это прямая, лежащая
в плоскости и параллельная горизонтальной плоскости проекций. Фронтальная проекция
горизонтали параллельна оси x. Положение горизонтали в плоскости определяют две точки (например, В и 1 )
Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня
x
Слайд 15
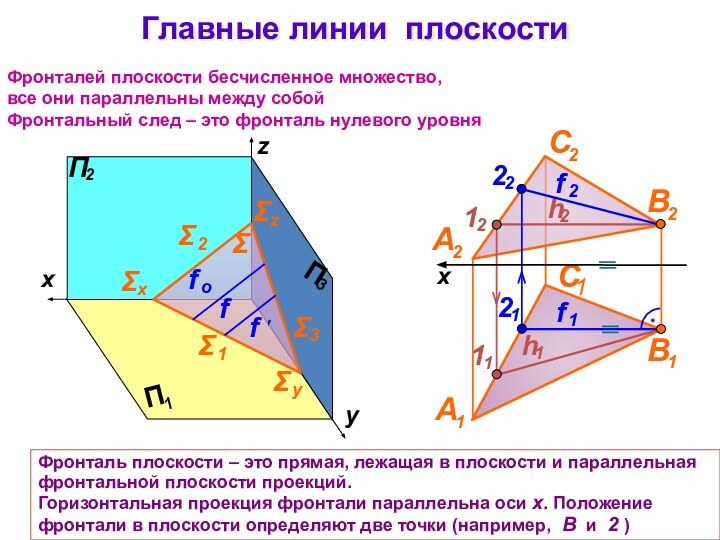
Главные линии плоскости
Фронталей плоскости бесчисленное множество,
все они параллельны
между собой
Фронтальный след – это фронталь нулевого уровня
Фронталь плоскости
– это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.Горизонтальная проекция фронтали параллельна оси x. Положение фронтали в плоскости определяют две точки (например, В и 2 )
x
Слайд 16
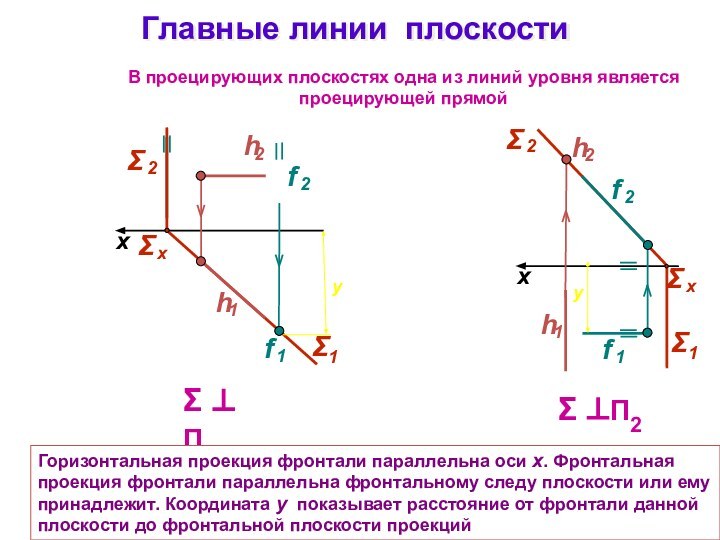
Главные линии плоскости
П1
x
П2
x
В проецирующих плоскостях
одна из линий уровня является проецирующей прямой
Горизонтальная проекция фронтали
параллельна оси x. Фронтальная проекция фронтали параллельна фронтальному следу плоскости или ему принадлежит. Координата y показывает расстояние от фронтали данной плоскости до фронтальной плоскости проекций
Слайд 17
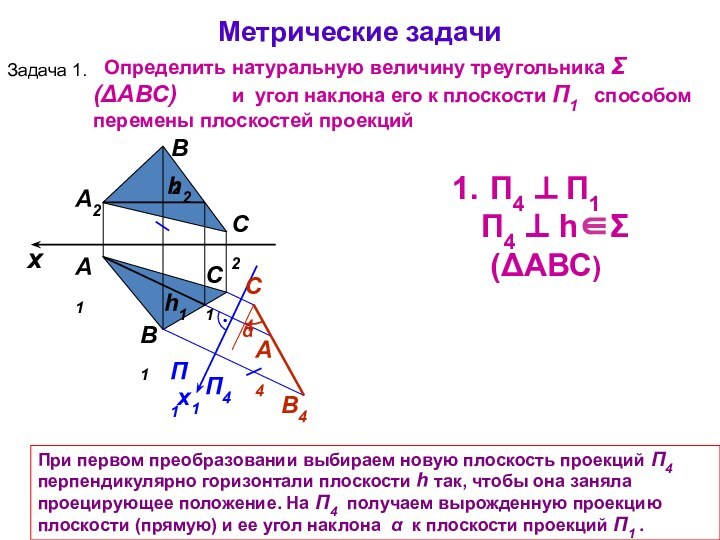
А1
А2
При первом преобразовании выбираем новую плоскость проекций П4
перпендикулярно горизонтали плоскости h так, чтобы она заняла
проецирующее положение. На П4 получаем вырожденную проекцию плоскости (прямую) и ее угол наклона к плоскости проекций П1 . Определить натуральную величину треугольника (АВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций
B1
C2
B2
C1
x
П4 П1
П4 h(АВС)
Метрические задачи
Задача 1.
Слайд 18
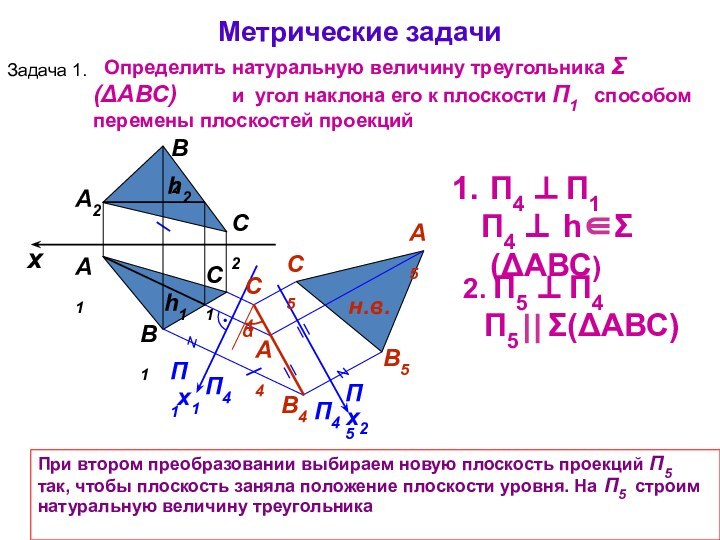
x
А1
А2
П1
П4
x1
П4 П1
П4 h(АВС)
2.
П5 П4
П5 (АВС)
При втором преобразовании
выбираем новую плоскость проекций П5 так, чтобы плоскость заняла положение плоскости уровня. На П5 строим натуральную величину треугольника h1
h2
B1
C2
B2
А4
C1
В4
C4
Метрические задачи
Задача 1.
Определить натуральную величину треугольника (АВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций
Слайд 19
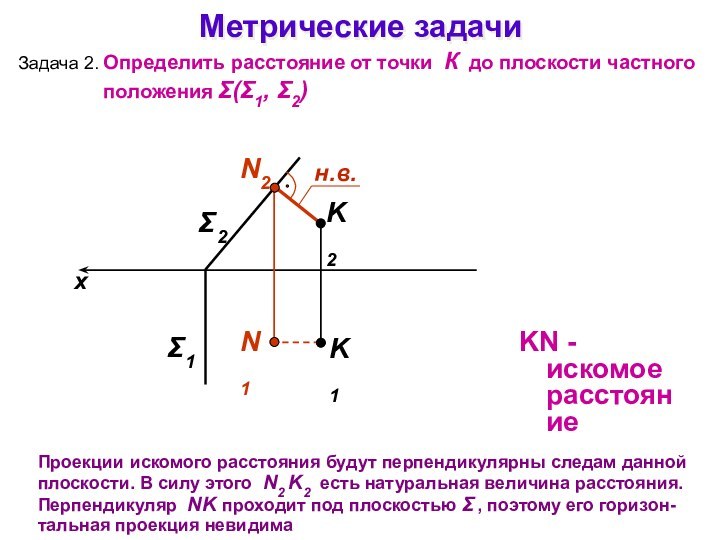
Метрические задачи
Задача 2.
Определить расстояние от точки К до
плоскости частного положения (1, 2)
x
Проекции искомого расстояния будут
перпендикулярны следам данной плоскости. В силу этого N2 K2 есть натуральная величина расстояния. Перпендикуляр NK проходит под плоскостью , поэтому его горизон-тальная проекция невидима 2
K1
1
K2
KN - искомое расстояние
Слайд 20
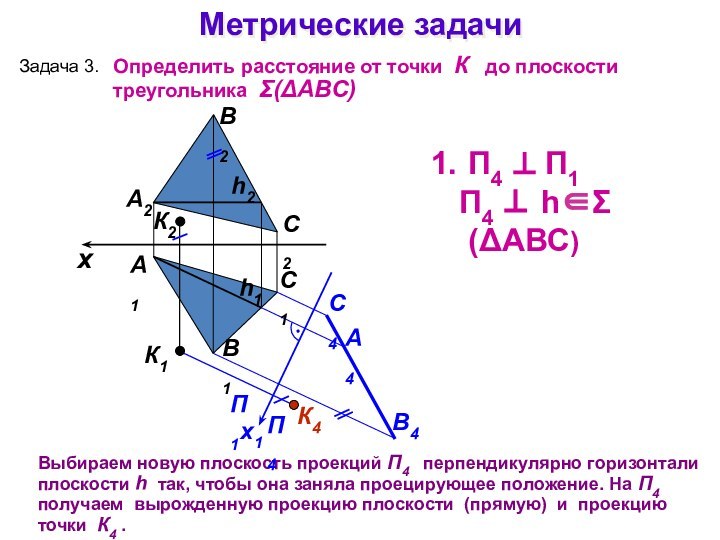
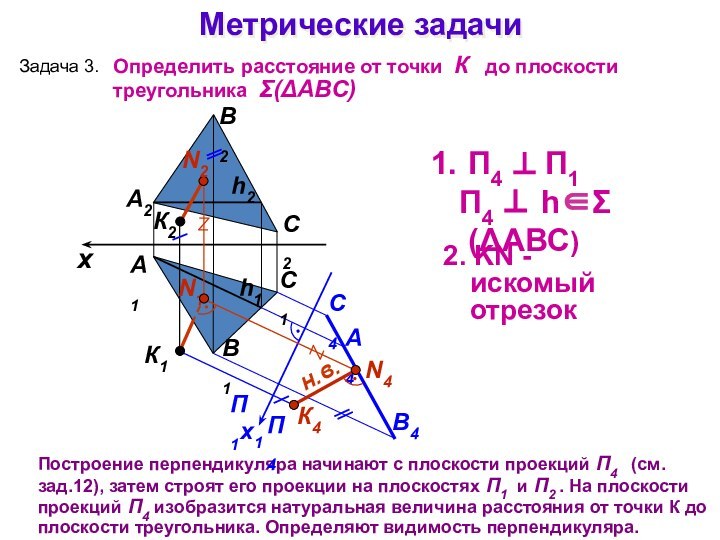
Метрические задачи
А1
А2
Выбираем новую плоскость проекций П4 перпендикулярно
горизонтали плоскости h так, чтобы она заняла проецирующее положение.
На П4 получаем вырожденную проекцию плоскости (прямую) и проекцию точки К4 .Задача 3.
B1
C2
B2
C1
x
П4 П1
П4 h(АВС)
К1
К2
Определить расстояние от точки К до плоскости треугольника (АВС)