Презентация на тему Решение системы линейных уравнений методом Крамера

содержит переменные только в первой степени и не содержит

произведений переменных.

Система m линейных уравнений с n переменными:

членами.
Совокупность чисел
называется решением системы линейных уравнений, если

при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.

сложения.

В курсе высшей математике решают методом Крамера ,методом

Гаусса и с помощью обратной матрицы.

Рассмотрим решение систем линейных уравнений методом Крамера

алгебры. Одной из самых известных его работ является «Введение

в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.

Женеве (Швейцария) в семье врача. Уже в детстве он

опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.

2 года Крамер выставил свою кандидатуру на должность преподавателя

в Женевском университете. Юноша так понравился магистрату, что специально для него и ещё одного одного кандидата на место преподавателя была учреждена отдельная кафедра математики, где Крамер и работал в последующие годы.

знаменитых математиков своего времени – Иоганна Бернулли и Эйлера

в Базеле, Галлея и де Муавра в Лондоне, Мопертюи и Клеро в Париже и других. Со многими из них он продолжал переписываться всю жизнь.
В 1729 году Крамер возобновляет преподавательскую работу в Женевском университете. В это время он участвует в конкурсе Парижской Академии и занимает второе место.

темы: геометрия, история, математика, философия. В 1730 году он

опубликовал труд по небесной механике.

к печати сборник своих работ. В 1742 году Крамер

публикует сборник в 4-х томах. В 1744 году он выпускает посмертный сборник работ Якоба Бернулли (брата Иоганна Бернулли), а также двухтомник переписки Лейбница с Иоганном Бернулли. Эти работы вызвали большой интерес со стороны учёных всего мира.

Габриэль Крамер скончался 4 января 1752 года во Франции

то система линейных уравнений имеет одно единственное решение, причём

неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

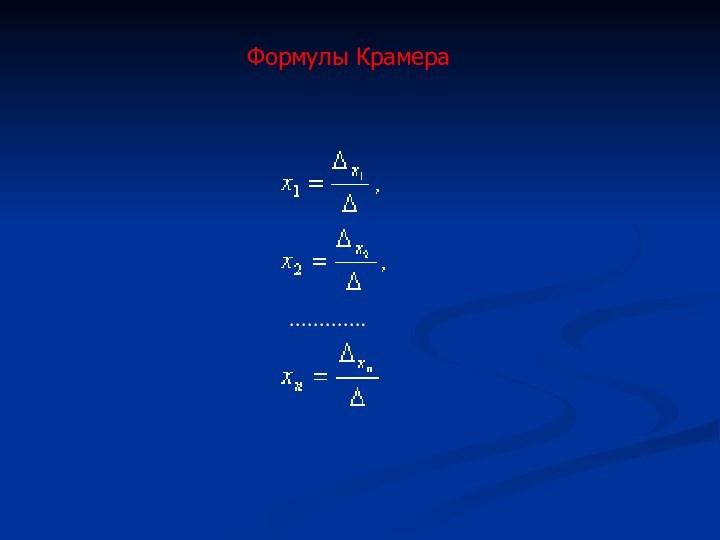
Решение системы линейных уравнений методом Крамера

методом Крамера

         Ответ: (1;-1)
1)

2)  Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн усл. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго – на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?

Решение. Пусть x и y – прибыли первого и второго отделений в минувшем году. Тогда условие задачи можно записать в виде системы:

Решив систему, получим x = 4, y = 8.

Ответ: а) прибыль в минувшем году первого отделения - 4 млн усл. ед., второго - 8 усл.ед.

б) прибыль в этом году первого отделения 1,7. 4 = 6,8 млн усл. ед.,

второго 1,4. 8 = 11,2 млн усл. ед.

и определённа)
Условия:

При решении системы уравнений могут встретиться три случая:

совместна и неопределённа)
Условия:
т.е. коэффициенты при неизвестных и свободные члены

пропорциональны

называется несовместной, если у неё нет ни одного решения,

и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

неизвестными методом Крамера


Решение. Находим определители системы: