Презентация на тему Решение транспортной задачи в среде Maple

условия разрешимости транспортной задачи
Опорное решение транспортной задачи. Циклы
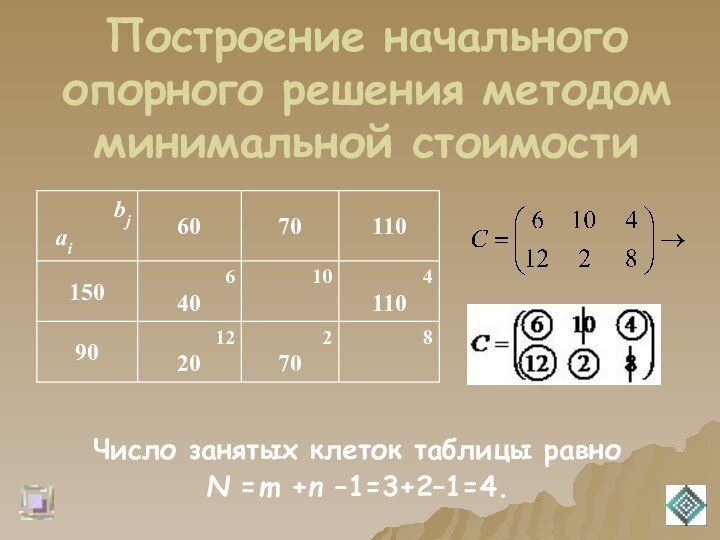
Построение начального

опорного решения методом минимальной стоимости
Переход от одного опорного решения к другому
Метод потенциалов
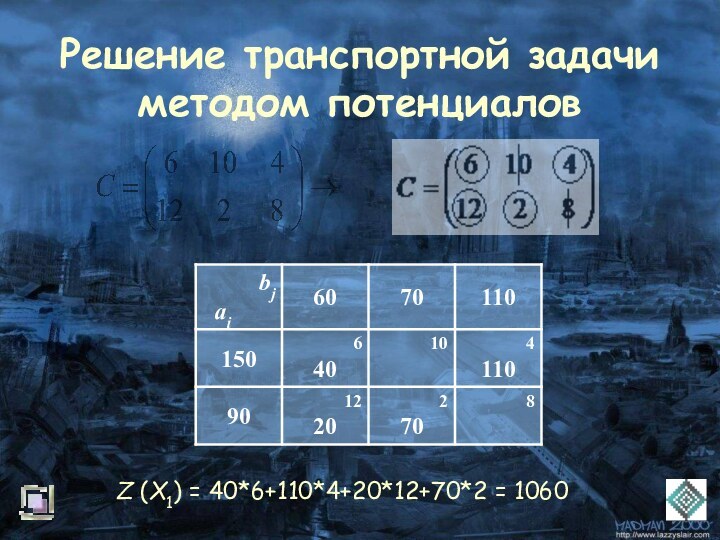
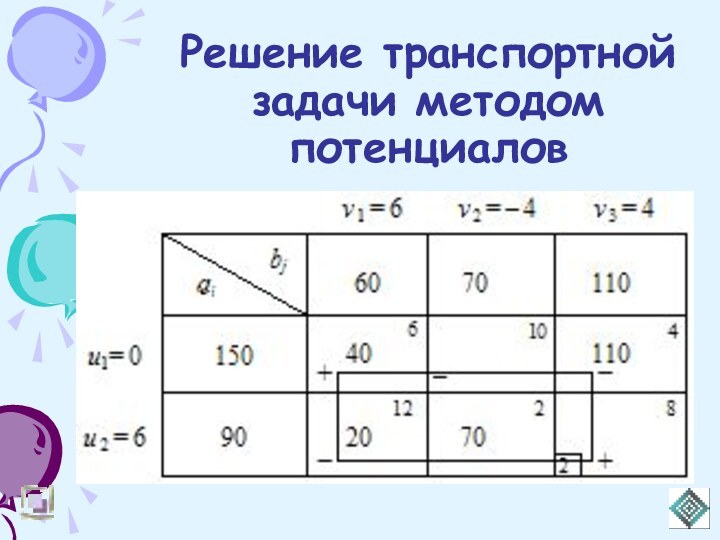
Решение транспортной задачи методом потенциалов
Решение транспортной задачи в среде Maple

5x12 + 7x13 + 4x21 + 6x22 + 10x23

Теорема. Для того чтобы транспортная задача линейного программирования имела

решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запасам потребителей:

т.е. задача должна быть с правильным балансом.
Ранг системы векторов-условий транспортной задачи равен N =m +n –1.

(о взаимосвязи линейной зависимости векторов-условий и возможности образования цикла).

Для того, чтобы система векторов-условий транспортной задачи была линейно зависимой, необходимо и достаточно, чтобы из соответствующих клеток таблицы можно было выделить часть, которая образует цикл.
Следствие. Допустимое решение транспортной задачи X = (xij), i =1, 2, ..., m, j =1, 2, ..., n является опорным тогда и только тогда, когда из занятых им клеток таблицы нельзя образовать ни одного цикла.

Теорема. Решение транспортной задачи, построенное методом минимальной стоимости, является

опорным.

клеток таблицы равно N =m +n –1=3+2–1=4.

Теорема ( о существовании и единственности цикла). Если таблица

транспортной задачи содержит опорное решение, то для любой свободной клетки таблицы существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением.
Цикл называется означенным, если его угловые клетки пронумерованы по порядку и нечетным клеткам приписан знак «+», а четным знак «–».

допустимое решение X = (xij ), i = 1,

2, ..., m, j = 1, 2, ..., n транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков ui, i = 1, 2, …, m и потребителей vj, j = 1, 2, …, n, удовлетворяющие следующим условиям:
ui + vj = cij при xij > 0,
ui + vj ≤cij при xij = 0.
Δij = ui +vj –cij при xij =0

Опорное решение является оптимальным, если для всех векторов-условий (клеток таблицы) оценки неположительные.

= 1060

–c12 = 0–4–10 = –14
Δ23 = u2 +v3 –c23

= 6+4–8 = 2.

*6+90 *4+70 *2+20 *8 = 1020

заданной системы уравнений или неравенств к стандартной форме неравенств

типа «меньше или равно».
minimize - вычисление минимума функции;
simplify (expr, n1, n2, …) – возвращает упрощенное выражение expr с учетом параметров с именами n1, n2, … (в том числе заданных списком или множеством);

решения транспортной задачи в программе Maple 7 имена ячеек

должны быть указаны в виде х11, х12 и т.д.

into List.
[-x11-x21

x12+x22<=70,-x12-x22<=-70];

x12+x22

[x13=90, x22=70, x23=20, x11=60, x12=0, x21=0]);