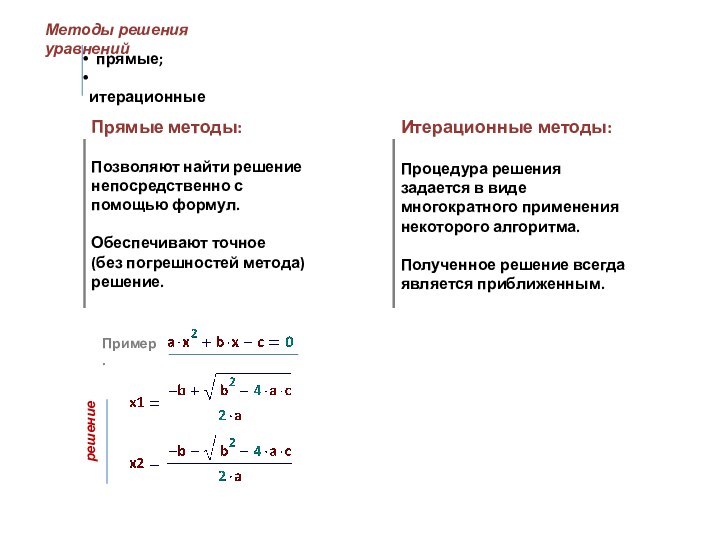
решение непосредственно с помощью формул.
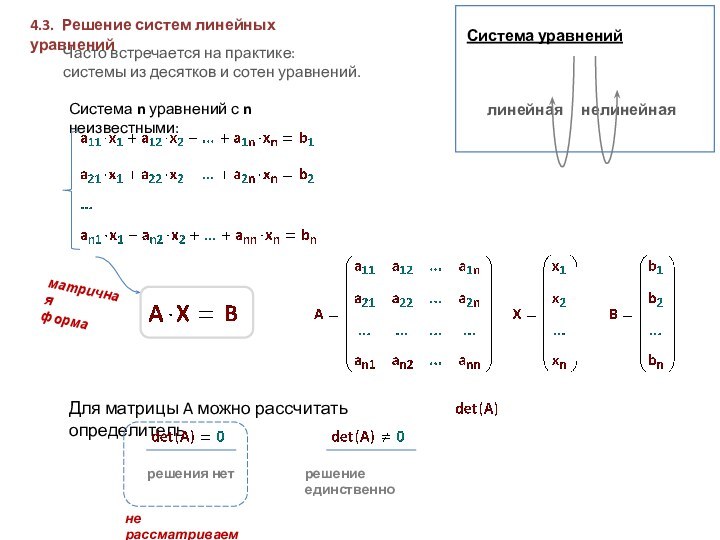
Обеспечивают точное
(без погрешностей
метода) решение.Итерационные методы:
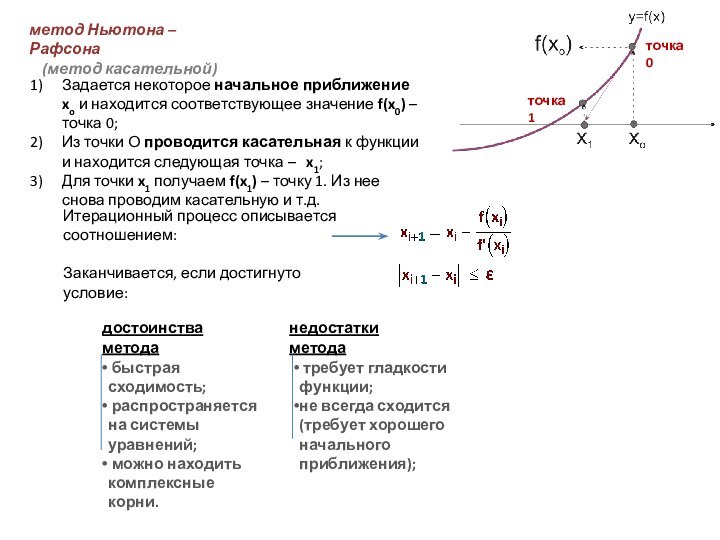
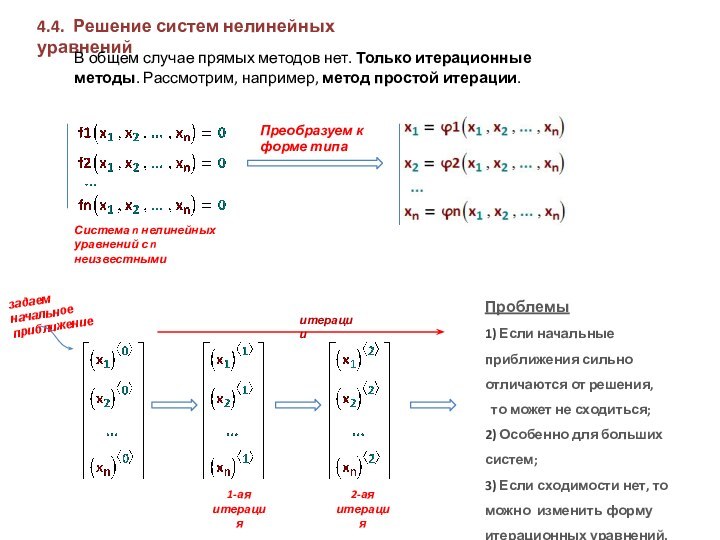
Процедура решения задается в виде многократного применения некоторого алгоритма.
Полученное решение всегда является приближенным.
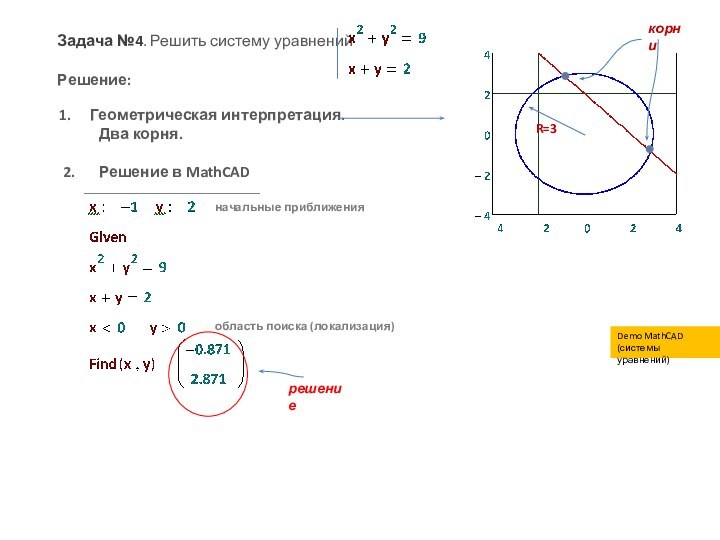
Пример.
решение