- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение задач с помощью квадратных уравнений
Содержание
- 2. «Математика - гимнастика ума» Александр
- 3. И г р а «Дешифровщик»
- 4. И г р а «Дешифровщик»В а р
- 5. И г р а «Дешифровщик»
- 6. Решить задачу: Две группы разведчиков отправились
- 7. Р е ш е н и е:Пусть
- 8. Группа разведчиков. Северо-Западный фронт, 1941 г, вторая мировая война.
- 9. Квадратное уравнение как математическая модель текстовой
- 10. Самостоятельная работа.В а р и а н
- 11. Проверка:В а р и а н т
- 12. Итоги урока.– Какие этапы выделяют при решении
- 13. Домашнее задание:№ 569, № 572, № 578 (б),Дополнительно (для желающих): № 570.
- 14. МОЛОДЦЫ!СПАСИБО ЗА УРОК !
- 15. Скачать презентацию
- 16. Похожие презентации















Слайд 3
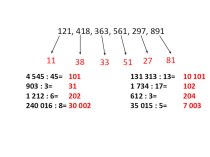
И г р а «Дешифровщик»
Мобильный высокоточный оперативно-тактический ракетный комплекс (ОТРК) предназначен
для скрытной подготовки и нанесения эффективных ракетных ударов по особо важным малоразмерным и площадным целям в глубине оперативного построения войск противника: огневым средствам (ракетные комплексы , дальнобойная артиллерия), самолетам и вертолетам на аэродромах, командным пунктам и узлам связи, важнейшим объектам гражданской инфраструктуры.Вы узнаете, как называется этот комплекс, если правильно выполните все задания и составите слово из полученных букв.
Выполнить задания по вариантам: первый вариант получает первую, третью, пятую и седьмую буквы данного слова, а второй – вторую, четвёртую, шестую и восьмую.
Слайд 4
И г р а «Дешифровщик»
В а р и
а н т 1 В а
р и а н т 22х2 – 18= 0; (1) х2 +3х= 0; (2)
5х2 – 4х – 1 = 0; (3) 3х2 – 5х + 2 = 0; (4)
х2 – 6х + 9 = 0; (5) 4х2 – 4х + 1 = 0; (6)
3х – х2 + 10 = 0; (7) 2х – х2 + 3 = 0; (8)
Слайд 5
И г р а «Дешифровщик»
Особенности комплекса: ОТРК "Искандер" создан с использованием современных научно-технических и конструкторских достижений в области разработки оперативно-тактических ракетных комплексов. По совокупности реализованных технических решений, высокой боевой эффективности сегодня он является высокоточным оружием нового поколения, которое по своим тактико-техническим характеристикам превосходит существующие отечественные ракетные комплексы "Скад-Б", "Точка-У", а также зарубежные аналоги Lance, ATACMS, Pluton и другие.
Слайд 6
Решить задачу:
Две группы разведчиков отправились одновременно
из одного пункта – одна на север со скоростью
4 км/ч, а другая на запад со скоростью 5 км/ч. Через какое время расстояние между группами окажется равным 16 км.
Слайд 7
Р е ш е н и е:
Пусть t
ч – время, через которое расстояние между
группами будет 16
км. За это время один разведчикпрошёл на север 4t км, а второй на запад 5t км.
Расстояние между ними равно длине отрезка АВ и
вычисляется по теореме Пифагора:
(АВ)2 = (АС)2 + (ВС)2.
Зная, что длина отрезка АВ равна 16 км, составляем уравнение:
(16)2 = (5t)2 + (4t)2;
256 = 25t2 + 16t2;
41t2 = 256;
t2 = 256/41
t ≈ ±2,5.
Так как время выражается положительным числом, то
t ≈ –2,5 не удовлетворяет условию задачи.
О т в е т: ≈ 2,5 ч.
Слайд 9
Квадратное уравнение как математическая
модель текстовой задачи.
Выделим этапы решения
задачи алгебраическим методом:
1. Анализ условия задачи и его схематическая
запись.2. Перевод естественной ситуации на математический язык (построение математической модели текстовой задачи).
3. Решение уравнения, полученного при построении математической модели.
4. Интерпретация полученного решения.
Слайд 10
Самостоятельная работа.
В а р и а н т
1
Одну сторону смотровой площадки полигона (квадратной формы) уменьшили на
2 м, а другую – на 1 м и получили участок прямоугольной формы площадью 6 м2. Найдите длину стороны первоначальной площадки. В а р и а н т 2
Одну сторону смотровой площадки полигона (квадратной формы) увеличили на 2 м, а другую – на 1 м и получили участок прямоугольной формы площадью 12 м2. Найдите длину стороны первоначальной площадки.
Площадка на военном полигоне — это обычно единый ограниченный участок полигона, предназначенный для какой-то конкретной деятельности (хозяйственной, испытательной, жилой, учебной). Обычно площадка огораживается колючей проволокой, реже забором, и имеет один или несколько контрольно-пропускных пунктов (КПП). На площадке управления может размещаться целая войсковая часть, а на испытательных площадках могут находиться объекты испытаний, помещения для инженерно-технических служб, измерительные комплексы.
Слайд 11
Проверка:
В а р и а н т 1.
Пусть
х м – первоначальная сторона, тогда (х – 2)м
и (х – 1) м – стороны полученной площадки.Зная, что площадь полученной
площадки равна 6 м2, составим
уравнение:
(х – 2) (х – 1) = 6;
х2 – х – 2х + 2 – 6 = 0;
х2 – 3х – 4 = 0;
D = (–3)2 – 4 · 1 · (–4) = 9 + 16 = 25;
D > 0; 2 корня.
x1 = 4; x2 = –1.
Так как длина стороны выражается
положительным числом, то х2 = –1 – не удовлетворяет условию задачи.
О т в е т: 4 см.
В а р и а н т 2.
Пусть х м – первоначальная сторона, тогда (х + 2)м и (х + 1) м – стороны полученной площадки.
Зная, что площадь полученной
площадки равна 12 м2, составим
уравнение:
(х + 2) (х + 1) = 12;
х2 + х + 2х + 2 – 12 = 0;
х2 + 3х – 10 = 0;
D = 32 – 4 · 1 · (–10) = 9 + 40 = 49;
D > 0; 2 корня.
x1 = 2; x2 = –5.
Так как длина стороны выражается
положительным числом, то х2 = –5 – не удовлетворяет условию задачи.
О т в е т: 2 см.
Слайд 12
Итоги урока.
– Какие этапы выделяют при решении задачи
алгебраическим методом?
– В чём состоит интерпретация полученного решения задачи?
–
Когда полученное решение может противоречить условию задачи?– Какие решения, полученные на сегодняшнем уроке, вы интерпретировали как противоречащие условию задачи?