- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Скалярное произведение в координатах
Содержание
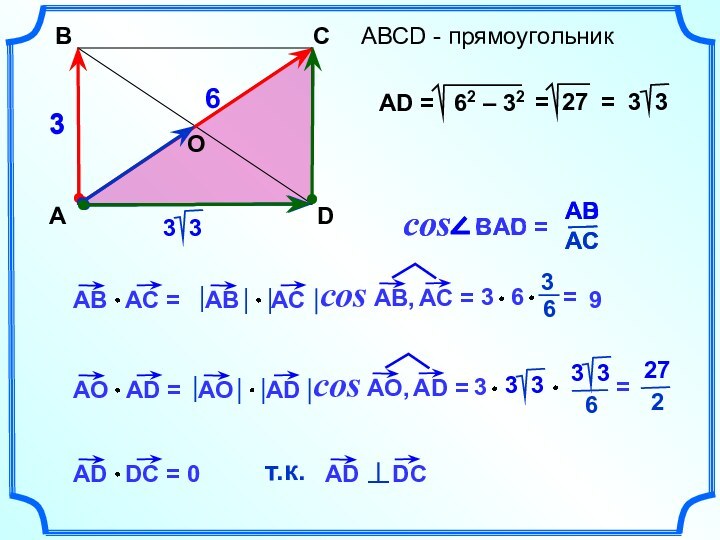
- 2. АВСD - прямоугольникABCD369O30
- 3. Теорема= x1x2 + y1y2Случай, когда один из векторов нулевойДоказательство:
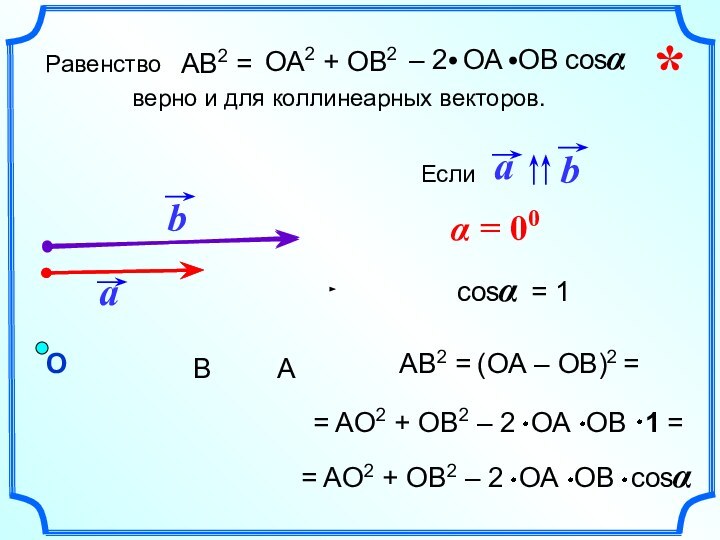
- 4. *
- 5. α = 00AB2 = (ОА – ОВ)2 ==
- 6. α = 1800AB2 = (ОА + ОВ)2
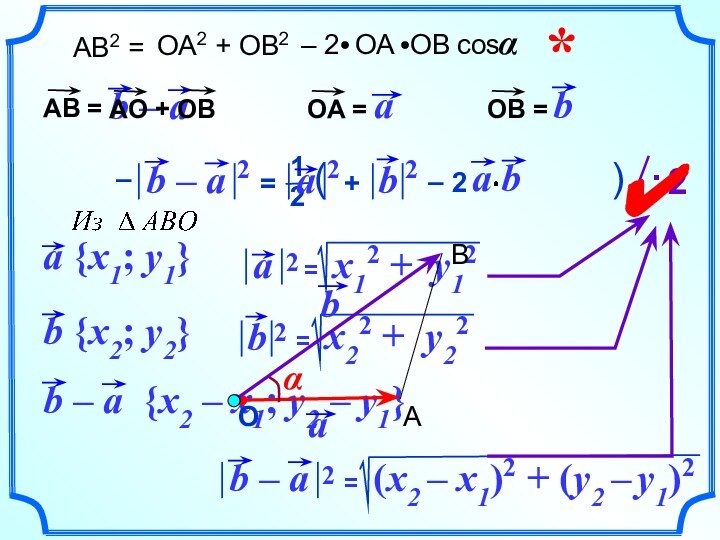
- 7. =*– – 2 2 22
- 8. 2Ненулевые векторы и
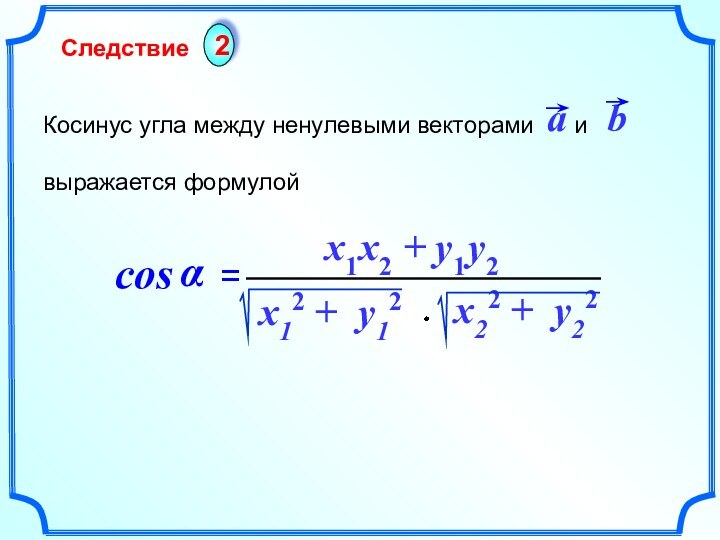
- 9. Косинус угла между ненулевыми векторами и выражается формулойСледствие2x1 x2 + y1 y2
- 10. Следствие2Доказательство: = x1x2 + y1y2 x1x2 + y1y2
- 11. Сочетательный законПереместительный законРаспределительный закон123Свойства скалярного произведения векторов4причем
- 12. Обоснуем
- 13. = x1x2 + y1y2=x2+x1y1y2Переместительный закон
- 14. = x1 x3 +
- 15. Рассмотрим векторы = (k x1) x2 +
- 16. Распределительный закон имеет место для любого числа слагаемых. Например,
- 17. Найдите c {-2;-1,5}= - 10 = 2,5 = 0 тупойострыйпрямой
- 18. x = 2*x+ -21 4=
- 19. Найдите c {-2;-1,5}= 4 = - 1,5 = 0 острыйтупойпрямой{ 1; 0}{ 0; 1}
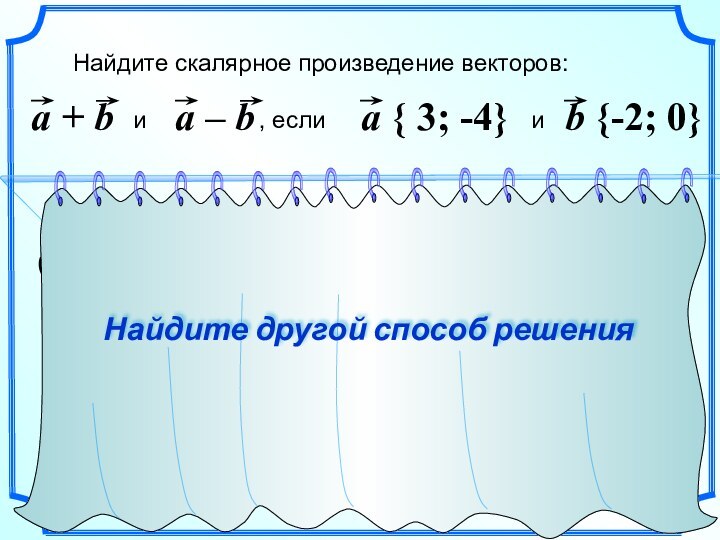
- 20. Найдите скалярное произведение векторов:
- 21. Найдите скалярное произведение векторов:
- 22. Найдите скалярное произведение векторов:
- 23. Вычислить
- 25. Скачать презентацию
- 26. Похожие презентации
АВСD - прямоугольникABCD369O30


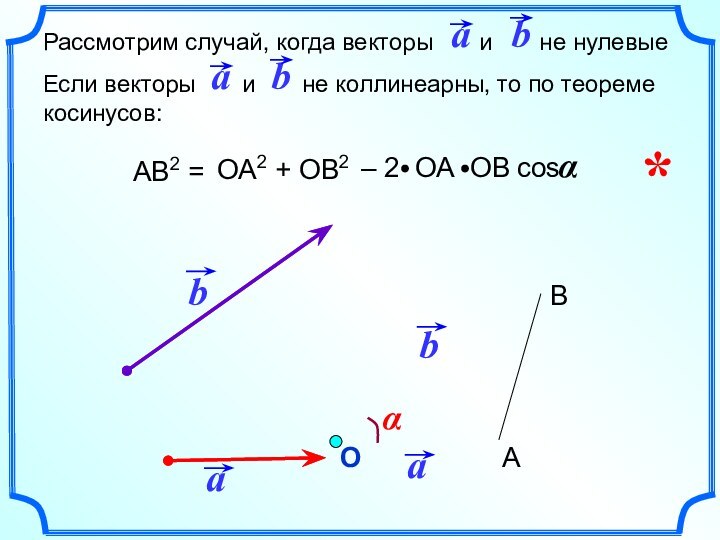
















Слайд 8
2
Ненулевые векторы и
перпендикулярны тогда и
только тогда, когда
x1
x2 + y1 y2 = 0Следствие
1
⇔
x1 x2 + y1 y2 = 0
Пример
+
-2
1
4
= 0
Слайд 11
Сочетательный закон
Переместительный закон
Распределительный закон
1
2
3
Свойства скалярного произведения векторов
4
причем
при
Слайд 14 = x1 x3 +
+ + y2 y3 =
(
) ( )Рассмотрим векторы
= (x1 + x2) x3 + (y1 + y2) y3 =
Распределительный закон
x2 x3
y1 y3
Слайд 21
Найдите скалярное произведение векторов:
и
, если и1
2
3
1
2
3
(a + b)(a – b) = 1 5 + (-4) (-4) = 21
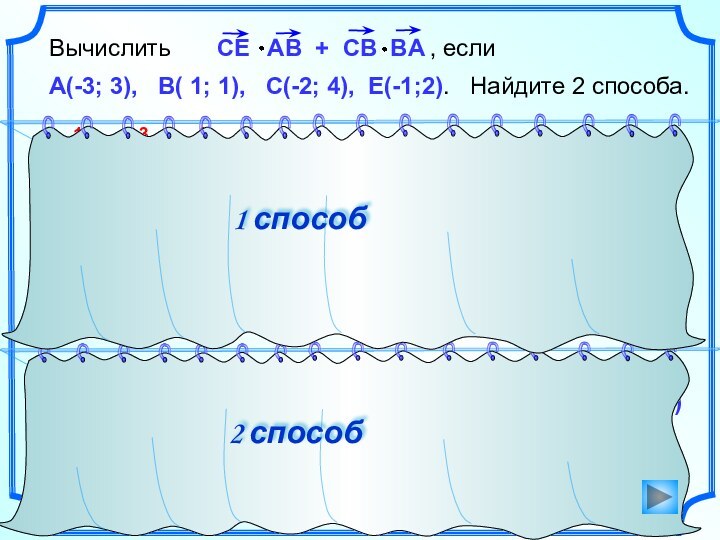
Слайд 23 Вычислить
, если
А(-3; 3), В( 1; 1), С(-2; 4), Е(-1;2). Найдите 2 способа.
1
2
3
1
2
3
8 + (-18) = -10