Презентация на тему Решение задач В8 ЕГЭ по математике

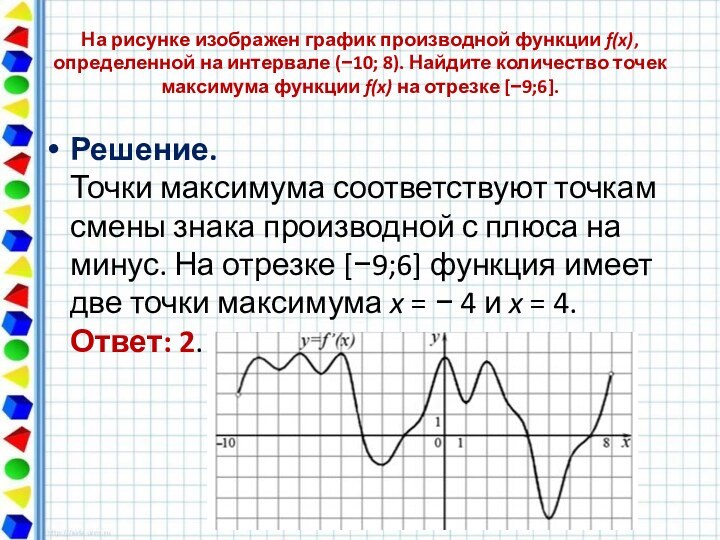
плюса на минус. На отрезке [−9;6] функция имеет две

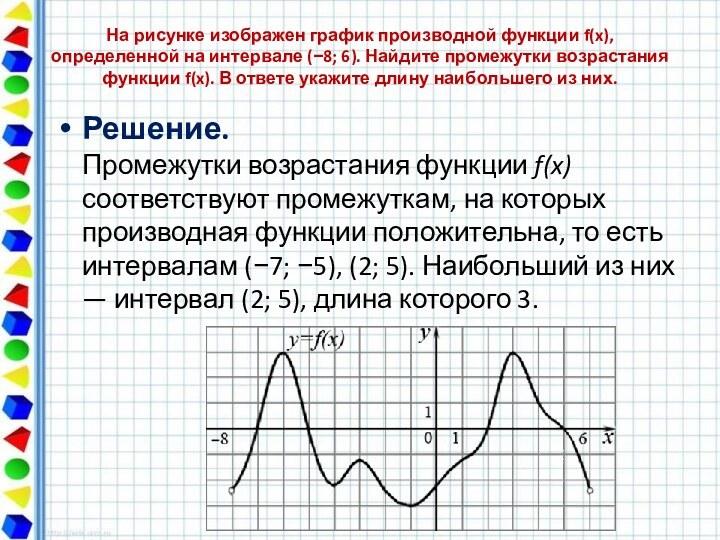
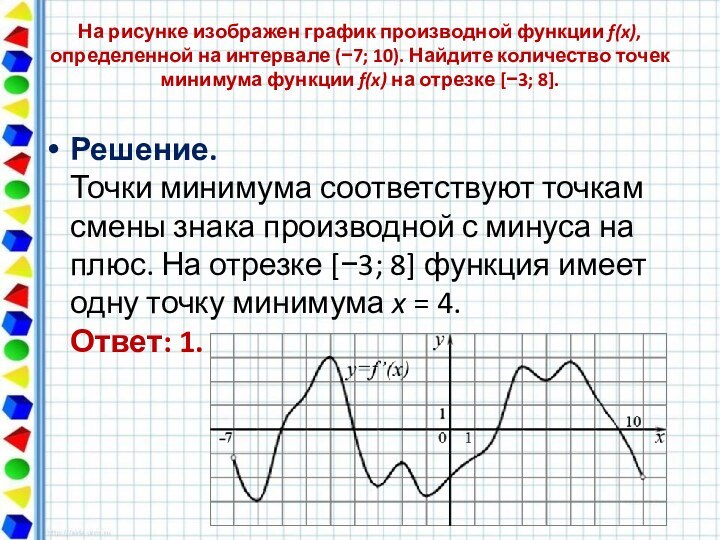
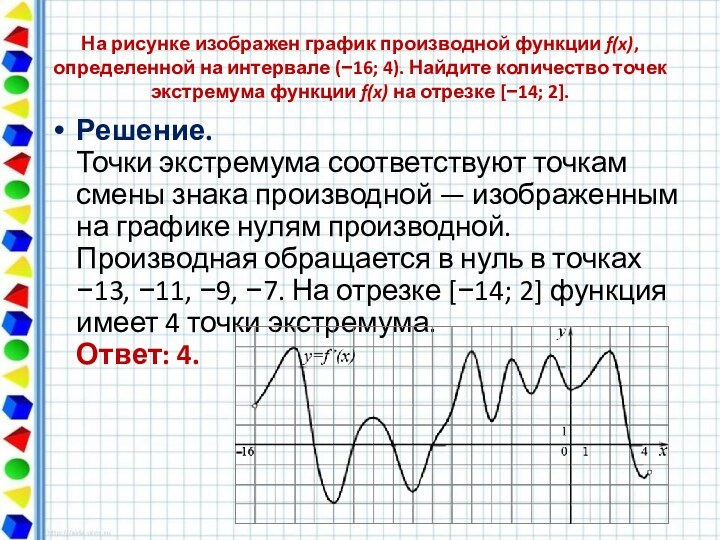
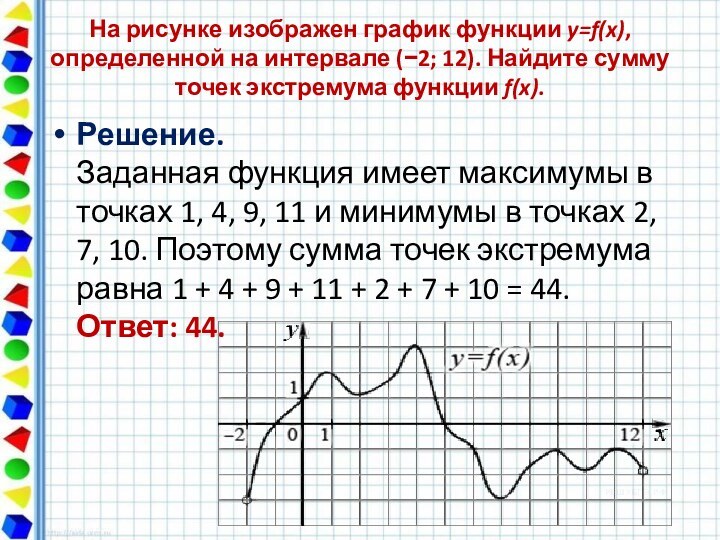
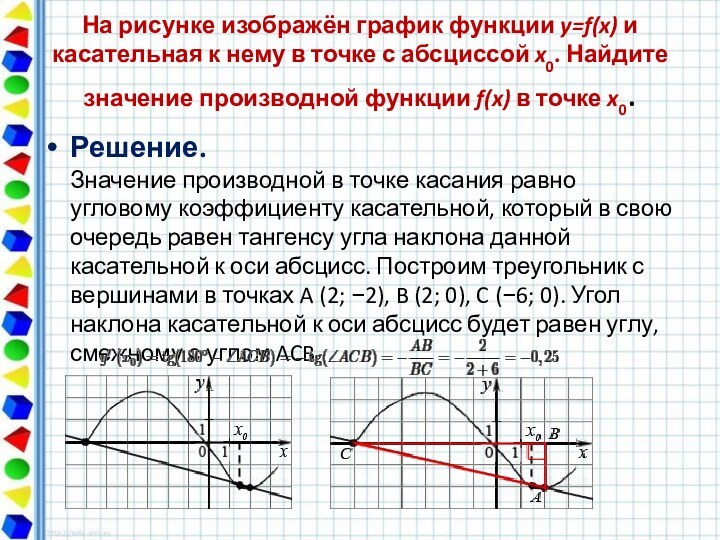
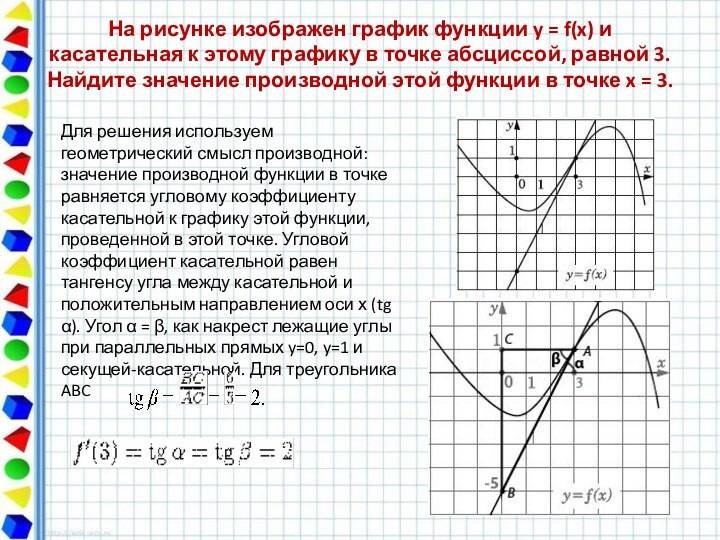
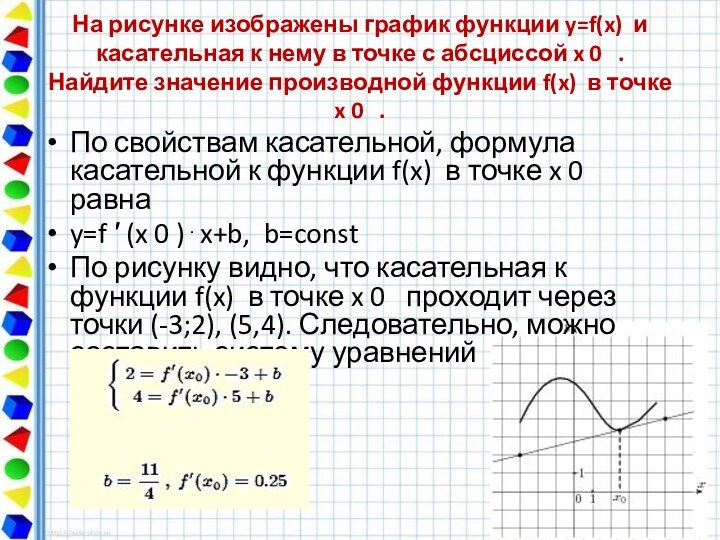
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 8). Найдите количество точек максимума функции f(x) на отрезке [−9;6].

интервале (−1; 12). Определите количество целых точек, в которых

Производная функции отрицательна на тех интервалах, на которых функция убывает, т. е. на интервалах (0,5; 3), (6; 10) и (11; 12). В них содержатся целые точки 1, 2, 7, 8 и 9. Всего 5 точек. Ответ: 5.

на интервале (−10; 4). Найдите промежутки убывания функции f(x).

Решение. Промежутки убывания функции f(x) соответствуют промежуткам, на которых производная функции отрицательна, то есть интервалу (−9; −6) длиной 3 и интервалу (−2; 3) длиной 5. Длина наибольшего из них равна 5. Ответ: 5.

на интервале (−7; 14). Найдите количество точек максимума функции f(x)

Решение. Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [−6; 9] функция имеет одну точку максимума x = 7. Ответ: 1.

на интервале (−8; 6). Найдите промежутки возрастания функции f(x).

Решение. Промежутки возрастания функции f(x) соответствуют промежуткам, на которых производная функции положительна, то есть интервалам (−7; −5), (2; 5). Наибольший из них — интервал (2; 5), длина которого 3.

на интервале (−7; 10). Найдите количество точек минимума функции f(x)

Решение. Точки минимума соответствуют точкам смены знака производной с минуса на плюс. На отрезке [−3; 8] функция имеет одну точку минимума x = 4. Ответ: 1.

на интервале (−16; 4). Найдите количество точек экстремума функции f(x)

Решение. Точки экстремума соответствуют точкам смены знака производной — изображенным на графике нулям производной. Производная обращается в нуль в точках −13, −11, −9, −7. На отрезке [−14; 2] функция имеет 4 точки экстремума. Ответ: 4.

интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
Решение. Заданная

к нему в точке с абсциссой x0. Найдите значение

Решение. Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB

и касательная к этому графику в точке абсциссой, равной

Для решения используем геометрический смысл производной: значение производной функции в точке равняется угловому коэффициенту касательной к графику этой функции, проведенной в этой точке. Угловой коэффициент касательной равен тангенсу угла между касательной и положительным направлением оси х (tg α). Угол α = β, как накрест лежащие углы при параллельных прямых y=0, y=1 и секущей-касательной. Для треугольника ABC

к нему в точке с абсциссой x 0   . Найдите

По свойствам касательной, формула касательной к функции f(x)  в точке x 0   равна
y=f ′ (x 0 )⋅x+b,  b=const 
По рисунку видно, что касательная к функции f(x)  в точке x 0   проходит через точки (-3;2), (5,4). Следовательно, можно составить систему уравнений