- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сечение пирамиды
Содержание
- 2. ИсторияНачало геометрии пирамиды было положено в Древнем
- 3. УчёныеПервый, кто установил, чему равен объем пирамиды,
- 4. Значение в математике Пирамидой называется многогранник,
- 5. ФормулыОбъём пирамиды может быть вычислен по формуле:
- 6. Применение в жизниПирамида — вид архитектурного сооружения в
- 7. Пирамида в архитектуреПирамида в спортеВ экономике
- 8. Решение задачВ разделе “Свойства сечения пирамиды плоскостью,параллельной
- 9. Рассмотрим каждую теоремуТеорема1.Сечение пирамиды плоскостью,параллельной основанию, является
- 10. Теорема2.Отношение площади основания пирамиды к площади её
- 11. задачаВсе боковые ребра пирамиды равны между
- 12. Скачать презентацию
- 13. Похожие презентации
ИсторияНачало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции.











Слайд 3
Учёные
Первый, кто установил, чему равен объем пирамиды, был
Демокрит, а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал
знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.
Слайд 4
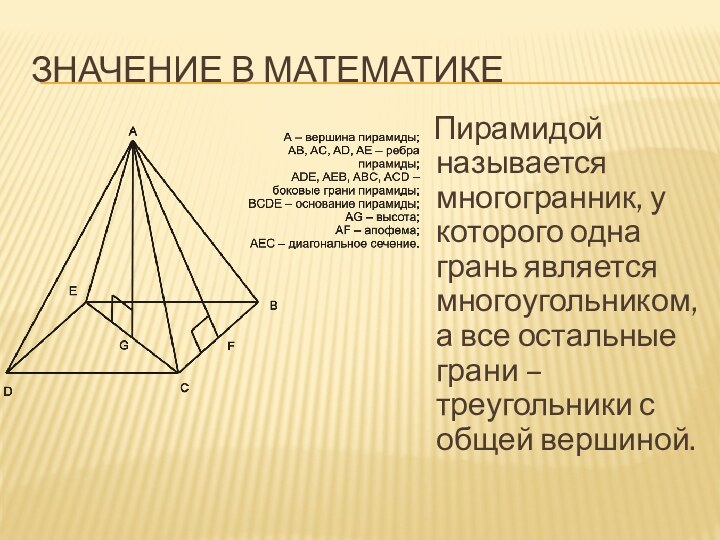
Значение в математике
Пирамидой называется многогранник, у
которого одна грань является многоугольником, а все остальные грани
– треугольники с общей вершиной.
Слайд 5
Формулы
Объём пирамиды может быть вычислен по формуле:
где S — площадь основания и h — высота;
Боковая поверхность — это сумма площадей боковых граней:Полная поверхность — это сумма боковой поверхности и площади основания:
Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
где a — апофема , — P периметр основания, n — число сторон основания, b — боковое ребро, a— плоский угол при вершине пирамиды.
Слайд 6
Применение в жизни
Пирамида — вид архитектурного сооружения в форме
пирамиды.
Финансовая пирамида — способ получения дохода за счёт постоянного расширяющегося
привлечения денежных средств от новых участников.Пирамида — элемент художественной, силовой и пластической акробатики, групповое расположение акробатов, которые, поддерживая друг друга, образуют сложные фигуры.
Слайд 8
Решение задач
В разделе “Свойства сечения пирамиды плоскостью,параллельной основанию
“ придлогается для рассмотрения 2 теоремы .
Теорема1.Сечение пирамиды плоскостью,параллельной
основанию, является многоугольником, подобным основанию.Теорема2.Отношение площади основания пирамиды к площади её параллельного основанию сечения равно отношению квадратов высот соответствующих пирамид.
Слайд 9
Рассмотрим каждую теорему
Теорема1.Сечение пирамиды плоскостью,параллельной основанию, является многоугольником,
подобным основанию.
Доказательство.
Два многоугольника подобны, если их соответственные стороны пропорциональны
и соответственные углы равны. Углы рассматриваемых многоугольников, вершины которых расположены на одном и том же ребре, равны, так как их стороны параллельны и одинаково направлены.Согласно теореме Фалеса параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки .Поэтому A1SB1~ASB,B1SC1 ~ BSC и, следовательно , A1B1/AB = SB1/SB и B1C1/BC = SB1/SB ,откуда A1B1/AB = B1C1/BC Последнее равенство означает ,что для одной пары соответственных и равных углов прилежащие к ним соответственные стороны многоугольников пропорциональны .Аналогично доказательству равенство всех остальных соответственных углов и пропорциональность соответственных сторон: A1B1/AB = B1C1/BC = C1D1/CD= D1E1/DE= E1A1/EA
Слайд 10 Теорема2.Отношение площади основания пирамиды к площади её параллельного
основанию сечения равно отношению квадратов высот соответствующих пирамид.
Доказательство. Проведём
к призме высоту SO и пусть O1 -основание высоты пирамиды, отсекаемой от исходной пирамиды данным сечением. Обозначим через Sосн площадь исходной пирамиды и через Sс-площадь сечения .Треугольники SB1O1 и SBO подобны (почему?) и поэтому SB1/SB= SO1/SO . При доказательстве предыдущей теоремы мы убедились в том , что SB1/SB = A1B1/AB и поэтому SO1/SO= A1B1/AB ..Как мы знаем , площади подобных многоугольников относиться как квадраты их соответственных сторон . Следовательно ,Sсеч/Sосн = A1B1²/AB²,или Sсеч/Sосн = SO1²/SO²
Слайд 11
задача
Все боковые ребра пирамиды равны между собой
.Какие фигуры могут лежать в основании этой пирамиды
?Прямоугольник
Ромб
Треугольник
Параллелограмм
Прямоугольная трапеция