- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника
Содержание
- 2. Цель урока: Ознакомление с понятием симметрии в
- 6. Их изучали ученые, ювелиры, священники, архитекторы. Этим
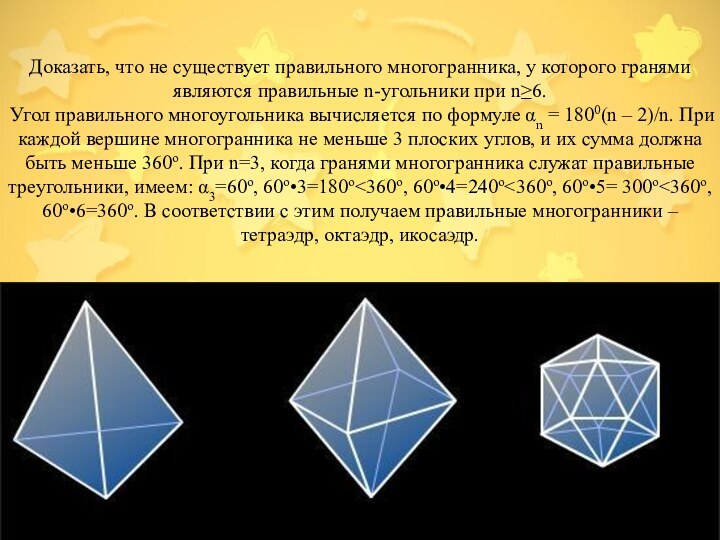
- 7. Доказать, что не существует правильного многогранника, у
- 8. Если n=4, то есть грани многогранника – квадраты, α4=90о, 90о•3=270о
- 9. Если n=5, то есть грани многогранника –
- 10. Правильный тетраэдр не имеет центра симметрии. Прямая,
- 11. Куб имеет один центр симметрии —
- 12. Правильный октаэдр, правильный икосаэдр и правильный
- 13. Решить задачи №276, 277, 278 (устно); №281, 282, 287.
- 14. Домашнее задание: п. 31 – 33,
- 15. Скачать презентацию
- 16. Похожие презентации
Цель урока: Ознакомление с понятием симметрии в пространстве и с понятием правильного многогранникаЗадачи урока: Ввести понятие правильного многогранника, рассмотреть все пять видов правильных многогранников