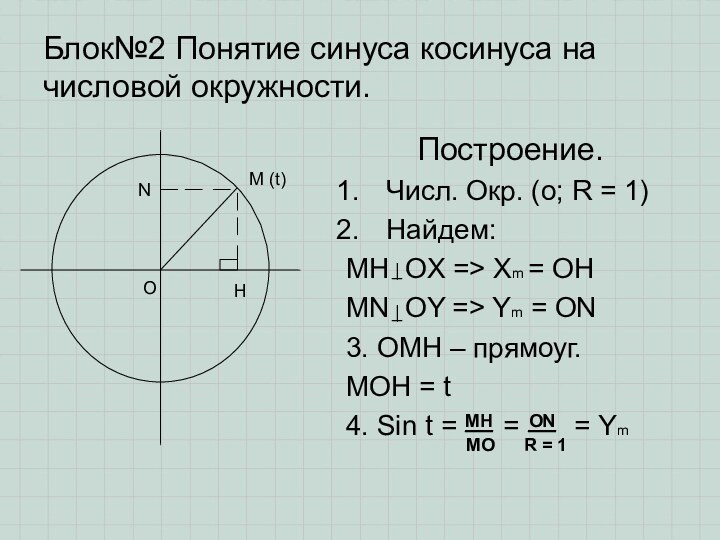
Построение.
ABC – прямоуг.
А = – острый
Найдем: sin
=cos =
tg =
ctg =
А
С
В
CB
AB
AC
AB
AC
CB
AC
CB
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



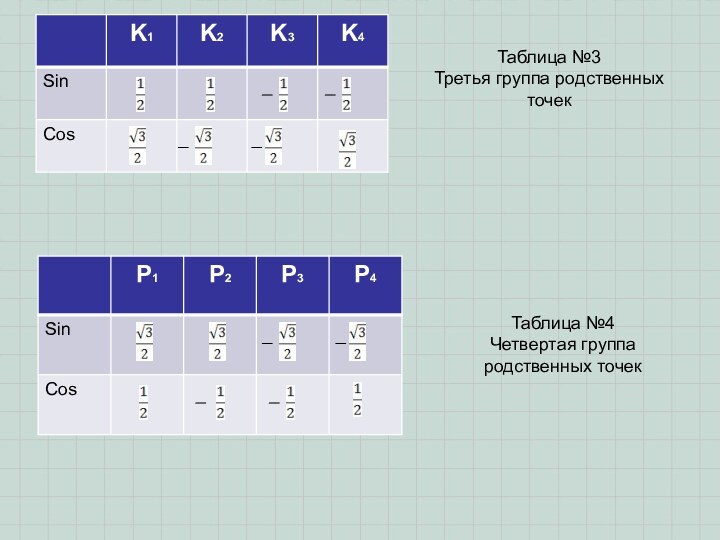






А
С
В
CB
AB
AC
AB
AC
CB
AC
CB
О
Н
М (t)
N
_
|
|
_
MH
MO
ON
R = 1
OH
OM
ym
R=1
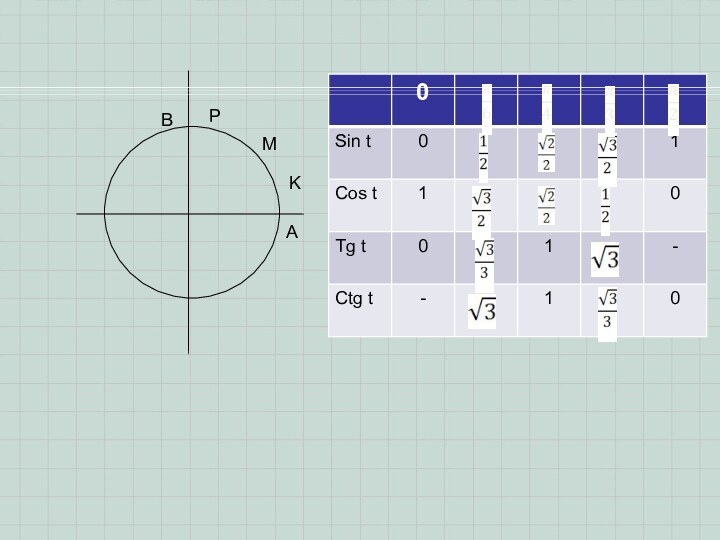
Sin t = Ym
Cos t = Xm
.
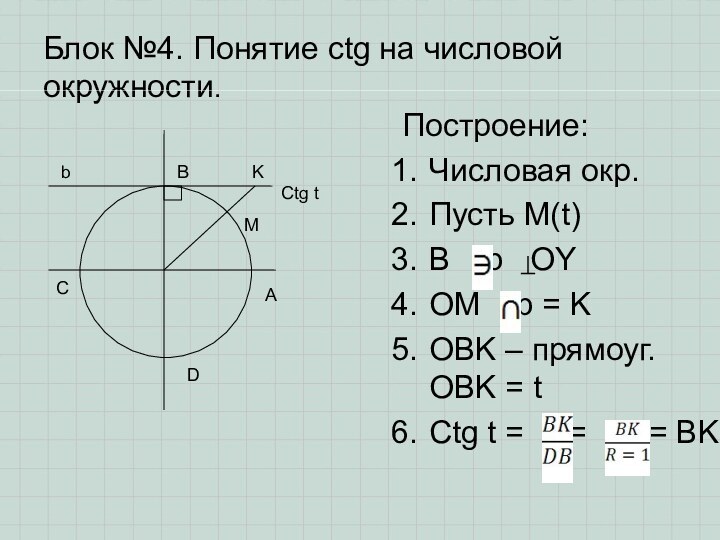
N
M
A
K
Tg t
Tg t1
L1
O
A
B
C
D
M
K
Ctg t
b