- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сказка о стране чисел
Содержание
- 2. Цель работы: Создать электронную версию сказки
- 3. Сказка о стране чиселСказка о Стране Чисел
- 4. Давным-давно, в глубокой древности, на бескрайних просторах Камчатки, жили-поживали натуральные числа.
- 5. Они помогали людям выполнить арифметические действия: сложение,
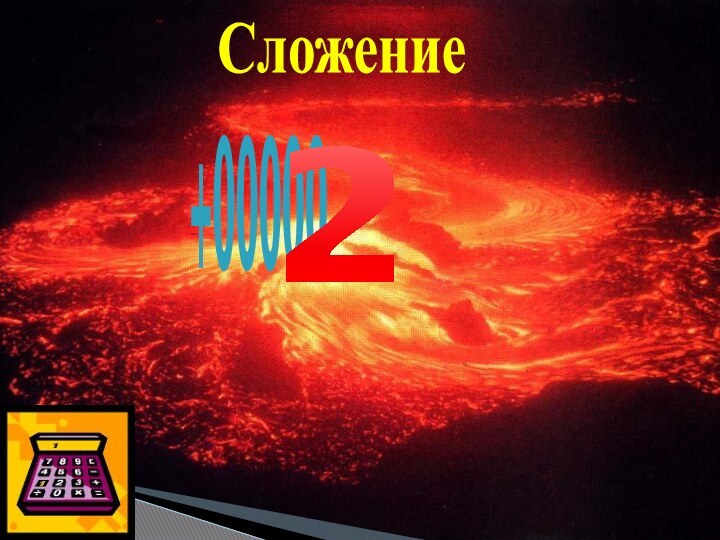
- 6. Сложение2+000002=4
- 7. Вычитание6-2=?4
- 8. Умножение 2 · 4=88:2=4и деление
- 9. Возведение в степень 23=2x2x2=8
- 10. Извлечение корня =4=1=2=3=5
- 11. Правда, вычитание, деление и извлечение корня не
- 12. Однажды в страну Чисел пришёл незнакомец Координатный
- 13. Натуральные числа решили последовать совету незнакомца,
- 14. Ах как заважничала Единица! Она стала толстая
- 15. Разрабатывая земельные участки между своими
- 16. В стране чисел праздник. На почётном месте
- 17. 1,250,81,20,83333…
- 18. Наступает тишина… У десятичной дроби появляется бесконечный
- 19. На помощь приходит грозный Период. Он быстро
- 20. Вычитание по прежнему доставляет числам беспокойство. Ну
- 21. Правда, удаляется эта улица от ноля влево,
- 22. Теперь из числа 3 легко вычесть число 5, получается число -2. Проблема вычитания решена. Ура! 3-5=-2
- 23. Страна чисел с появлением дробных и отрицательных
- 24. На этом развитие страны чисел не закончилось.
- 25. Скачать презентацию
- 26. Похожие презентации
Цель работы: Создать электронную версию сказки о стране чисел Задачи:Составить наглядное представление о числах и действиях над ними.Развить интерес младших школьников к математике.






















Слайд 2 Цель работы: Создать электронную версию сказки о стране
чисел
интерес младших школьников к математике.
Слайд 3
Сказка о стране чисел
Сказка о Стране Чисел дает
возможность пройти путь развития понятия числа чуть дальше, чем
это происходит в школе и оставляет простор для творчества.Слайд 4 Давным-давно, в глубокой древности, на бескрайних просторах Камчатки, жили-поживали
натуральные числа.
Слайд 5 Они помогали людям выполнить арифметические действия: сложение, вычитание,
умножение, деление и даже более сложные – возведение в
степень и извлечение корня.Слайд 11 Правда, вычитание, деление и извлечение корня не всегда
выполнялось: результат не попадал в множество натуральных чисел. Числа
много и честно трудились, в любую минуту приходя на помощь людям, но очень страдали от того, что не всё у них получалось...Слайд 12 Однажды в страну Чисел пришёл незнакомец Координатный Луч.
Он предложил всем натуральным числам поселиться на одной длинной-предлинной
улице, у которой есть начало, но нет конца.Слайд 13 Натуральные числа решили последовать совету незнакомца, но
ни кто из них не хотел жить на окраине.
Тогда Единица предложила слева от себя построить всем миром дом для маленькой невзрачной цифры ноль. Все дружно согласились. Ноль хоть и не натуральное число, а только цифра, очень не обходим для 10, 305, 1000000 и т.д.Слайд 14 Ах как заважничала Единица! Она стала толстая и
внушительная, построила себе самый красивый и большой дом. Расстояние
от скромного жилища нолика до этого огромного дома назвали Единичным Отрезком.1
2
3
Единичный отрезок
Все остальные натуральные числа сделали расстояние между своими домами, таким же, как единичный отрезок.
Един
0
Слайд 15 Разрабатывая земельные участки между своими домиками,
они обнаружили там дроби. Интересный вид у этих новых
жителей Страны чисел. Казалось бы два обычных натуральных числа, но между ними перекладина, дробная черта. Знаменатель дроби, тот что внизу, держит над собой эту перекладину, а числитель, как акробат, балансирует на ней , например:
Слайд 16
В стране чисел праздник.
На почётном месте дробная
черта
и знак деления. Они с огромным интересом смотрят,
как
натуральные числа,
разбившись на пары,
составляют дроби,
выполняют деление
числителя на знаменатель,-- и дробь из
обыкновенной
превращается
в десятичную.
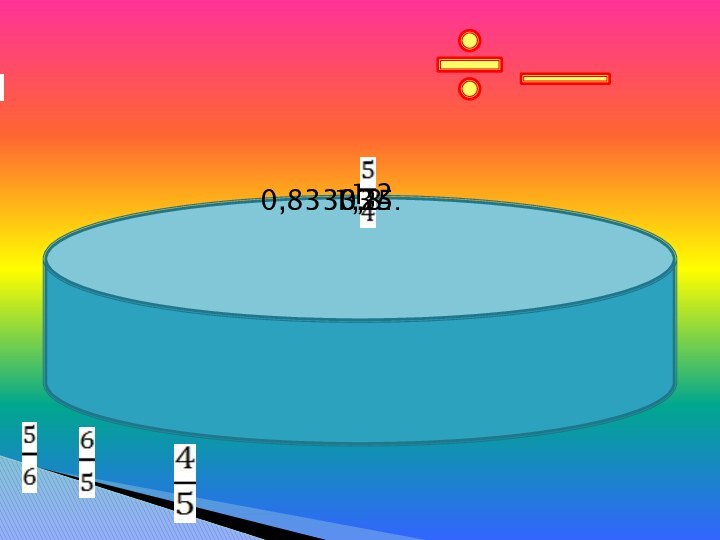
Слайд 18 Наступает тишина… У десятичной дроби появляется бесконечный «хвост»
из Повторяющейся цифры 3 (0.833333…). Оглянувшись вокруг, числа замечают,
«хвостатых» дробей очень много:Что делать?
Слайд 19 На помощь приходит грозный Период. Он быстро отрубает
«хвосты», заковывает повторяющуюся цифру или группу цифр в круглые
скобки. Получаются аккуратненькие бесконечные периодические дроби.ПЕРИОД
0,8333…
0,181818
0,8(3)
0,(18)
Слайд 20 Вычитание по прежнему доставляет числам беспокойство. Ну что
делать, когда надо из 3 вычесть5? Не получается натуральное
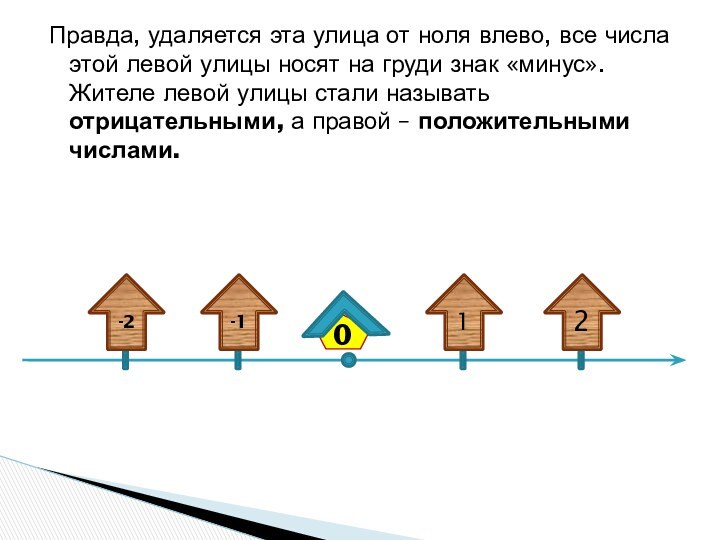
число. На помощь пришёл ноль. Он уже подрос, перестал быть ноликом - хулиганчиком, когда то укравшим со склада знак умножения. Теперь ноль стал умным, начитанным, думающим юношей. Он исследовал территорию около своего скромного жилища и сделал величайшее открытие: слева от него тоже есть числа! Они очень похожи на натуральные и дробные, живут на такой же бесконечной улице.Слайд 21 Правда, удаляется эта улица от ноля влево, все
числа этой левой улицы носят на груди знак «минус».
Жителе левой улицы стали называть отрицательными, а правой – положительными числами.Един
0
-2
-1
1
2