Презентация на тему Тригонометрические функции любого угла

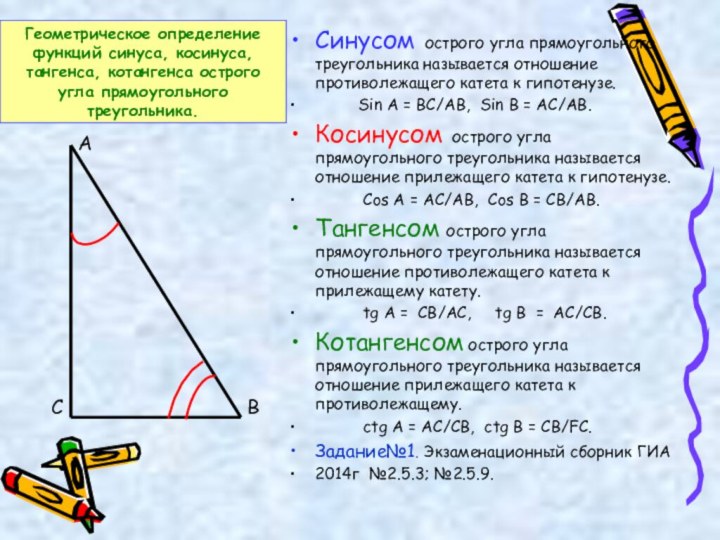
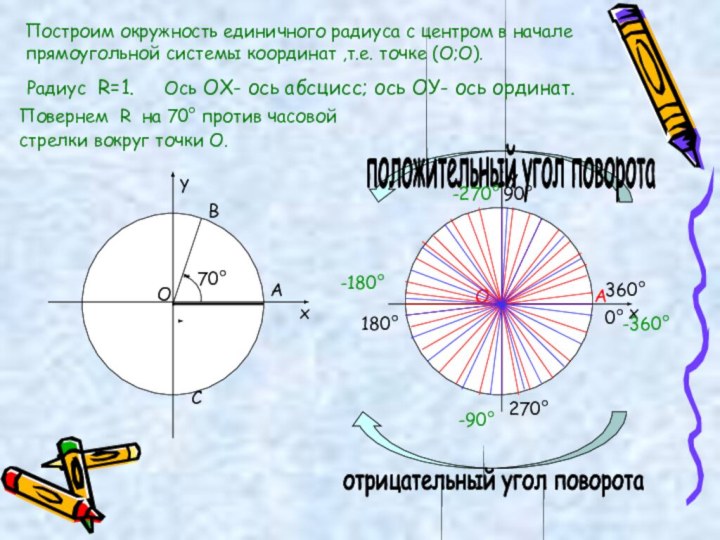
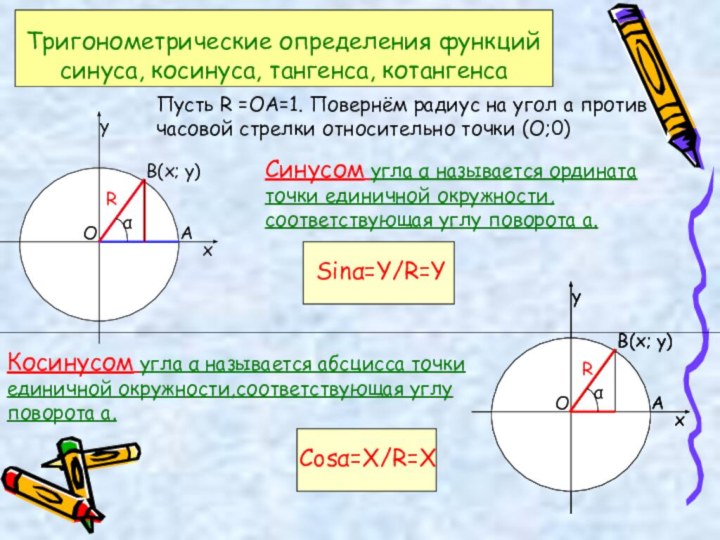
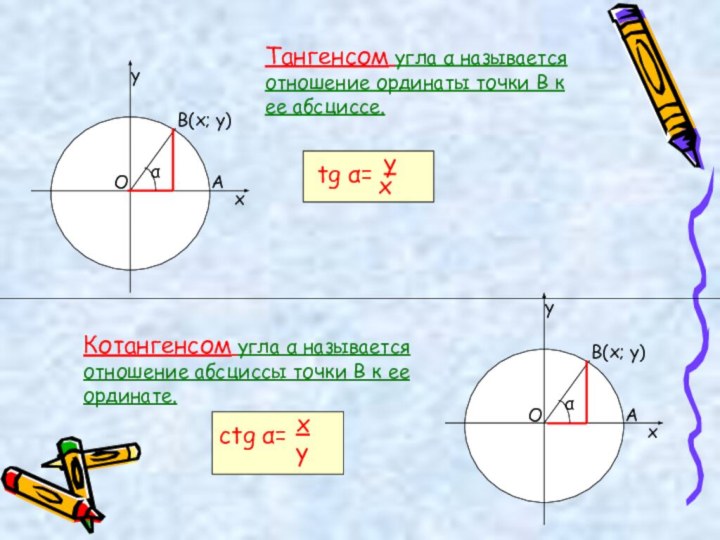
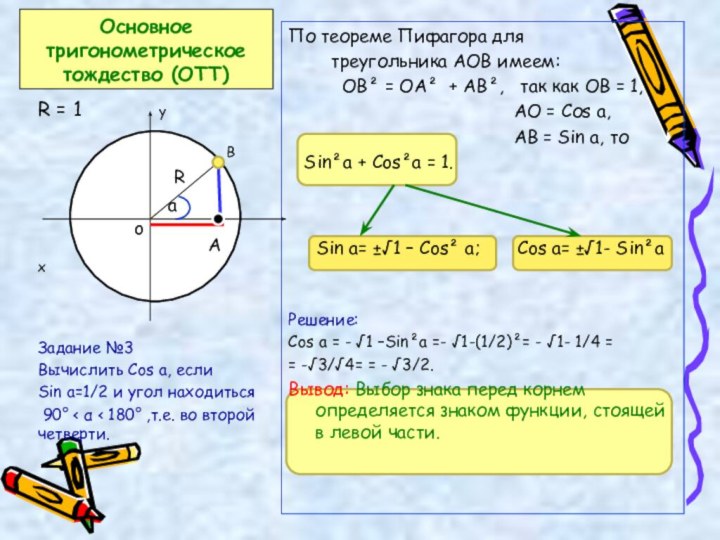
урока: комбинированный урок, т.е. изучения нового материала и формирование

умений на базе нового материала.

Метод :диалогическое изложение материала с использованием ИТ, с репродуктивным решением стереотипных задач.

Структура урока:

1.Актуализация знаний.
2.Формирование новых понятий и способов действий.
3.Формирование умений и навыков.

Виды деятельности: групповая, индивидуальная ( учитывая особенности класса).

угла прямоугольного треугольника.
Синусом острого угла прямоугольного треугольника называется отношение

противолежащего катета к гипотенузе.
Sin A = BC/AB, Sin B = AC/AB.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Cos A = AC/AB, Cos B = CB/AB.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
tg A = CB/AC, tg B = AC/CB.
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
ctg A = AC/CB, ctg B = CB/FC.
Задание№1. Экзаменационный сборник ГИА
2014г №2.5.3; №2.5.9.

А












С В

М перемещается по лучу ОN, занимая последовательно положения М(Х,У)

и
М1(Х 1; У1). Треугольники МХО и М1Х1О - подобны по теореме Фалеса, следовательно их сходственные стороны пропорциональны.
У/ОМ = У1/ОМ1 = Sin (NOX)
Х/ОМ = Х1/ОМ1 = Cox (NOX)
У/Х = У1 /Х1 = tg (NOX)
Х/У = Х1 /У1 = ctg (NOX)
Рассматриваемые отношения не зависят от
расстояния точки М до начала координат,
а зависят только от величины угла
поворота NОX.
Существует однозначное соответствие между углами поворота луча ОN и величинами приведённых отношений.
Вывод: Эти отношения можно считать функциями угла поворота NОX и их называют тригонометрическими функциями, а расстояние точки М от начала координат можно принять равным «1».

Y
N


M1(X1;Y1 )

M(X;Y)


Y Y1


O X X1 X

прямоугольной системы координат ,т.е. точке (О;О).
Радиус R=1.

Ось ОХ- ось абсцисс; ось ОУ- ось ординат.

Повернем R на 70° против часовой стрелки вокруг точки О.

А

О

ОА повернуть на 180° ,
180°
а потом еще

на 30°,

то угол поворота будет равен 210°.

210°

Если начальный радиус ОА сделает полный оборот против часовой стрелки, то угол поворота будет равен 360° .
Если начальный радиус сделает полный оборот по часовой стрелке, то угол поворота будет равен
(- 360°).

360°

Вывод: угол поворота может выражаться каким угодно числом градусов от -∞ до + ∞.

α ‹ 90°, то угол в I четверти;

- если

90° ‹ α ‹ 180°, то угол во II четверти;

-если 180° ‹ α ‹ 270°, то угол в III четверти;

-если 270° ‹ α ‹ 360°, то угол в IV четверти.

Задание №2. В какой четверти находиться угол 420°? Чему равен синус этого угла?

т.к. 420°= 360°+60° и 0 °‹ 60°‹ 90°, то этот угол лежит в I четверти.
Пользуясь таблицей значений тригонометрических функций, находим: синус 60°равен √3/2.

Углы 0°, ±90°, ±180°, ±270°, ±360° не относятся ни к какой четверти.

А

О

В

a против часовой стрелки относительно точки (О;0)

Синусом угла

α называется ордината точки единичной окружности, соответствующая углу поворота a.

R

Косинусом угла α называется абсциссa точки единичной окружности,соответствующая углу поворота a.

R

R

Тригонометрические определения функций синуса, косинуса, тангенса, котангенса

к ее абсциссе.
Котангенсом угла α называется отношение абсциссы

точки В к ее ординате.

треугольника АОВ имеем:

OB² = ОА² + АB², так как ОВ = 1,
АО = Соs a,
AB = Sin a, то
Sin²a + Cos²a = 1.

Sin a= ±√1 – Cos² a; Cos a= ±√1- Sin²a


Решение:
Cos a = - √1 –Sin²a =- √1-(1/2)²= - √1- 1/4 =
= -√3/√4= = - √3/2.
Вывод: Выбор знака перед корнем определяется знаком функции, стоящей в левой части.

R = 1 у

В



а
0) х А x



Задание №3
Вычислить Cos a, если
Sin a=1/2 и угол находиться
90° < α < 180° ,т.е. во второй четверти.

o

R

a

А