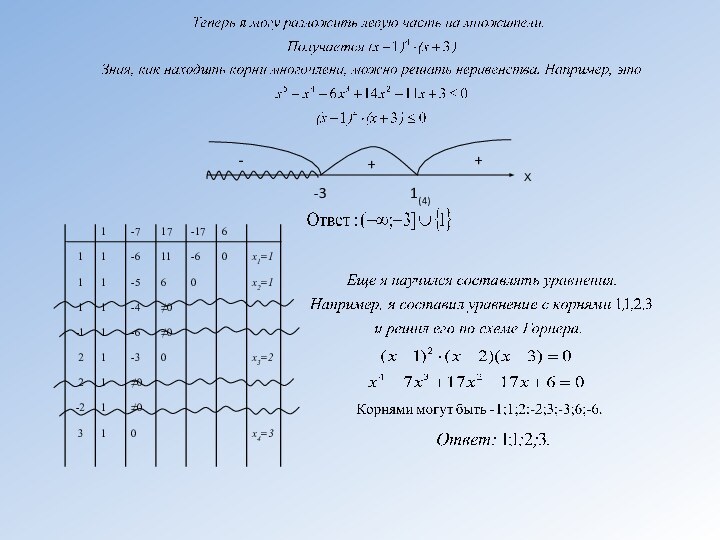
Деление многочленов с остатком;
Решение алгебраических уравнений 3-й и 4-й
степени;Симметрические и возвратные уравнения;
формулы Виета, Горнера и Безу.
Применить полученные знания при решении задач группы С, а именно С5.