методам систематизации, обработки и использования статистических данных для научных
и практических выводовА.Н. Колмогорови Ю.В. Прохоров
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
























































![Статистические методы обработки экспериментальных данных Новиков Д.А. Статистические методы в педагогических исследованиях (типовые случаи) [Электронный ресурс] :](/img/tmb/14/1397521/9b879a47f18c6be2dc144ee4659f26c5-720x.jpg)
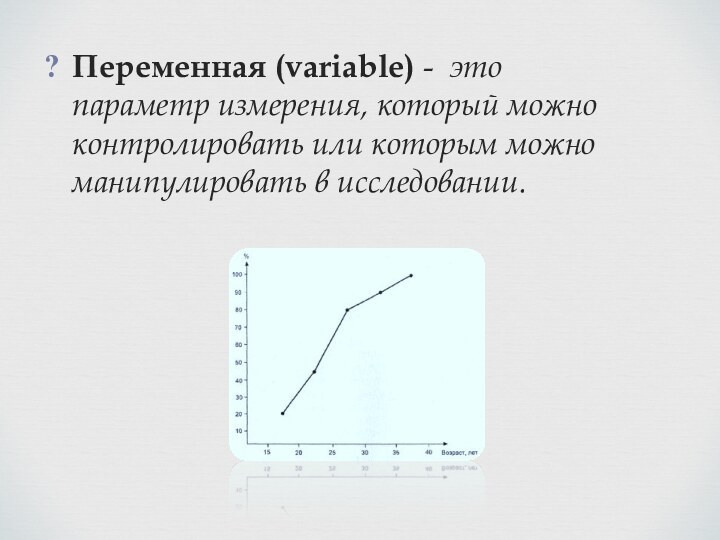
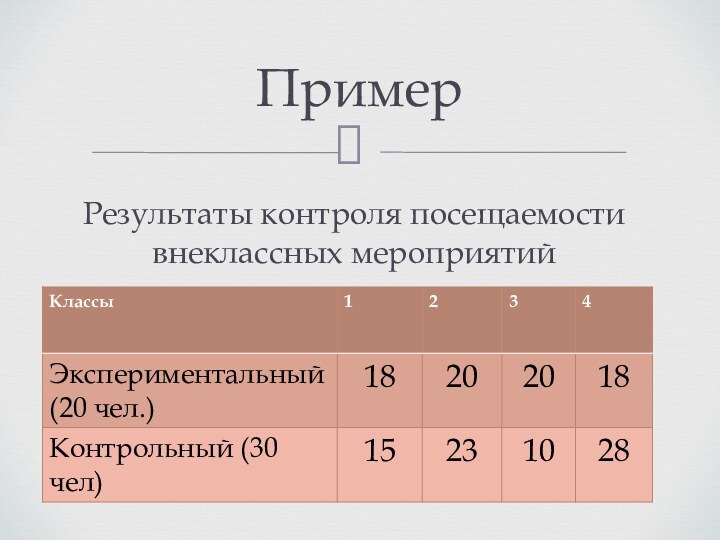
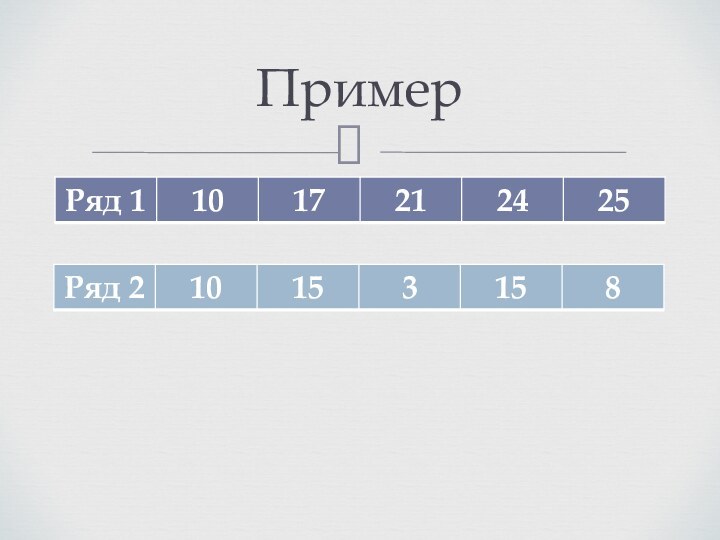
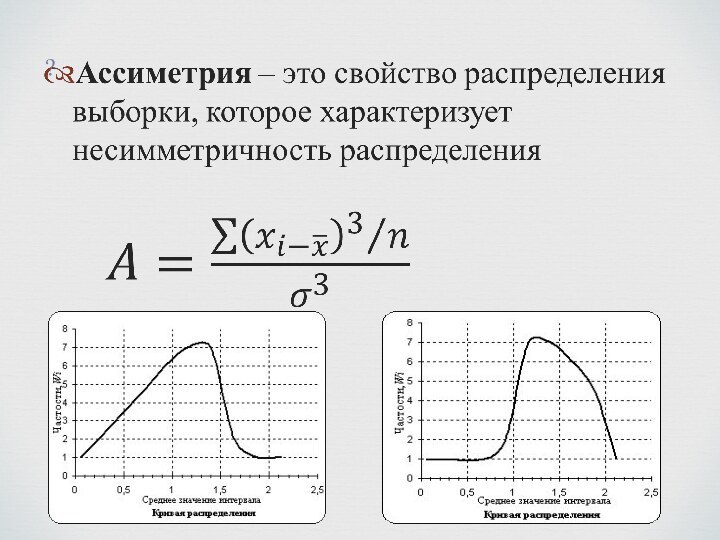
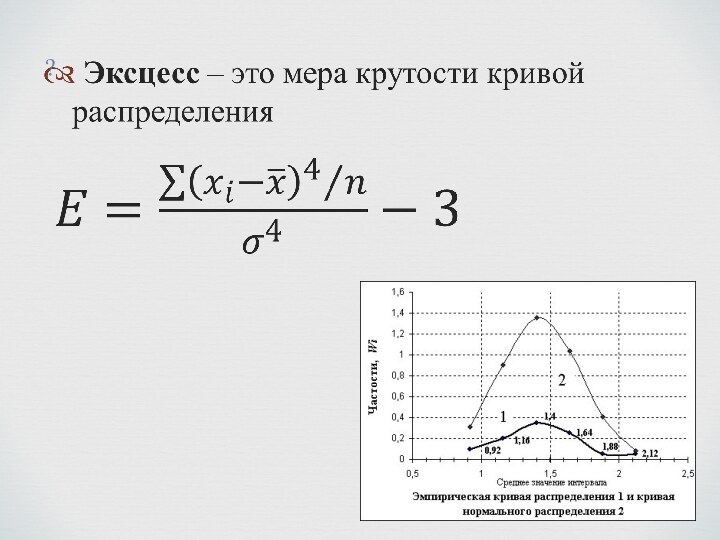
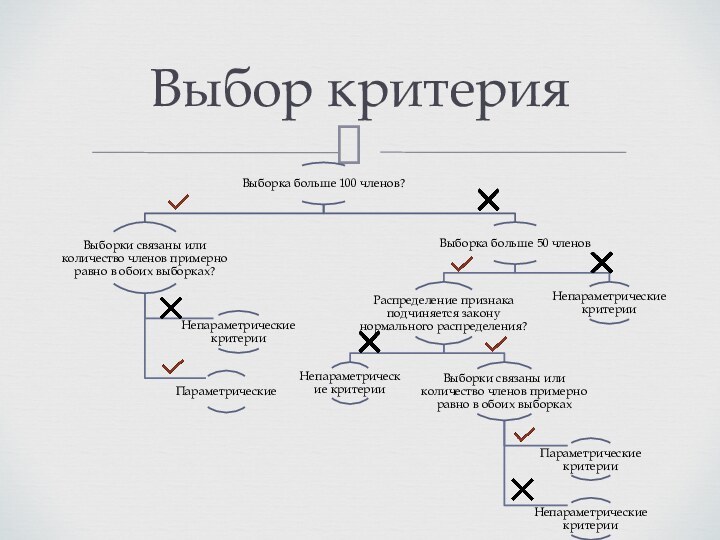
Генеральная и выборочная совокупности
Ошибки при проверке гипотез
Ошибки при проверке гипотез
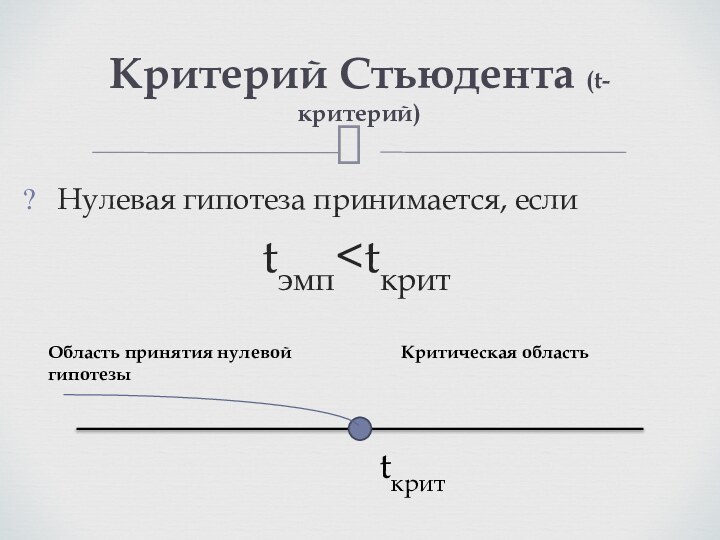
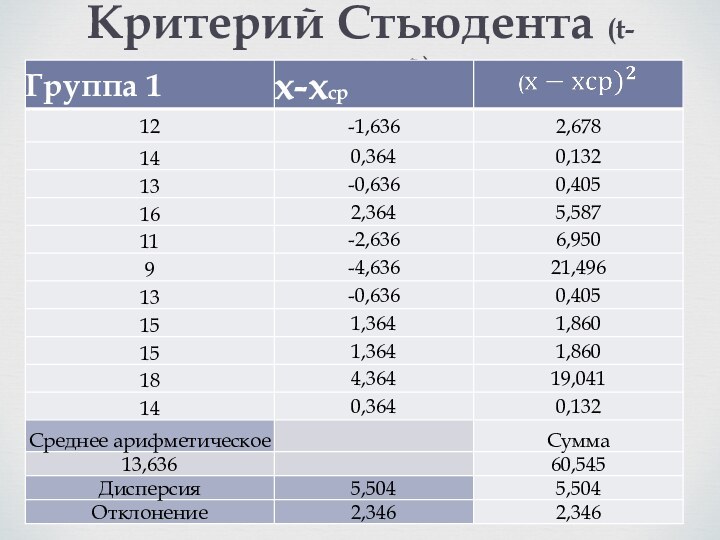
Процедура проверки нулевой гипотезы
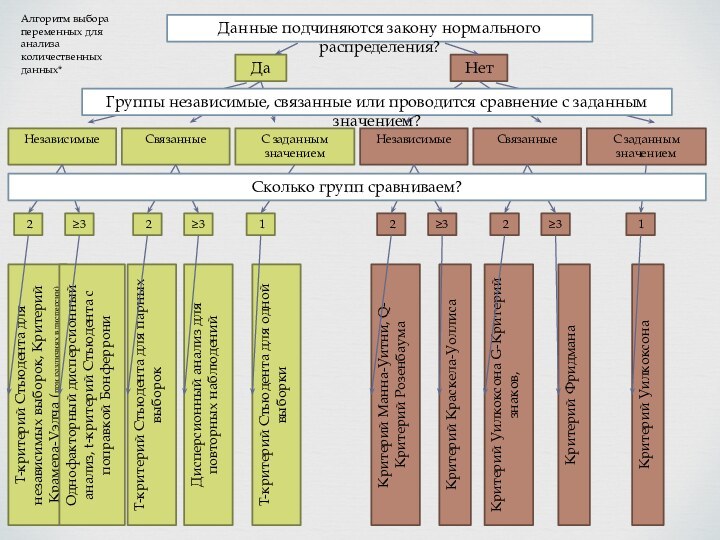
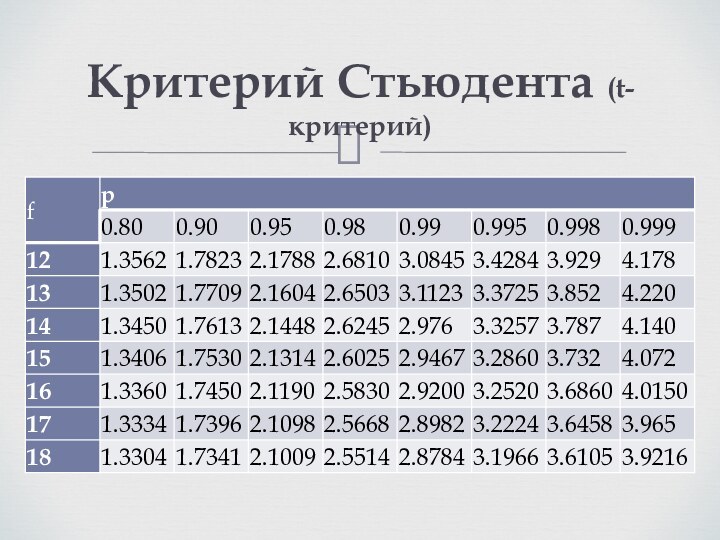
Однофакторный дисперсионный анализ, t-критерий Стьюдента с поправкой Бонферрони
≥3
2
≥3
2
≥3
2
≥3
1
1
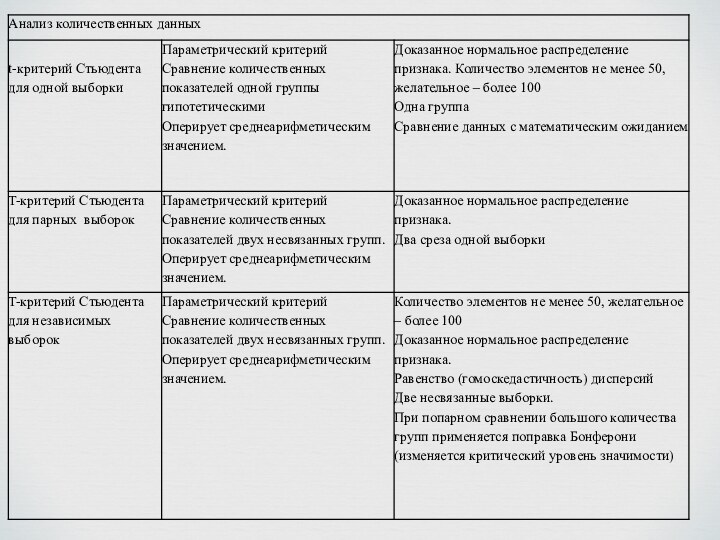
T-критерий Стьюдента для парных выборок
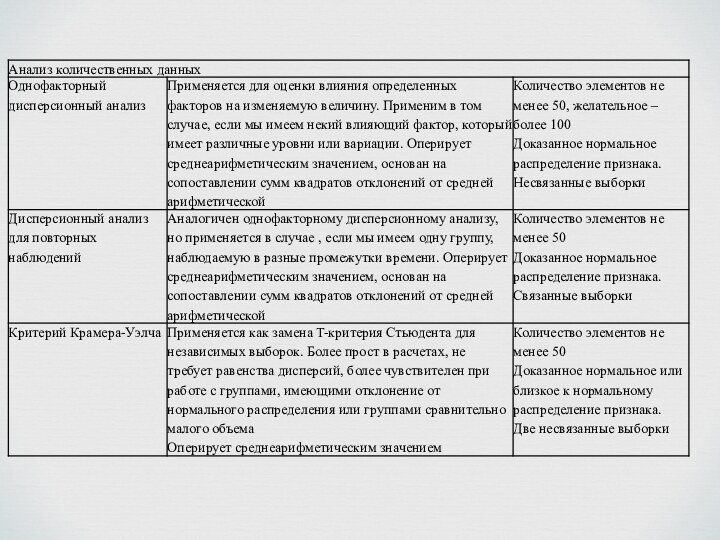
Дисперсионный анализ для повторных наблюдений
T-критерий Стьюдента для одной выборки
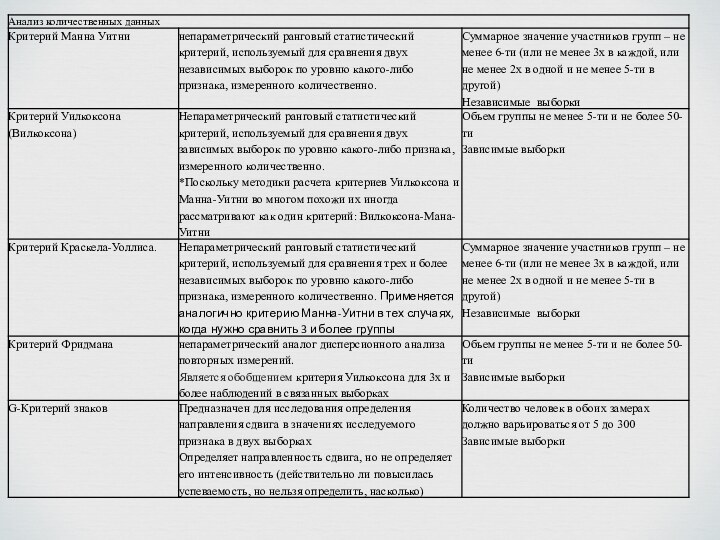
Критерий Манна-Уитни, Q-Критерий Розенбаума
Критерий Краскела-Уоллиса
Критерий Уилкоксона G-Критерий знаков,
Критерий Фридмана
Критерий Уилкоксона
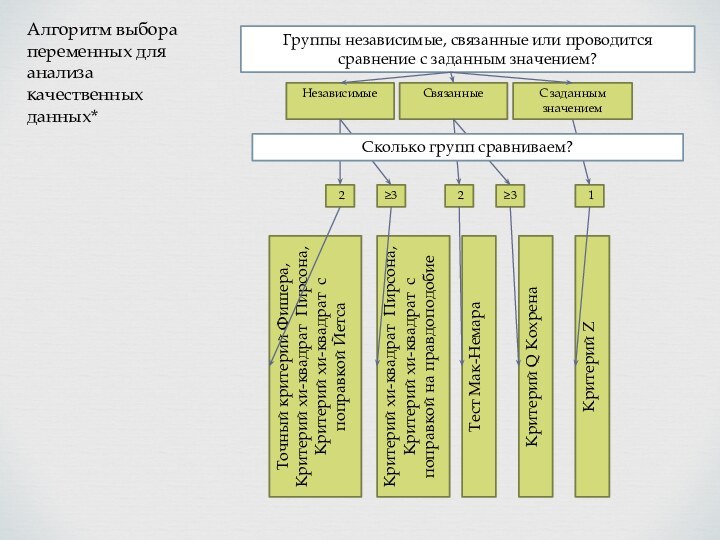
Группы независимые, связанные или проводится сравнение с заданным значением?
Сколько групп сравниваем?
Алгоритм выбора переменных для анализа количественных данных*
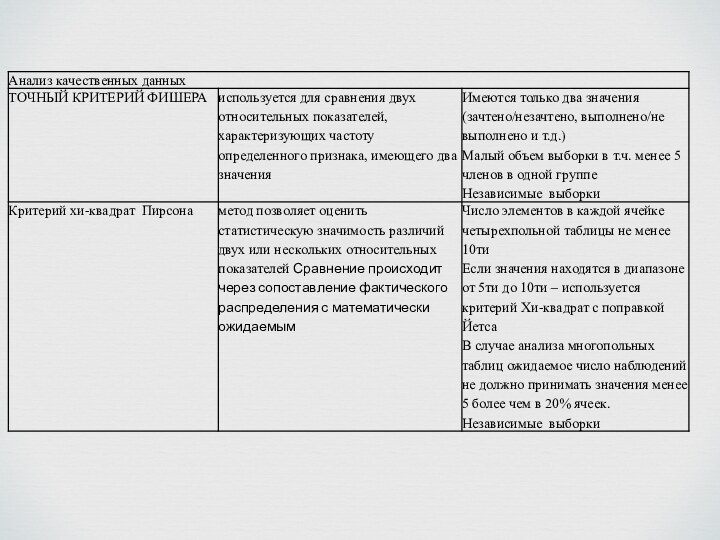
Критерий хи-квадрат Пирсона, Критерий хи-квадрат с поправкой на правдоподобие
≥3
2
≥3
1
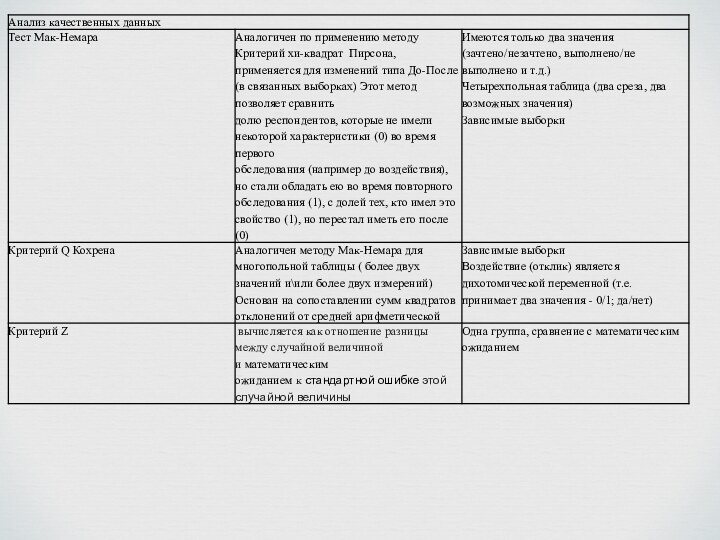
Тест Мак-Немара
Критерий Q Кохрена
Критерий Z
Сколько групп сравниваем?
Алгоритм выбора переменных для анализа качественных данных*
≥3
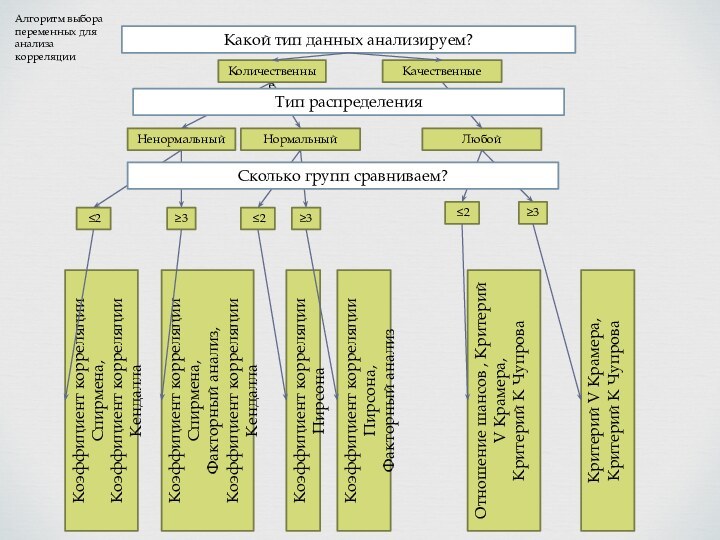
Алгоритм выбора переменных для анализа корреляции
≤2
Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона,
Факторный анализ
≥3
Любой
≤2
Отношение шансов , Критерий V Крамера,
Критерий К Чупрова
Критерий V Крамера,
Критерий К Чупрова
≥3
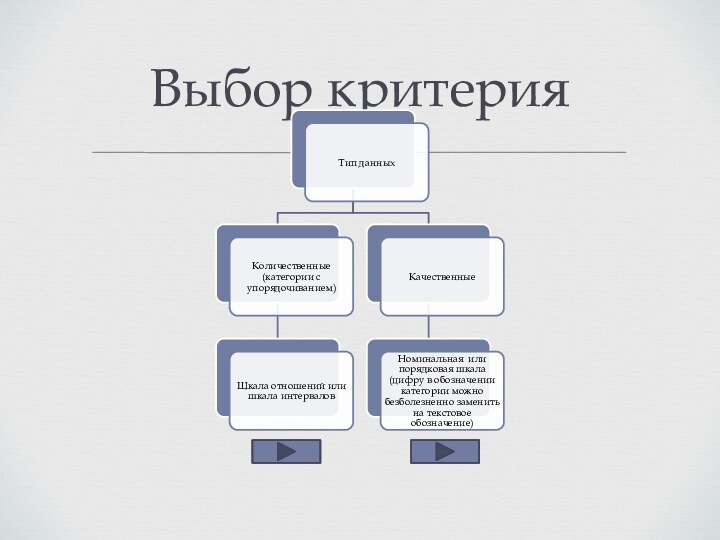
Количественные
Качественные
Тип распределения
Сколько групп сравниваем?
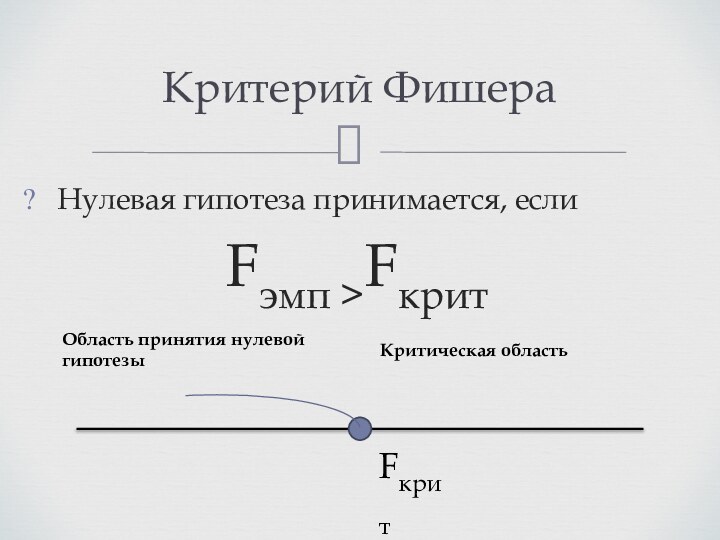
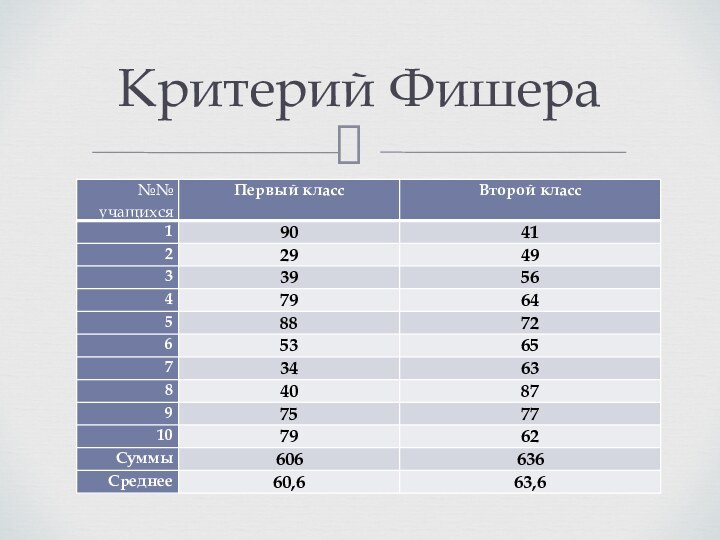
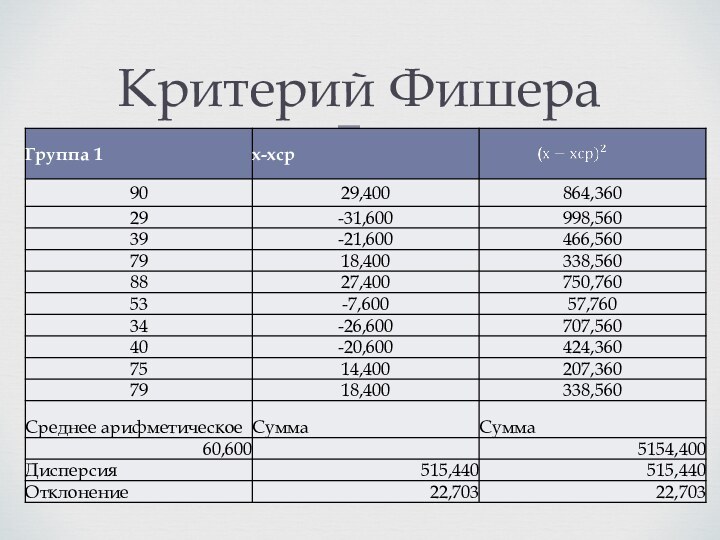
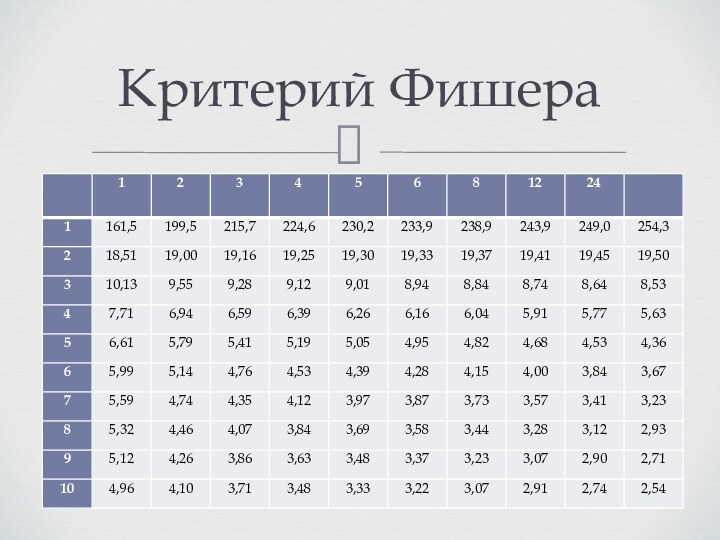
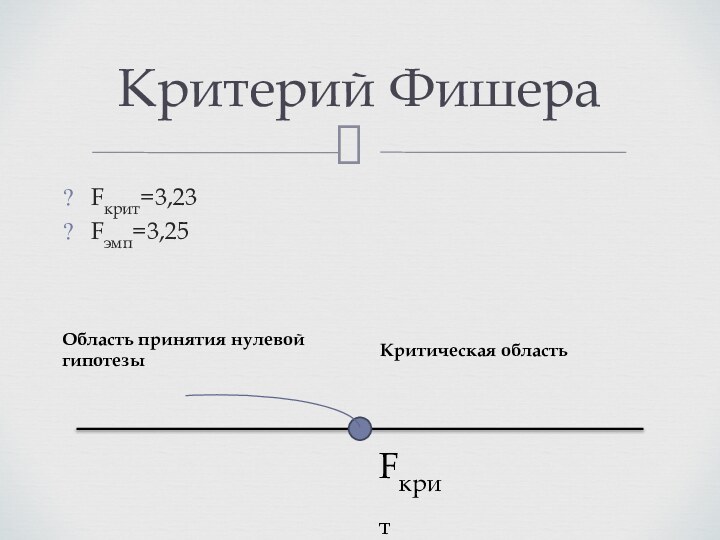
Критерий Фишера
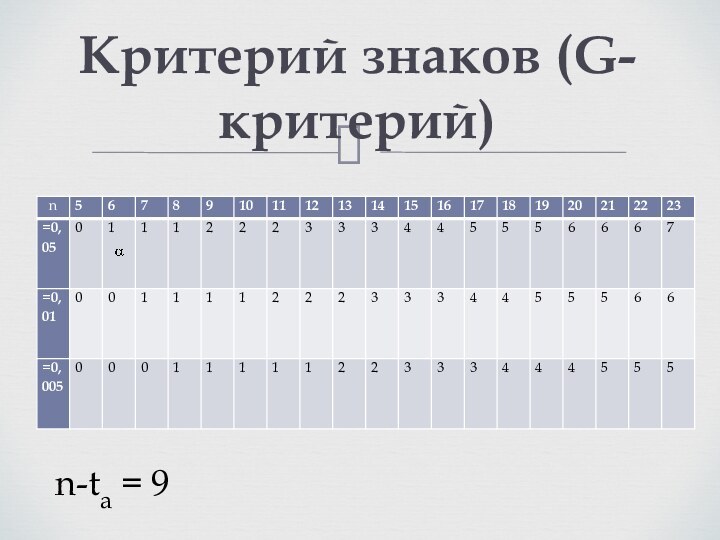
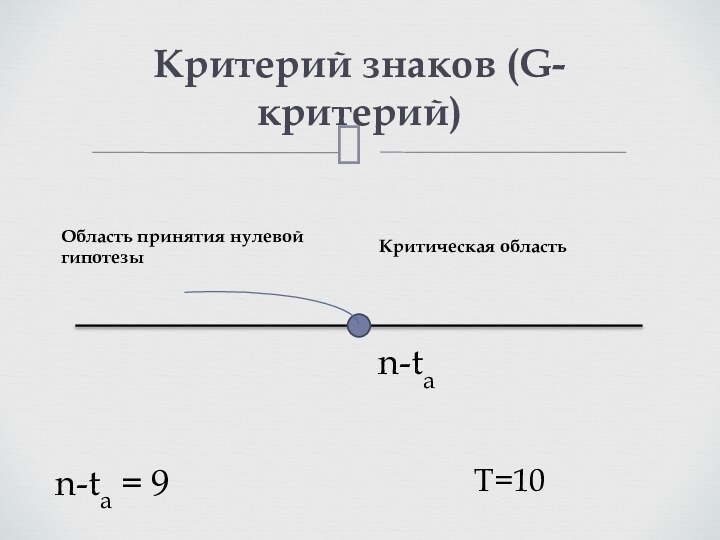
Критерий знаков (G-критерий)
Критерий знаков (G-критерий)
Критерий знаков (G-критерий)
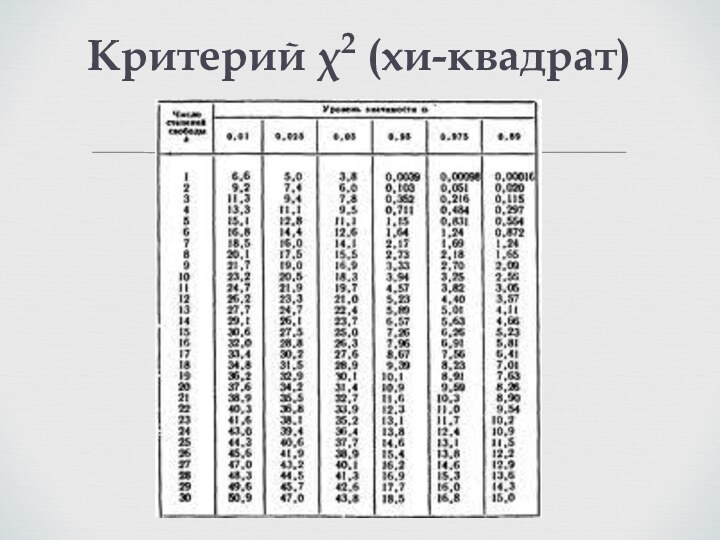
Критерий χ2 (хи-квадрат)