геометрического смысла
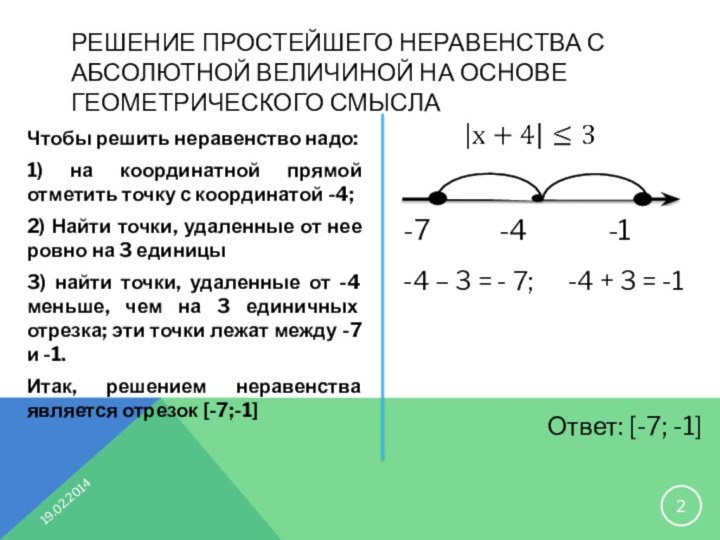
Чтобы решить неравенство надо:
1) на координатной прямой
отметить точку с координатой -4;2) Найти точки, удаленные от нее ровно на 3 единицы
3) найти точки, удаленные от -4 меньше, чем на 3 единичных отрезка; эти точки лежат между -7 и -1.
Итак, решением неравенства является отрезок [-7;-1]
-4 – 3 = - 7; -4 + 3 = -1
Ответ: [-7; -1]