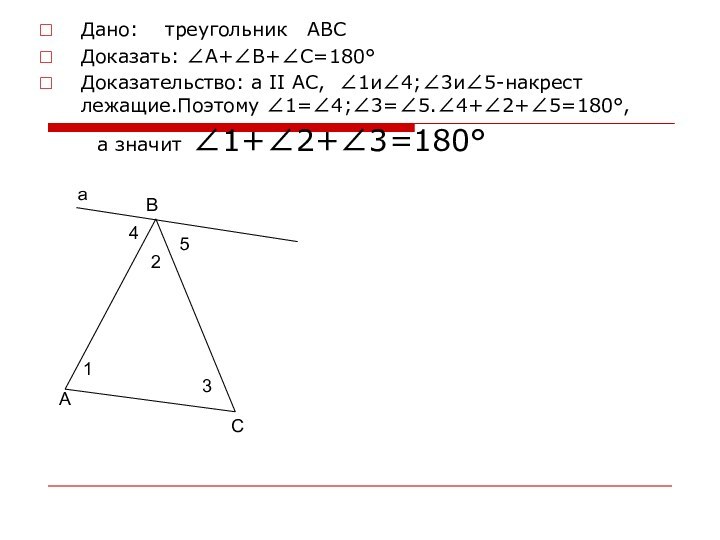
АС, ∠1и∠4;∠3и∠5-накрест лежащие.Поэтому ∠1=∠4;∠3=∠5.∠4+∠2+∠5=180°,
а значит
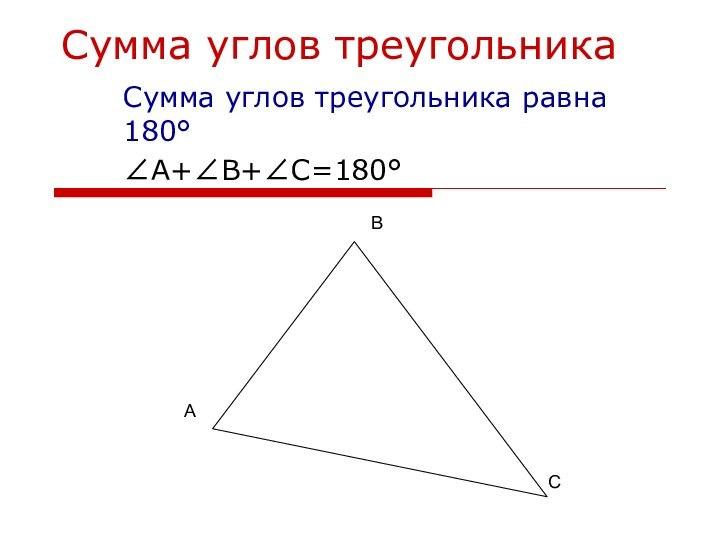
∠1+∠2+∠3=180° А
В
С
а
1
3
2
4
5
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













А
В
С
а
1
3
2
4
5
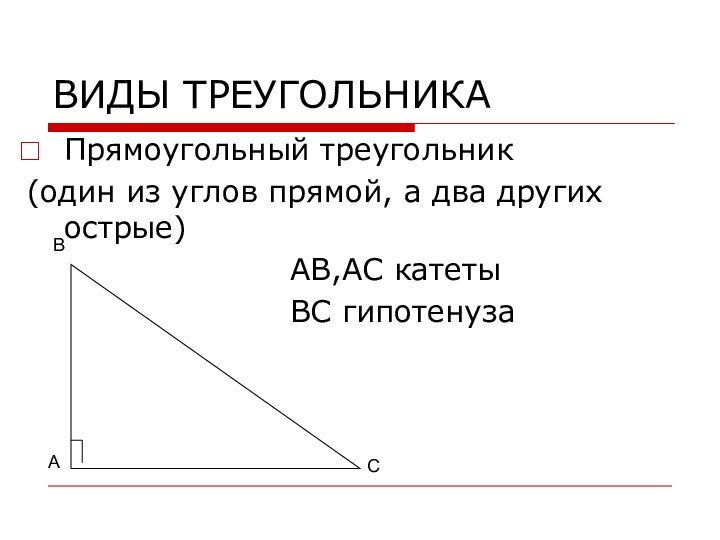
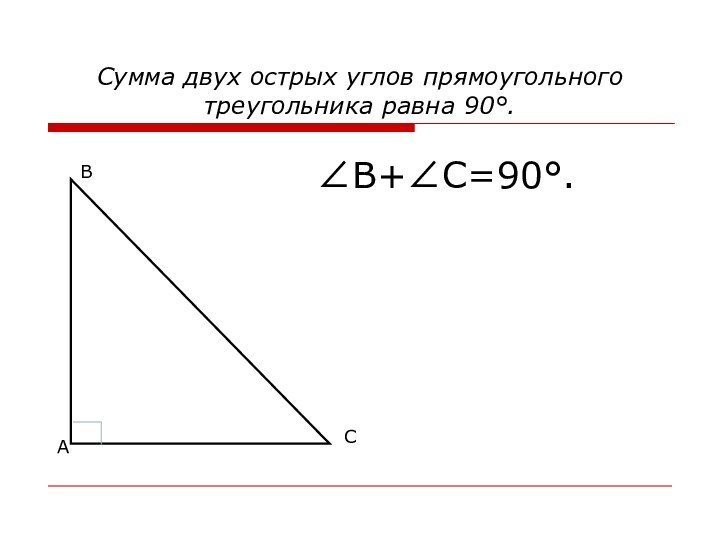
А
В
С
А
С
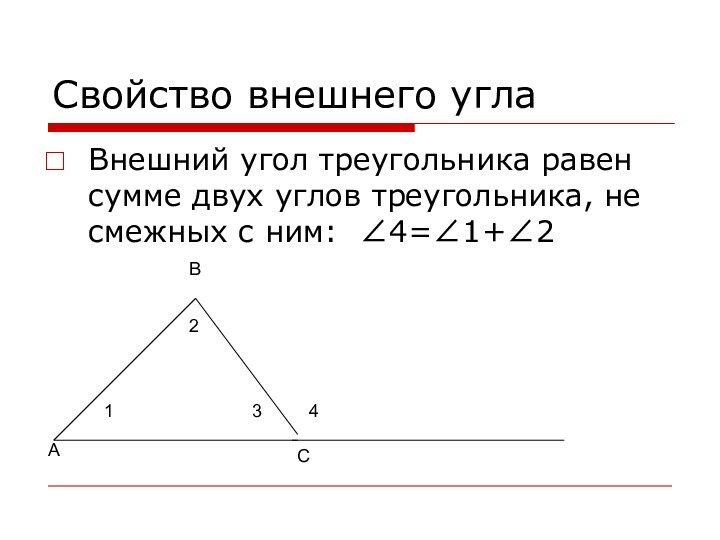
В
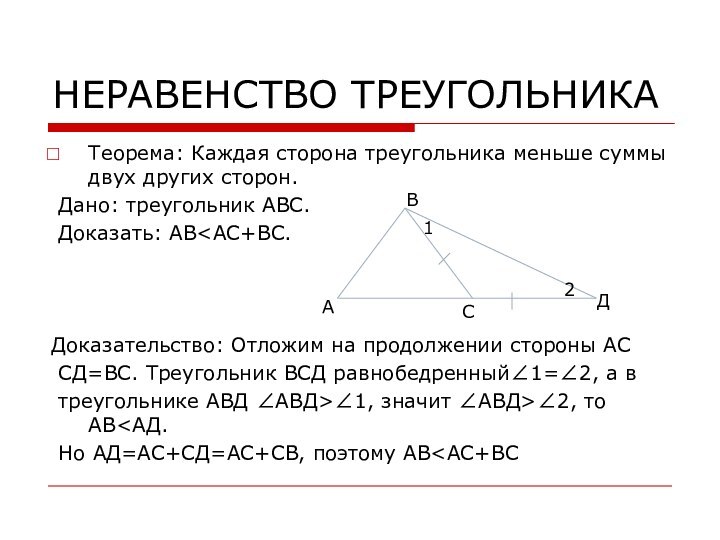
2
1
В
А
С
Д
Рассмотрим треугольник АВС, где ∠А=90°, ∠В=30° и ∠С=60°. Докажем, что АС=½ВС.
Приложим к треугольнику АВС равный ему
треугольник АВД. Получим
треугольник ВСД, ∠В=∠Д=60°,
поэтому ДС = ВС, но АС= ½ ДС,
значит АС = ½ ВС.
6
В
Д
С
А
30°
30°
60°
60°
1
В
С
А
Д
1
2
3
4