Презентация на тему Свойства степени с натуральным показателем

= 0
3) 3x2 + 10 = 0
4) 5x2 =

0
5) 2x2 – 7x = 0

 

х2

– 16 = 0,

3x2 + 10 =0 ,

5x2 =0,
2x2 - 7x = 0, .

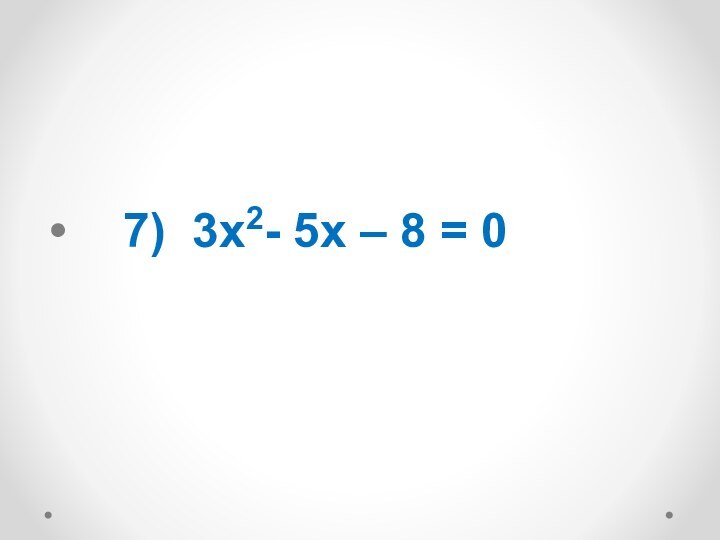
х1=0, x2 =-4

х1,2 =+ 4

решений нет

x1 = 0

x1 =0, x2 =3,5

= 0
3) 3x2 + 10 = 0
4) 5x2 =

0
5) 2x2 – 7x = 0

─ корни уравнения х2 + px + q =0,

то x1 + x2 = ─ p х1· x2 = q

Теорема Виета: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

6) х2-2х-3=0
х1 = - 1 и х2 = 3

- Неприведенные 7) 3x2- 5x – 8 = 0

c = 0, a ≠0
 

0

Фонтене-ле-Конт, недалеко от знаменитой крепости Ла-Рошель. Получил юридическое образование,

но стал секретарём и домашним учителем. Тогда Виет очень увлёкся изучением астрономии и тригонометрии и даже получил некоторые важные результаты.
В 1571 году Виет переехал в Париж, где возобновил адвокатскую практику а позже стал советником парламента в Британии. Занял должность тайного советника сначала при короле ГенрихеIII,а затем при Генрихе IV.
Одним из самых замечательных достижений Виета на королевской службе была разгадка шифра из 500 знаков, меняющихся время от времени, которыми пользовались испанцы.
Из-за религиозных противоречий был отстранён от двора и вернулся на службу лишь после разрыва короля с герцогами Гизами, через четыре года.
Эти годы оказались чрезвычайно плодотворными для Виета. Математика стала его единственной страстью, где он работал самозабвенно. Именно тогда он начал большой труд, который назвал“Искусство анализа или Новая алгебра”. Книгу завершить не удалось, но главное было написано. И это главное определило развитие всей математики Нового времени.

в городе Багдаде, их вывел приглашённый математик из Хорезм(Ныне

территория Узбекистана) Мухаммед бен-Муса Ал-Хорезми. В отличие от греков, решавших квадратные уравнения геометрическим путем, он мог решить любые квадратные уравнения по общему правилу (найти положительные корни). Если у греков было геометрическое решение, то метод Ал-Хорезми почти алгебраический.

не только первой, но и второй степени ещё в

древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а так же с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Правило решения уравнений, изложенное в вавилонских текстах, совпадает с современным. Несмотря на высокий уровень развития алгебры в Вавилонии, в их текстах отсутствует понятие отрицательного числа и общие методы решения квадратных уравнений.

уже в 499 году.
В Древней Индии были распространены публичные

соревнования в решении трудных задач.

В одной из старинных индийских книг говорится по поводу таких соревнований следующее: “Как солнце блеском своим затмевает звёзды, так учёный человек затмит славу другого в народных собраниях, предлагая и решая алгебраические
задачи”.

квадратных уравнений в Европе были
впервые изложены в 1202

году итальянским математиком
Леонардо Фибоначчи.

Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду аx2 + bx + c = 0,было
сформулировано в Европе лишь в 1544
году немецким математиком
Михаэлем Штифелем.

умели решать древнегреческие математики, сводя их решение к геометрическим

построениям. Правило решения квадратных уравнений, приведенных к виду
aх2 + bx + c = 0, где а ≠ 0,дал индийский ученый Брахмагупта(7век).

Вывод формулы корней квадратного уравнения в общем виде имеется у Виета, однако он признавал только положительные корни. Итальянские математики в16 веке учитывали помимо положительных и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других учёных способ решения квадратных уравнений принимает современный вид.

решить математики Древнего
Египта. Неполные квадратные уравнения умели решать вавилоняне
(около

2 тыс. лет до н.э.). Некоторые виды квадратных уравнений,
сводя их решение к геометрическим построениям, могли решать древнегреческие математики. Примеры решения уравнений без обра- щения к геометрии даёт Диофант Александрийский (III век).

Правило решения квадратных уравнений дал индийский учёный
Брахмагупта (VII век).

Общее правило решения квадратных уравнений было
сформулировано немецким математиком М. Штифелем.
Выводом формулы решения квадратных уравнений общего вида занимался Ф. Виет.

задачи– такое же искусство, как умение плавать и бегать.

Ему можно научиться только путем подражания или упражнения».
Д. Пойа

которого 135 см2.
Но вот размеры сторон он забыл.

Единственное, что он помнил, что одна сторона такой фигуры больше другой на 6 см. Определите, каковы стороны такого прямоугольника, чтобы школьник мог нарисовать заданную фигуру.

2вариант
1. Чему равна сумма корней квадратного уравнения
х2+4х - 5=0 х2 + 5х +3=0
2. Найти произведение корней квадратного уравнения
х2+4х - 5=0 х2 + 5х +3=0
3. Сколько корней имеет квадратное уравнение
2х2+5х-7=0 9х2-6х+2=0
4. Найдите корни квадратного уравнения
4х2-3х-1=0 3х2-5х+2=0

2вариант
1. Сумма корней квадратного уравнения равна
х2+4х -5=0 (- 4) х2 + 5х +3=0 (- 5)
2. Произведение корней квадратного уравнения равно
х2+4х -5=0 (-5) х2 + 5х +3=0 (3)
3. Сколько корней имеет квадратное уравнение
2х2+5х-7=0 (2) 9х2-6х+2=0 (0)
4. Найдите корни квадратного уравнения
4х2-3х-1=0 (1; 0,25) 3х2-5х+2=0 (1; 2/3)

вы что –то нового на уроке?
Довольны ли вы своей

работой на уроке?
Вам было интересно на уроке?

к знаниям всегда
Успешною дорога.