Слайд 2
Технологии ИИ
ПОНЯТИЕ НЕЧЕТКОГО МНОЖЕСТВА
Основой четкого множества является характеристическая
функция A
Элемент либо принадлежит множеству (A=1), либо нет (A=0).
Третьего не дано (пресловутый принцип исключения третьего).
Следствием теории четких множеств является булева логика, все то множество схем рассуждений и выводов, которые опираются на понятие характеристической функции.
Слайд 3
Технологии ИИ
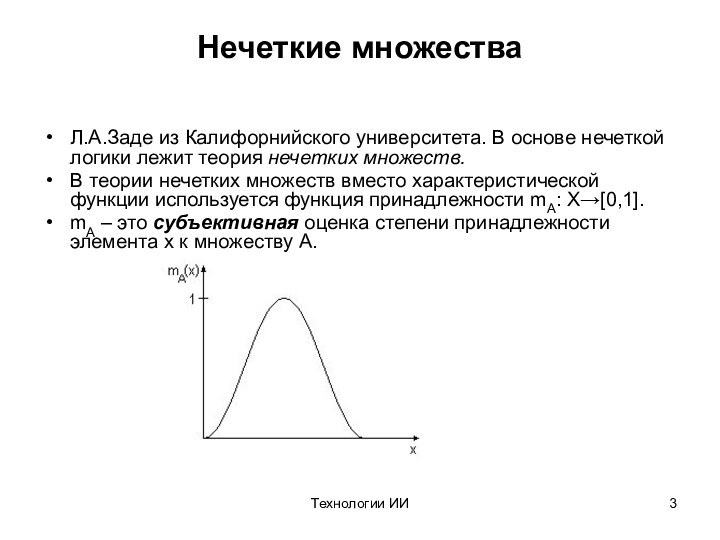
Нечеткие множества
Л.А.Заде из Калифорнийского университета. В основе
нечеткой логики лежит теория нечетких множеств.
В теории нечетких множеств
вместо характеристической функции используется функция принадлежности mA: X[0,1].
mA – это субъективная оценка степени принадлежности элемента x к множеству A.
Слайд 4
Технологии ИИ
Примеры
Понятие "маленького числа" (на множестве от нуля
до 10) можно определить в виде нечеткого множества
A =
1/0+1/1+0.8/2+0.5/3+0.1/4+0/5+0/6+0/7+0/8+0/9+0/10
Интерпретация:
число 0 однозначно является маленьким (mA=1),
число 1 – тоже
число 2 – уже не очень маленькое (mA=0.8). Это тем более касается чисел 3 (mA=0.5) и 4 (mA=0.1, т.е. 4 – это почти наверняка немаленькое число).
числа от 5 до 10 – однозначно не маленькие (mA=0).
Лингвистические переменные
Не обязательно использовать числовые оценки. Зачастую, с точки зрения взаимодействия с пользователем, целесообразнее использовать т.н. "лингвистические переменные" – термины типа "много", "мало", "высокий", "низкий" и т.п.
Слайд 5
Технологии ИИ
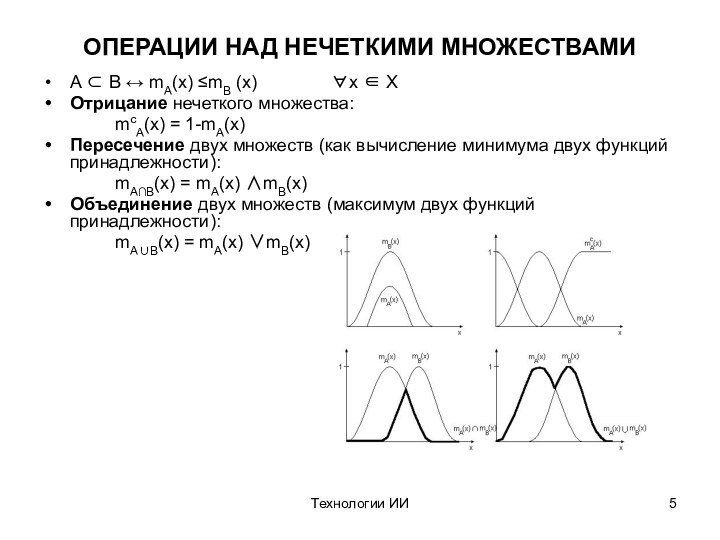
ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
A B
mA(x) mB (x) x X
Отрицание нечеткого множества:
mcA(x) =
1-mA(x)
Пересечение двух множеств (как вычисление минимума двух функций принадлежности):
mAB(x) = mA(x) mB(x)
Объединение двух множеств (максимум двух функций принадлежности):
mAB(x) = mA(x) mB(x)
Слайд 6
Технологии ИИ
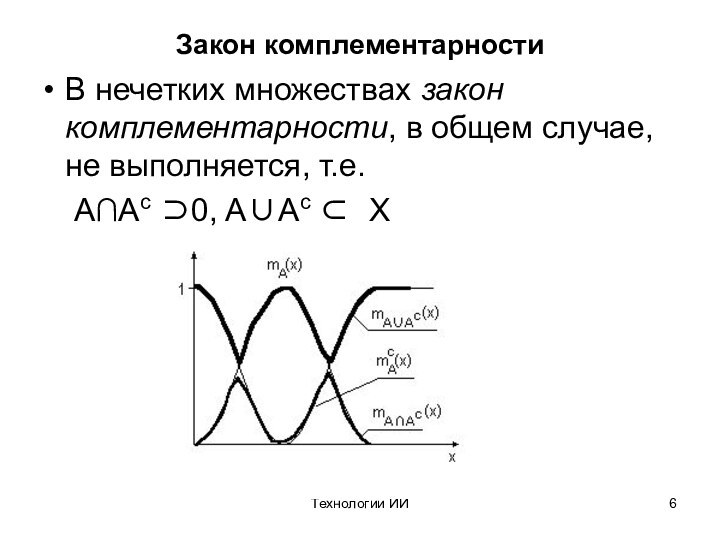
Закон комплементарности
В нечетких множествах закон комплементарности,
в общем случае, не выполняется, т.е.
AAc 0, AAc
X
Слайд 7
Технологии ИИ
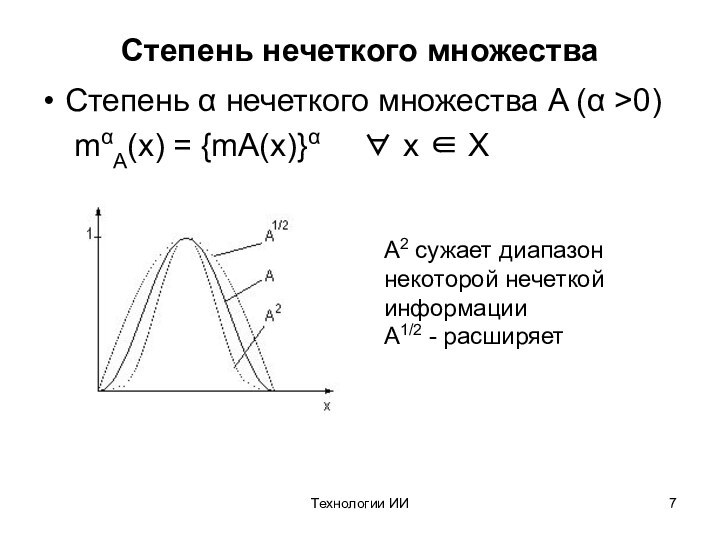
Степень нечеткого множества
Степень нечеткого множества A
( >0)
mA(x) = {mA(x)} x X
A2
сужает диапазон некоторой нечеткой информации
A1/2 - расширяет
Слайд 8
Технологии ИИ
Прочие операции
Слайд 9
Технологии ИИ
НЕЧЕТКИЕ МНОЖЕСТВА N-ГО РОДА
Для НМ первого рода
функция принадлежности выглядит как отображение
mA: X [0,1] (mA(x) [0,1], xX)
Нечеткое
множество второго рода осуществляет отображение
mA: X [0,1][0,1]
Т.е. используются не точные оценки в определенном интервале, а в качестве значений mA(x) принимается нечеткое множество над значениями оценки в [0,1].
Пусть принадлежность некоторой величины x к A оценивается в 0.8 ( НМ 1-го рода, (а)).
Если величина именно в 0.8 вызывает у нас сомнения, то можно сказать, что наша оценка лежит в интервале от 0.7 до 0.9 (б). Однако можно сказать что сама оценка представляет собой нечеткое множество. И тогда мы будем иметь дело уже с НМ 2-го рода (в).
Слайд 10
Технологии ИИ
НЕЧЕТКАЯ ЛОГИКА
От рассмотрения нечетких множеств пора переходить
к нечеткой логике.
Рассмотрим расширение операций НЕ, И, ИЛИ до
нечетких операций, называемых нечетким отрицанием, t-нормой и s-нормой соответственно.
При этом мы дадим сначала определение того, какими свойствами должна обладать операция, а затем приведем примеры возможной реализации этой операции (с точки зрения математики это красиво).
Слайд 11
Технологии ИИ
Аксиоматика определений
Слайд 12
Технологии ИИ
Аксиоматика определений
Слайд 13
Технологии ИИ
НЕЧЕТКИЕ ВЫВОДЫ И НЕЧЕТКАЯ ИМПЛИКАЦИЯ
Теперь мы имеем
полный набор нечетких логических операций.
Осталось только понять, каким
образом мы сможем применять их в процессе логического вывода.
На практике нечеткая логика применима особенно тогда, тогда мы имеем дело с приближенными рассуждениями – приближенными оценками, приближенными правилами и т.п.
Пусть, к примеру, существуют знания эксперта в виде
Что необходимо сделать в той ситуации, когда "Уровень воды довольно высокий"?
Т.е. нам надо понять, насколько необходимо открыть кран в этой ситуации (Видимо, надо "слегка открыть" кран).
Слайд 14
Технологии ИИ
Определение понятий
"Высокий" ("уровень воды высокий") :
"Высокий" =
0.7/1.5м + 0.3/1.6м + 0.7/1.7м + ... + 1/2м
+ 1/2.1м + 1/2.2м
"Открыть" ("открыть кран"):
"Открыть" = 0.1/30о + 0.2/40о + ... + 0.8/70о + 1/80о + 1/90о
"Уровень воды довольно высокий":
"Довольно высокий" = 0.5/1.6м + 1/1.7м + 0.8/1.8м + 0.2/1.9м
Итак, мы получаем следующую формальную схему:
Слайд 15
Технологии ИИ
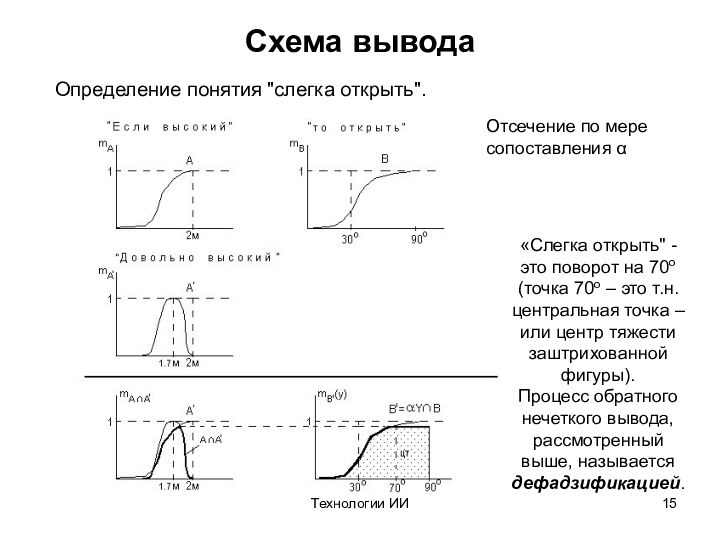
Схема вывода
Определение понятия "слегка открыть".
Отсечение по
мере сопоставления
«Слегка открыть" - это поворот на 70o
(точка 70o – это т.н. центральная точка – или центр тяжести заштрихованной фигуры).
Процесс обратного нечеткого вывода, рассмотренный выше, называется дефадзификацией.
Слайд 16
Технологии ИИ
Нечеткая импликация
Основная операция логического вывода –
это импликация. Обычно в качестве импликации используется t-норма типа
логического произведения:
x1x2 = x1x2
mR(x,y) = mAB(x,y) = (1-mA(x)+mB(y)) 1
Слайд 17
Технологии ИИ
Получение нечеткого результата вывода
Если дано знание эксперта
в виде нечеткого отношения R=AB, то процесс получения нечеткого
результата вывода B' с использованием данных наблюдения A' и знания AB можно представить как B' = A'•R = A'•(AB), где ''- т.н. композиционное правило нечеткого вывода.
В частности, имеем
Осталось определить ЦТ. В качестве ЦТ можно выбрать центр тяжести композиции максимум-минимум, использовать медианы (среднее значение) и т.п.
Слайд 18
Технологии ИИ
Пример системы нечеткого управления
Нечеткое управление скоростью
Задача
плавного торможения/разгона поезда при соблюдении условия максимально точного позиционирования
состава относительно пассажирской платформы.
Нечеткие контроллеры
Слайд 19
Технологии ИИ
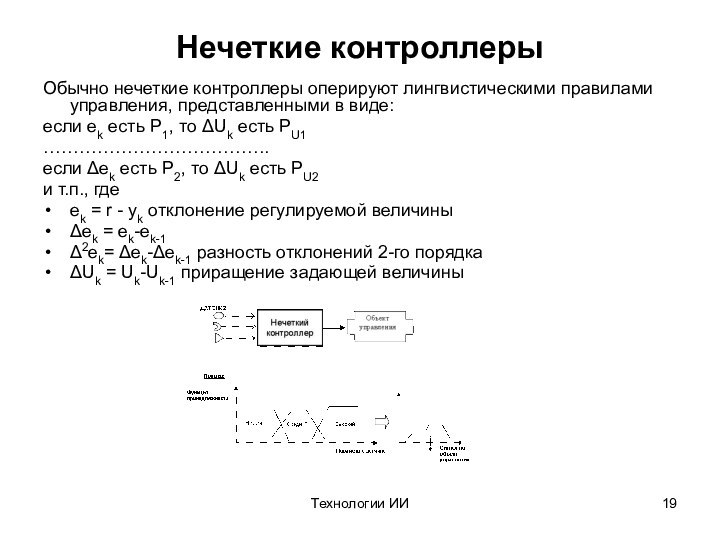
Нечеткие контроллеры
Обычно нечеткие контроллеры оперируют лингвистическими правилами
управления, представленными в виде:
если ek есть P1, то Uk
есть PU1
………………………………..
если ek есть P2, то Uk есть PU2
и т.п., где
ek = r - yk отклонение регулируемой величины
ek = ek-ek-1
2ek= ek-ek-1 разность отклонений 2-го порядка
Uk = Uk-Uk-1 приращение задающей величины
Слайд 20
Технологии ИИ
Нечеткие контроллеры
Нечеткий контроллер содержит:
блок фазификации,
базу
знаний,
блок решений
блок дефазификации.
Блок фазификации преобразует четкие величины,
измеренные на выходе объекта управления, в нечеткие величины, описываемые лингвистическими переменными в БЗ.
Блок решений использует нечеткие условные правила, заложенные в БЗ, для преобразования нечетких входных данных в требуемые управляющие воздействия также нечеткого характера.
Блок дефазификации преобразует нечеткие данные с выхода блока решений в четкую величину, которая используется для управления объектом.
Аппаратный реализация
Программная (эмуляция)
Гибридная
Слайд 21
Технологии ИИ
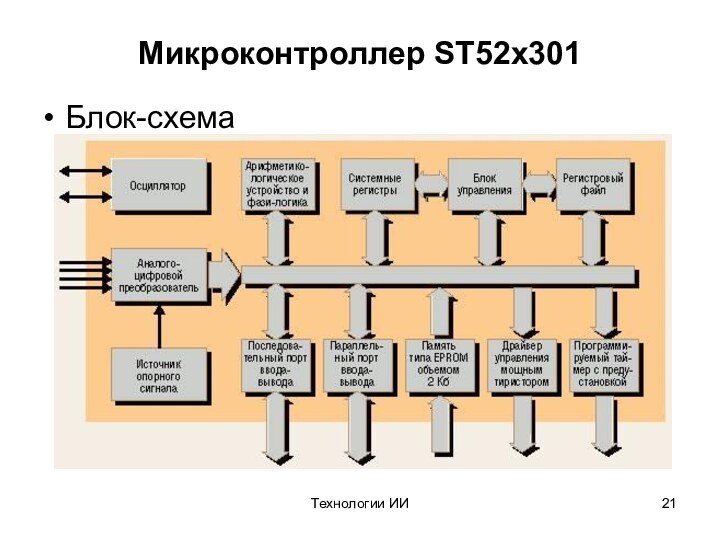
Микроконтроллер ST52x301
Блок-схема
Слайд 22
Технологии ИИ
Задача управления автомобилем
Передаточная функция объекта управления (блок
управления + карбюратор + автомобиль) имеет вид
Основной задачей СУ
может является регулирование по заданному закону момента Мс, в зависимости от угла открытия дроссельной заслонки, частоты вращения коленчатого вала, его ускорения (замедления) и включения в коробке передач той или иной передачи.