Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Тела вращения

Содержание

2. ЦилиндрКонусШар и сфераТела вращенияСодержаниеЛевый клик по названию раздела
3. Тело вращения – это пространственная фигура, полученная
4. Задание1) Приведите примеры из окружающего мира тел,
5. ЦилиндрЗададим две параллельные плоскости α и β.
6. ЦилиндрЦилиндр – это тело, которое описывает прямоугольник
7. Виды цилиндровПрямой круговойПрямой некруговойНаклонный круговойЗамечание: В школьном курсе геометрии по умолчанию рассматривается прямой круговой цилиндрпарабола
8. Сечения цилиндраОсевое сечение: Плоскость сечения содержит
9. Площадь поверхности цилиндраДля вывода формулы площади полной
10. Решение устных задач с цилиндром1)Во сколько раз
11. Решение устных задач с цилиндром3) Осевые сечения
12. КонусЗададим плоскость α и точку С вне
13. Конус – это тело, которое описывает прямоугольный
14. Конические сечения1) Если плоскость пересекает все образующие
15. Сечения конусаОсевое сечение. Плоскость сечения содержит
16. Площадь поверхности конусаДля вывода формулы площади полной
17. Площадь сектораВычисляя боковую поверхность конуса вписываем в
18. Решение устных задач с конусом1)Во сколько раз
19. Определение шараШаром называется тело, которое состоит из
20. Сечения шараСечение шара, проходящее через его центр.
21. Взаимное расположение сферы и плоскостиd – расстояние
22. Взаимное расположение сферы и плоскостиd – расстояние
23. Взаимное расположение сферы и плоскостиd – расстояние
24. Решение задач1)Вычислить площадь поверхности шара изображенного на
25. Географическая справкаГеографические широты могут иметь значение от
26. ЛитератураАтанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и
27. Скачать презентацию
28. Похожие презентации

ЦилиндрКонусШар и сфераТела вращенияСодержаниеЛевый клик по названию раздела

Тело вращения – это пространственная фигура, полученная вращением плоской ограниченной области вместе

Задание1) Приведите примеры из окружающего мира тел, похожих на тело полученное вращением

ЦилиндрЗададим две параллельные плоскости α и β. В плоскости α расположим окружность

ЦилиндрЦилиндр – это тело, которое описывает прямоугольник при вращении около оси, содержащей

Виды цилиндровПрямой круговойПрямой некруговойНаклонный круговойЗамечание: В школьном курсе геометрии по умолчанию рассматривается прямой круговой цилиндрпарабола

Сечения цилиндраОсевое сечение: Плоскость сечения содержит ось цилиндра и перпендикулярна основаниям.

Площадь поверхности цилиндраДля вывода формулы площади полной поверхности цилиндра потребуется развертка цилиндра.

Решение устных задач с цилиндром1)Во сколько раз увеличится боковая поверхность цилиндра, если

Решение устных задач с цилиндром3) Осевые сечения двух цилиндров равны. Равны ли

КонусЗададим плоскость α и точку С вне этой плоскости. В плоскости α

Конус – это тело, которое описывает прямоугольный треугольник при вращении вокруг оси,

Конические сечения1) Если плоскость пересекает все образующие конической поверхности, то в сечении

Сечения конусаОсевое сечение. Плоскость сечения содержит ось конуса и перпендикулярна основанию.

Площадь поверхности конусаДля вывода формулы площади полной поверхности конуса потребуется его развертка.

Площадь сектораВычисляя боковую поверхность конуса вписываем в данную формулу новые обозначения и

Решение устных задач с конусом1)Во сколько раз увеличится боковая поверхность конуса, если

Определение шараШаром называется тело, которое состоит из всех точек пространства, находящихся на

Сечения шараСечение шара, проходящее через его центр. В сечении – Сечение плоскостью,

Взаимное расположение сферы и плоскостиd – расстояние от центра сферы до плоскости,

Решение задач1)Вычислить площадь поверхности шара изображенного на рисунке.R = ОА, Найдем ОА

Географическая справкаГеографические широты могут иметь значение от 0° до 90°. Географическая широта

ЛитератураАтанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11: Учеб. для

Интернет ресурсО географической широтеГеографические координатыИзображение сечений моделей цилиндраИзображение тел вращенияЮлаВолчокИгрушкаИзображение тораКолокольчикПесочные часыКартинка

Слайды презентации

Слайд 2
Цилиндр
Конус
Шар и сфера
Тела вращения
Содержание
Левый клик по названию раздела

Слайд 3 Тело вращения – это пространственная фигура, полученная вращением

Тело вращения – это пространственная фигура, полученная вращением плоской ограниченной области

плоской ограниченной области вместе со своей границей вокруг оси,

лежащей в той же плоскости.

Определение тела вращения

Слайд 4 Задание
1) Приведите примеры из окружающего мира тел, похожих

Задание1) Приведите примеры из окружающего мира тел, похожих на тело полученное

на тело полученное вращением треугольника вокруг оси, содержащей его

сторону:

Слайд 5 Цилиндр

Зададим две параллельные плоскости α и β. В

ЦилиндрЗададим две параллельные плоскости α и β. В плоскости α расположим

плоскости α расположим окружность некоторого радиуса. Если из каждой

точки окружности провести взаимно параллельные прямые пресекающие плоскость β, то в плоскости β получится окружность такого же радиуса. Отрезки прямых, заключенных между параллельными плоскостями образуют в этом случае цилиндрическую поверхность.

Цилиндр – это тело, заключенное между двумя кругами расположенными в параллельных плоскостях и цилиндрической поверхностью.

Слайд 6 Цилиндр
Цилиндр – это тело, которое описывает прямоугольник при

ЦилиндрЦилиндр – это тело, которое описывает прямоугольник при вращении около оси,

вращении около оси, содержащей его сторону.

Верхний и нижний круги

– это основания цилиндра.

Прямая проходящая через центры кругов – это ось цилиндра.

Отрезок параллельный оси цилиндра, концы которого лежат на окружностях основания – это образующая цилиндра.

Радиус основания - это радиус цилиндра.

Высота цилиндра - это перпендикуляр между основаниями цилиндра.

Слайд 7 Виды цилиндров
Прямой круговой
Прямой некруговой
Наклонный круговой
Замечание: В школьном курсе

геометрии по умолчанию рассматривается прямой круговой цилиндр
парабола

Слайд 8
Сечения цилиндра
Осевое сечение: Плоскость сечения содержит ось

цилиндра и перпендикулярна основаниям. В сечении –

Замечание: Секущая

плоскость может располагаться по-разному, рассмотрим некоторые виды сечений

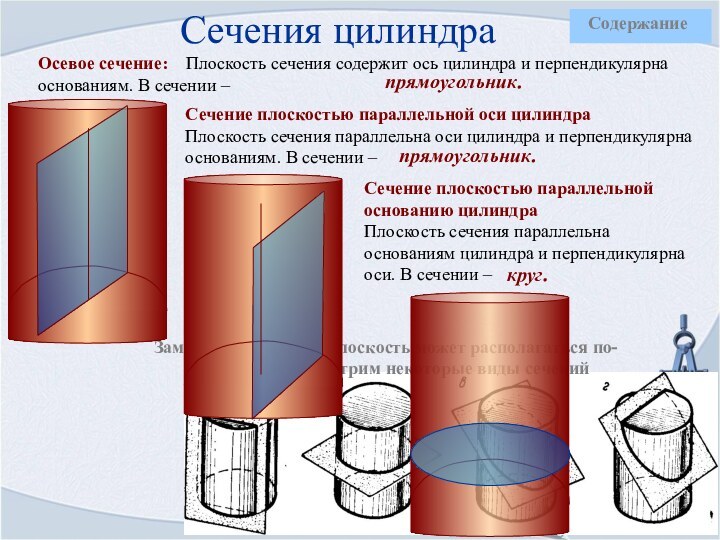
Сечение плоскостью параллельной оси цилиндра Плоскость сечения параллельна оси цилиндра и перпендикулярна основаниям. В сечении –

Сечение плоскостью параллельной основанию цилиндра Плоскость сечения параллельна основаниям цилиндра и перпендикулярна оси. В сечении –

прямоугольник.

круг.

Слайд 9
Площадь поверхности цилиндра
Для вывода формулы площади полной поверхности

Площадь поверхности цилиндраДля вывода формулы площади полной поверхности цилиндра потребуется развертка

цилиндра потребуется развертка цилиндра.
Sполн = 2πR(R +

прямоугольник.

Боковая поверхность цилиндра есть …

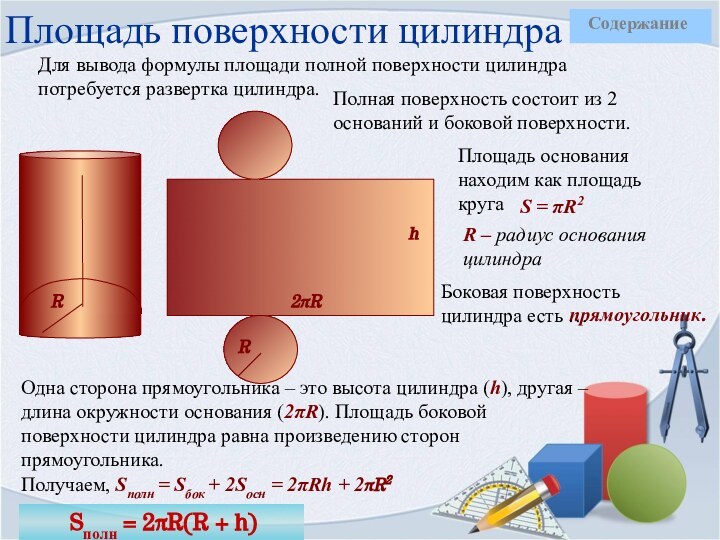
Полная поверхность состоит из 2 оснований и боковой поверхности.

Площадь основания находим как площадь круга

S = πR2

R – радиус основания цилиндра

Одна сторона прямоугольника – это высота цилиндра (h), другая – длина окружности основания (2πR). Площадь боковой поверхности цилиндра равна произведению сторон прямоугольника.

Получаем, Sполн = Sбок + 2Sосн = 2πRh + 2πR2

2πR

Слайд 10 Решение устных задач с цилиндром
1)Во сколько раз увеличится

Решение устных задач с цилиндром1)Во сколько раз увеличится боковая поверхность цилиндра,

боковая поверхность цилиндра, если его высота увеличится в 5

раз, а радиус основания останется прежним?

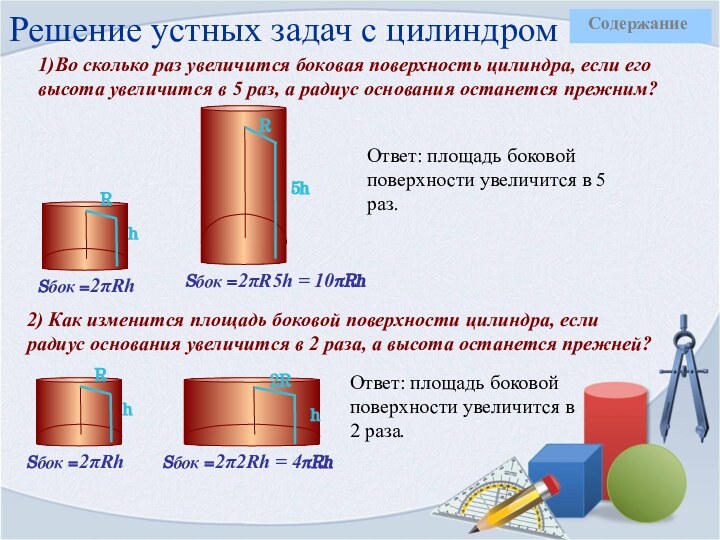
Ответ: площадь боковой поверхности увеличится в 5 раз.

Sбок =2πRh

Sбок =2πR5h = 10πRh

2) Как изменится площадь боковой поверхности цилиндра, если радиус основания увеличится в 2 раза, а высота останется прежней?

Sбок =2πRh

Sбок =2π2Rh = 4πRh

Ответ: площадь боковой поверхности увеличится в 2 раза.

Слайд 11 Решение устных задач с цилиндром
3) Осевые сечения двух

Решение устных задач с цилиндром3) Осевые сечения двух цилиндров равны. Равны

цилиндров равны. Равны ли высоты этих цилиндров?

Ответ: нет
Sсеч

=2R·h

4) Стороны прямоугольника равны 4 см и 5 см. Найдите площадь поверхности тела, полученного при вращении этого прямоугольника вокруг меньшей стороны.

5 см

R=5 см, h=4см

Sполн =2πR(h +R)= 2π· 5 ·(4 + 5) =90π

Ответ: площадь полной поверхности равна 90 π см2

Sсеч =h·2R

4 см

Слайд 12 Конус

Зададим плоскость α и точку С вне этой

КонусЗададим плоскость α и точку С вне этой плоскости. В плоскости

плоскости. В плоскости α расположим окружность некоторого радиуса. Проведем

прямые проходящие через точку С и все точки окружности. Поверхность, образованная отрезками с концами на окружности и в точке С образуют коническую поверхность.

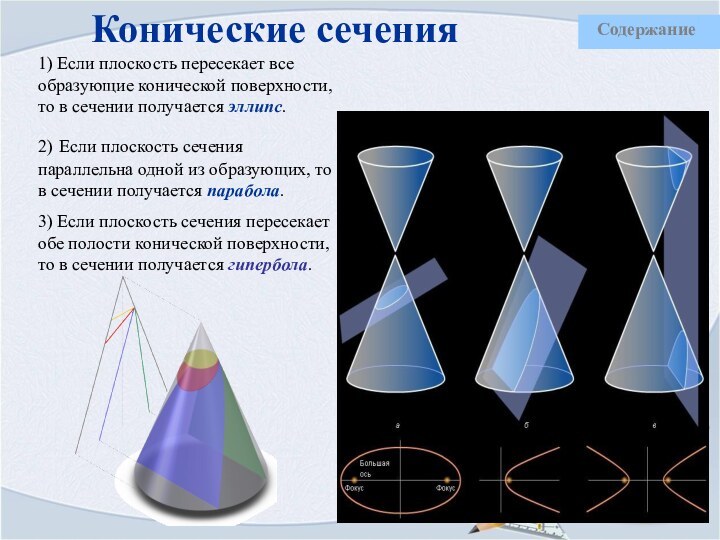
Конус – это тело, ограниченное конической поверхностью и кругом, включая окружность.

Слайд 13 Конус – это тело, которое описывает прямоугольный треугольник

Конус – это тело, которое описывает прямоугольный треугольник при вращении вокруг

при вращении вокруг оси, содержащей его катет.

Круг –

это основание конуса.

Прямая проходящая через центр круга и вершину конуса – есть ось конуса.

Отрезок соединяющий вершину с любой точкой окружности основания – это образующая конуса.

Радиус основания - это радиус конуса.

Высота конуса - это перпендикуляр, опущенный из вершины конуса к основанию.

Конус

Точка вне круга с которой соединяются все точки окружности – это вершина конуса.

Замечание: так как ось перпендикулярна основанию и проходит через вершину, то высота конуса лежит на его оси.

Слайд 14 Конические сечения
1) Если плоскость пересекает все образующие конической

Конические сечения1) Если плоскость пересекает все образующие конической поверхности, то в

поверхности, то в сечении получается эллипс.
2) Если плоскость сечения

параллельна одной из образующих, то в сечении получается парабола.
3) Если плоскость сечения пересекает обе полости конической поверхности, то в сечении получается гипербола.

Слайд 15
Сечения конуса
Осевое сечение. Плоскость сечения содержит ось

конуса и перпендикулярна основанию.
В сечении –

Сечение плоскостью

параллельной основанию конуса. Плоскость сечения параллельна основанию конуса и перпендикулярна оси.
В сечении –

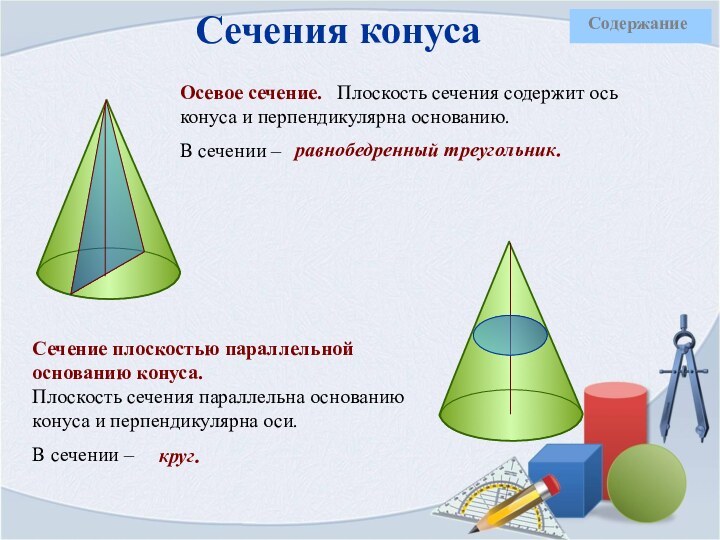
равнобедренный треугольник.

круг.

Слайд 16 Площадь поверхности конуса
Для вывода формулы площади полной поверхности

Площадь поверхности конусаДля вывода формулы площади полной поверхности конуса потребуется его

конуса потребуется его развертка.

Sполн = πR(l +

сектор.

Боковая поверхность конуса есть …

Полная поверхность состоит из основания и боковой поверхности.

Площадь основания находим как площадь круга

S = πR2

R – радиус основания цилиндра

Площадь боковой поверхности вычисляется как площадь сектора радиус которого равен длине образующей конуса (l), а дуга равна длине окружности основания (2πR). Площадь боковой поверхности конуса равна произведению радиуса на образующую и число π.

Получаем, Sполн = Sбок + Sосн = πRl + πR2

2πR

Подробнее о площади сектора

Слайд 17
Площадь сектора
Вычисляя боковую поверхность конуса вписываем в данную

Площадь сектораВычисляя боковую поверхность конуса вписываем в данную формулу новые обозначения

формулу новые обозначения и выражаем α через радиус (R)

и образующую (l). Длина дуги сектора равна длине окружности основания конуса 2πR , с другой стороны ее можно вычислить по формуле для длины дуги. Получаем равенство:

r = l

r – радиус круга, α – величина дуги в градусах, R – радиус основания конуса, l – длина образующей конуса

Выразим α и подставим в формулу площади сектора круга.

Слайд 18 Решение устных задач с конусом
1)Во сколько раз увеличится

Решение устных задач с конусом1)Во сколько раз увеличится боковая поверхность конуса,

боковая поверхность конуса, если его образующая увеличится вдвое, а

радиус основания одновременно увеличится в 3 раза?

Ответ: площадь боковой поверхности увеличится в 6 раз.

Sбок =πRl

Sбок = π 3R2l = 6πRl

2) Вычислите площадь боковой и полной поверхностей конуса, длина образующей которого равна 10 см, а радиус основания 3 см.

Sосн =πR2 = π · 32 = 9π (см2)

Sполн = 39π (см2)

Ответ: 30π см2, 39π см2

Sбок = π 3·10 = 30π (см2)

Слайд 19 Определение шара
Шаром называется тело, которое состоит из всех

Определение шараШаром называется тело, которое состоит из всех точек пространства, находящихся

точек пространства, находящихся на расстоянии, не большем данного, от

заданной точки точки.

Шар можно получить вращением полукруга вокруг оси, содержащей его диаметр.

Эта точка называется центром шара.

Расстояние от центра шара до любой точки поверхности называется – радиусом шара

Сфера – это поверхность все точки которой равноудалены от заданной точки.

Слайд 20 Сечения шара
Сечение шара, проходящее через его центр.
В

сечении –
Сечение плоскостью, не проходящей через центр.
В

сечении –

круг.

В этом случае в сечении получается круг наибольшего радиуса, его называют большой круг шара.

круг.

Теорема: Площадь поверхности шара равна четыре площади большого круга шара.

S = 4πR2

Слайд 21 Взаимное расположение сферы и плоскости
d – расстояние от

Взаимное расположение сферы и плоскостиd – расстояние от центра сферы до

центра сферы до плоскости, R – радиус сферы
d

R
Плоскость пересекает сферу и называется секущей

r – радиус сечения сферы

Вычислить радиус сечения можно используя теорему Пифагора.

Слайд 22
Взаимное расположение сферы и плоскости
d – расстояние от

центра сферы до плоскости, R – радиус сферы
d =

R
Плоскость имеет одну общую точку со сферой и называется касательной

Теорема: Радиус сферы проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Слайд 23
Взаимное расположение сферы и плоскости
d – расстояние от

центра сферы до плоскости, R – радиус сферы
d >

R
Плоскость не имеет общих точек со сферой.

Слайд 24 Решение задач
1)Вычислить площадь поверхности шара изображенного на рисунке.

R

Решение задач1)Вычислить площадь поверхности шара изображенного на рисунке.R = ОА, Найдем

= ОА,
Найдем ОА из ΔАСО.
S =4πR2
30°

6
О
С
А

Ответ: S =

192π ед2

Слайд 25 Географическая справка
Географические широты могут иметь значение от 0°

Географическая справкаГеографические широты могут иметь значение от 0° до 90°. Географическая

до 90°. Географическая широта 90° находится у полюсов.
Под географической

широтой понимают величину дуги от экватора к северу или к югу до заданной точки. Она тоже измеряется в градусах, так как широта точки есть угол между отвесной линией, проходящей через эту точку, и плоскостью экватора.

Северный полярный круг находится в 66°33′44″ (66,5622°) к северу от экватора.

Слайд 26 Литература

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

ЛитератураАтанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11: Учеб.

Геометрия, 10-11: Учеб. для общеобразоват. учреждений. – М.: Просвещение,

2010.
Бевз Г.П. и др. Геометрия: Учеб. для 7-11 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.
Глейзер Г.Д. Геометрия: Учеб. пособие для 10-12 кл.веч. (смен.) шк. и самообразования. – М.: Просвещение, 1989.
Клопский В.М., Скопец З.А., Ягодовский М.И. Геометрия: Учеб. пособие для 9 и 10 классов. – М.: Просвещение, 1980.