Презентация на тему Теорема Эйлера и ее применение

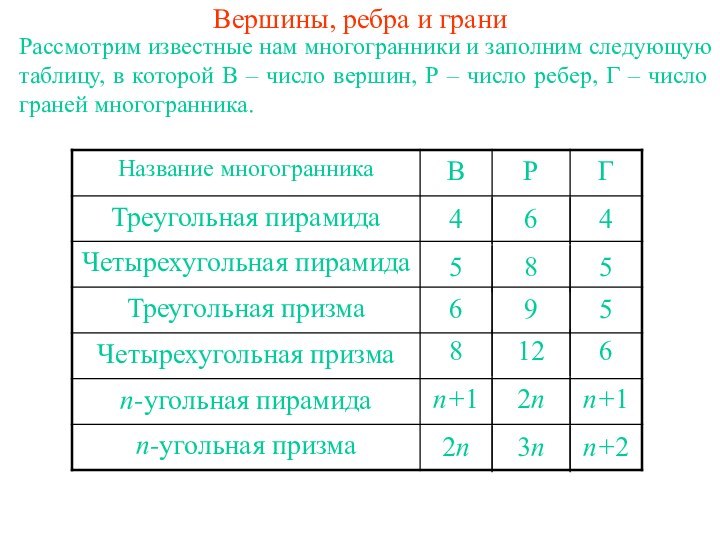
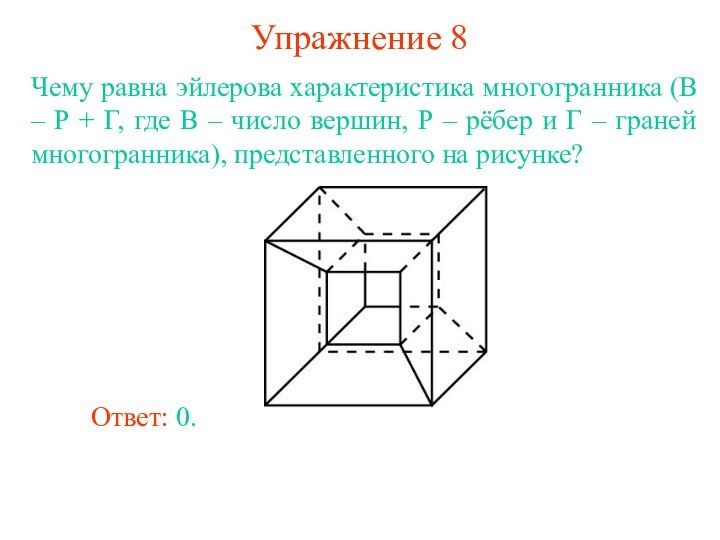
всех выбранных многогранников имеет место равенство В - Р

+ Г = 2. Оказывается, что это равенство справедливо не только для рассмотренных многогранников, но и для произвольного выпуклого многогранника. Впервые это свойство выпуклых многогранников было доказано Леонардом Эйлером в 1752 году и получило название теоремы Эйлера.

Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство
В - Р + Г = 2,
где В - число вершин, Р - число ребер и Г - число граней данного многогранника.

имеют три общих колодца. Можно ли провести непересекающиеся дорожки

от каждого дома к каждому колодцу?

Ответ: Нет.

Да.

Да.

соотношение Эйлера.

у него вершин и граней, если он имеет: а)

12 ребер; б) 15 ребер?

Ответ: а) В = 6, Г = 8;

б) В = 7, Г = 10.

ребра. Сколько он имеет вершин и граней, если число

ребер равно: а) 12; б) 15?

Ответ: а) В = 8, Г = 6;

б) В = 10, Г = 7.

у него вершин и граней, если число ребер равно

12? Приведите пример такого многогранника.

Ответ: В = 8, Г = 6, куб.

четыре ребра. Сколько он имеет вершин и граней, если

число ребер равно 12? Приведите пример такого многогранника.

Ответ: В = 6, Г = 8, октаэдр.

Р + Г, где В – число вершин, Р

– рёбер и Г – граней многогранника), представленного на рисунке?

Ответ: 0.

выпуклого многогранника, если к одной из его граней пристроить

пирамиду? Изменится ли В – Р + Г?

Ответ: Пусть пристроена n-угольная пирамида, тогда количество вершин станет (В+1), рёбер - (Р+n), граней - (Г+n). В – Р + Г не изменится.