- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
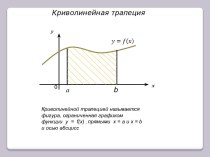
Презентация на тему Знакомство с теоремой Эйлера
Содержание
- 2. Теорема ЭйлераТеорема Эйлера- математическое утверждение, связывающее между
- 3. Леонард Эйлер
- 4. Леонард Эйлер — математик, физик
- 5. Периоды жизни20 октября 1720 года, Эйлер стал
- 6. Суть теоремыРассмотрим многогранники известные нам из школьной
- 7. Несмотря на различия самих многогранников и различия
- 8. Теорема Эйлера для простых многогранниковПусть G={r| r=(x,y,z)}
- 9. Обязательные условия, выполняемые при геоморфизме:1.Каждой точке r
- 10. Таким образом, можно сказать, что геоморфизм- это
- 11. Нетрудно показать также, что замкнутая ломаная линия
- 12. Простые многогранникиМногогранники называют простыми, если их поверхность
- 13. Докажем теорему Эйлера для простых многогранников. Пусть
- 14. Для нахождения Э(Z1) будем последовательно упрощать область
- 15. Самым поучительным в приведенном доказательстве является то,
- 16. Приложения теоремы ЭйлераТеорему Эйлера историки математики называют
- 17. Совокупность вершин и соединяющих их ребер на
- 18. Эти ребра образуют на плоскости многоугольник, подразделенный
- 19. Другой задачей-головоломкой, связанной с именем Эйлера, была
- 20. Эта задача связана с другими головоломкам, суть
- 21. На рисунке изображен граф, соответствующий задаче о
- 22. ЗаключениеОзнакомившись с теоремой Эйлера и ее приложениями
- 23. Скачать презентацию
- 24. Похожие презентации





















Слайд 3
Леонард Эйлер (1707-1783)
Эта
теорема была открыта Рене Декартом еще в 1640 году,
затем забыта более чем на сто лет и лишь в 1752 году приоткрыта российским математиком Леонардом Эйлером, имя которого она носит.В 2007 году исполнилось 214 лет со дня смерти Леонарда Эйлера- одного из величайших математиков мира, работы которого оказали решающее влияние на развитие многих современных разделов математики. Эйлер долгое время жил и работал в России, был действительным членом Петербургской Академии наук, оказал большое влияние на развитие русской математической школы и в деле подготовки кадров ученых математики и педагогов России. При жизни им опубликовано 530 книг и статей, а сейчас их известно уже более 800. Причем последние 12 лет своей жизни Эйлер тяжело болел, ослеп на правый глаз и, несмотря на тяжелый недуг он продолжал работать и творить, он отнесся к этому с величайшим спокойствием: «Теперь я меньше буду отвлекаться от занятий математикой». Это лишний раз доказывает его феноменальную работоспособность (он просто не мог не заниматься математикой или ее приложениями.
Слайд 4 Леонард Эйлер — математик, физик
механик и астроном
Эйлер принадлежит к числу гениев, чьё
творчество стало достоянием всего
человечества. До сих пор школьники всех
стран изучают тригонометрию и логарифмы
в том виде, какой придал им Эйлер.
Студенты проходят высшую математику по
руководствам, первыми образцами которых
явились классические монографии Эйлера.
Он был прежде всего математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук.
Слайд 5
Периоды жизни
20 октября 1720 года, Эйлер стал студентом
факультета искусств Базельского университета.
4 июня 1724 года, Эйлер произнёс
по латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона — и был удостоен учёной степени магистра.5 апреля 1727 года, Эйлер навсегда покидает Швейцарию, по совету братьев Бернулли его пригласили стать адъюнктом по физиологии в Санкт-Петербурге.
1733 год. 26-летний Леонард Эйлер женился на дочери живописца Екатерине Гзель, которой в это время тоже было 26 лет.
1736 год. Издано двухтомное сочинение «Механика, или наука о движении, в аналитическом изложении».
1741 год. В соответствии с поданным Эйлером прошением, он был «отпущен от Академии» и утверждён почётным академиком. Он обещал по мере своих сил помогать Петербургской Академии — и действительно помогал весьма существенно все 25 лет, пока не вернулся обратно в Россию. В июне 1741 г. Леонард Эйлер с женой, двумя сыновьями и четырьмя племянниками прибыл в Берлин.
15 апреля 1707 года, родился Леонардо Эйлер.
1757 год. Эйлер впервые в истории нашёл формулы для определения критической нагрузки при сжатии упругого стержня. Однако в те годы эти формулы не могли найти практического применения.
30 апреля 1766 года. Эйлер получает разрешение на выезд из Берлина в Россию.
1771 год. Сгорела библиотека со множеством трудов Леонардо Эйлера, но в течении некоторого времени Эйлер восстанавливает утраченные труды по памяти. В сентябре того же года в Санкт-Петербург прибыл известный немецкий окулист барон Венцель, который согласился сделать Эйлеру операцию — и удалил с левого глаза катаракту. Но вся операция заняла 3 минуты — и Эйлер снова стал видеть! Искусный окулист предписал беречь глаз от яркого света, не писать, не читать — лишь постепенно привыкать к новому состоянию. Эйлер нарушил эти наставления и на следующий день начал писать свои труды дальше, окончательно потеряв зрение.
1773 год. Умерла жена Эйлера.
В сентябре 1783 г. учёный стал ощущать головные боли и слабость. 7 сентября после обеда, проведённого в кругу семьи, беседуя с А. И. Лекселем об недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо. Эйлер успел произнести «Я умираю» — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг. «Эйлер перестал жить и вычислять». Его похоронили на Смоленском кладбище в Петербурге. Надпись на памятнике гласила: «Леонарду Эйлеру — Петербургская Академия».
Назад
Слайд 6
Суть теоремы
Рассмотрим многогранники известные нам из школьной программы-
тетраэдр и куб, которые имеют вершины(В), ребра(Р) и грани(Г).
Составим для них табличку:Слайд 7 Несмотря на различия самих многогранников и различия их
величин В,Г, и Р, значение Э остается постоянным и
равным 2. значит, имеет место неравенство:В+Г-Р= 2
которое и называется теоремой Эйлера для многогранников.
Слайд 8
Теорема Эйлера для простых многогранников
Пусть G={r| r=(x,y,z)} и
G’={r’| r’=(x’,y’,z’)} – два точечных множества в трехмерном пространстве
(не исключая возможности того, что G и G’ лежат на каких-либо кривых или принадлежат каким-либо плоскостям).
Слайд 9
Обязательные условия, выполняемые при геоморфизме:
1.Каждой точке r из
G отображение f(r) ставит в соответствие единственную точку r’
из G’ и для любой точки r’ из G’ существует единственная точка r из G, для которой f(r)= r’.2.Для любых r1,r2 из G, r’1= f(r1), r’2= f(r2):
если |r1- r2|>0, то |r’1- r’2|>0;
если |r’1- r’2|>0, то |r1- r2|>0.
Условие1 есть требование взаимной однозначности отображения r’=f(r): разные точки под действием f(r) переходят в разные.
Условие2 есть требование непрерывности отображения f(r) и его обратного f-1(r’): близкие точки r1 и r2 из G должны отображаться в близкие точки из G’ и, наоборот, близкие точки r’1 и r’2 из G’ должны иметь близкие прообразы r1 и r2 в G.
Слайд 10 Таким образом, можно сказать, что геоморфизм- это взаимно
однозначное и непрерывное отображение, для которого обратное тоже является
непрерывным.Примером может служить соответствие между точками поверхности куба и точками содержащей его произвольной сферы. Установим это соответствие таким образом: из произвольной точки О, лежащей строго внутри куба, проведем лучи ко всем точкам сферы и точке r пересечения луча с поверхностью куба поставим в соответствии точку r’ пересечения этого же луча с поверхностью сферы. Легко проверить, что отображение удовлетворяет требованиям 1и 2 и определению геоморфизма и , следовательно, является геоморфизмом.
Слайд 11 Нетрудно показать также, что замкнутая ломаная линия без
самопересечений гемеоморфна окружности, что парабола гемеоморфна прямой и т.д.
В то же время, например, отрезок прямой негеоморфен окружности. Действительно, если бы отрезок был гемеоморфен окружности, то отрезок с выколотой точкой был бы гемеоморфен окружности с выколотой точкой. Но это невозможно, поскольку отрезок с выколотой точкой есть множество несвязное и при геоморфизме он должен отображаться в несвязное множество, а окружность с выколотой точкой является множеством связным. Точно также можно показать, что отрезок негеоморфен кругу.В качестве распространенного и наглядного примера гомеоморфного отображения поверхности можно рассматривать ее деформацию при условии, что эта деформация не разрывает поверхности (является непрерывной) и не приводит к склеиванию различных точек (то есть является взаимно однозначной).
Слайд 12
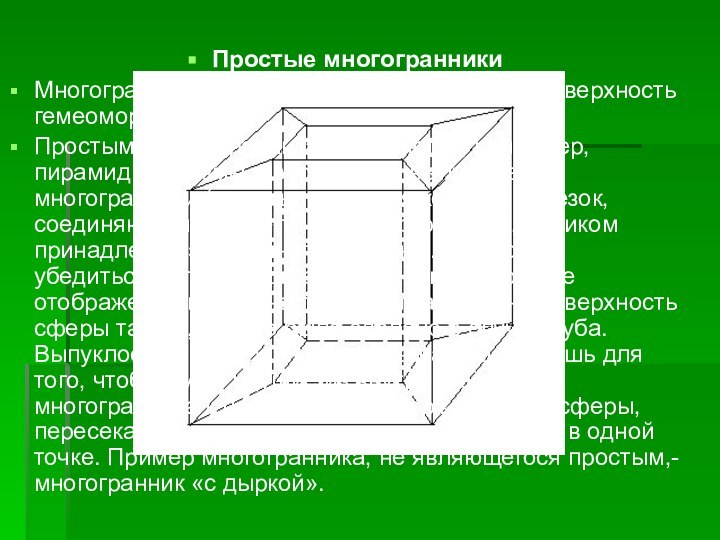
Простые многогранники
Многогранники называют простыми, если их поверхность гемеоморфна
сфере.
Простыми многогранниками являются, например, пирамиды, призмы и вообще все
выпуклые многогранники (то есть такие, для которых отрезок, соединяющий любые точки многогранника, целиком принадлежит этому многограннику). Мы можем убедиться в этом, построив явно гомеоморфное отображение поверхности многогранника на поверхность сферы так же, как это было сделано в случае куба. Выпуклость многогранника нужна нам здесь лишь для того, чтобы лучи, идущие из внутренней точки многогранника к поверхности содержащей его сферы, пересекали поверхность многогранника только в одной точке. Пример многогранника, не являющегося простым,- многогранник «с дыркой».Слайд 13 Докажем теорему Эйлера для простых многогранников. Пусть Z
– поверхность простого многогранника, В(Z ), Г(Z ) и
Р(Z ) – соответственно число вершин, граней и ребер поверхности Z, Э(Z)=В(Z)+Г(Z)+Р(Z).Мы хотим доказать, что Э(Z)=2. Отобразим гемеоморфно Z на поверхность S0 некоторой сферы. Тогда на S0 появится криволинейная сетка L0 состоящая из образов ребер многогранника; образами граней будут некоторые области на S0 ,гомеоморфные кругу, а образами вершин- точки пересечения кривых сетки L0 между собой. Сохраним за образами на сфере ребер, вершин и граней поверхности Z прежние названия. Вследствие геоморфизма поверхностей Z и S0 числа ребер Р(S0), граней Г(S0) и вершин В(S0) криволинейной сетки L0 на сфере S0 будут теми же, что у поверхности Z, и, значит, Э(S0)=Г(S0)+В(S0)-Р(S0)=Э(Z). Вырежем из поверхности сферы S0 одну грань и гемеоморфно деформируем полученную сферу с «дыркой» в плоскую области, растягивая сферу так, чтобы ребра – границы дырки составили границу полученной плоской области Z1.. Вследствие деформации сферы S0 сетка L0 на S0 трансформируется в некоторую сетку L1 на Z1. По построению, сетка L1 , имеет на одну грань меньше, чем L0, при том же количестве вершин и ребер, и, значит,Э(Z0)=Э(Z1)+1
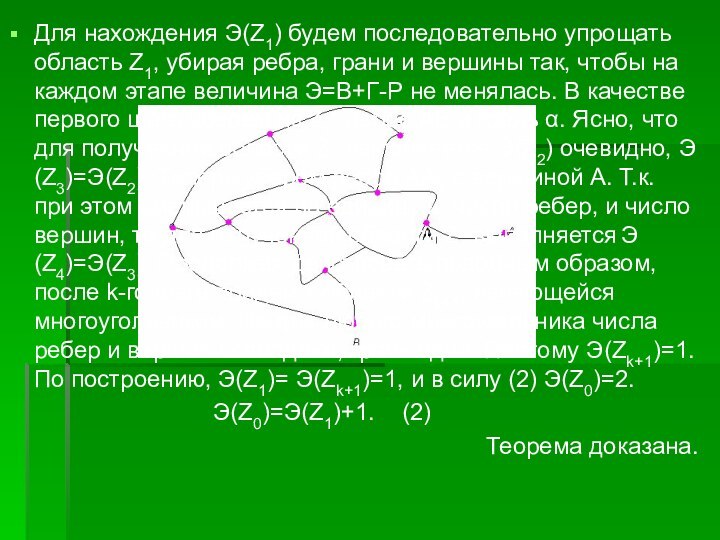
Слайд 14 Для нахождения Э(Z1) будем последовательно упрощать область Z1,
убирая ребра, грани и вершины так, чтобы на каждом
этапе величина Э=В+Г-Р не менялась. В качестве первого шага уберем из Z1, ребро АВ и грань α. Ясно, что для полученной области Z2 выполняется Э(Z2) очевидно, Э(Z3)=Э(Z2). Теперь уберем ребро АА1 с вершиной А. Т.к. при этом уменьшается на единицу и число ребер, и число вершин, то для полученной области Z4 выполняется Э(Z4)=Э(Z3). Продолжая действовать подобным образом, после k-го шага придем к области Zk+1, являющейся многоугольником. Но для любого многоугольника числа ребер и вершин совпадают, грань одна. Поэтому Э(Zk+1)=1. По построению, Э(Z1)= Э(Zk+1)=1, и в силу (2) Э(Z0)=2.Э(Z0)=Э(Z1)+1. (2)
Теорема доказана.
Слайд 15 Самым поучительным в приведенном доказательстве является то, что
оно верно не только для многогранников. Рассмотрим произвольную пространственную
фигуру, гомеоморфную шару. Нанесем на ее поверхность Z криволинейную сетку L разбивающую Z на конечно число областей , гомеоморфных кругу, которые мы назовем гранями. Пусть Р(Z), Г(Z) и В(Z) суть соответственно число ребер, граней и вершин сетки L и Э(Z)=В(Z)+Г(Z)-Р(Z). Отобразив Z гемеоморфно на поверхность какой-либо сферы и рассуждая аналогично предыдущему, получим Э(Z)=2. Таким образом, мы установили, что все гомеоморфные сфере поверхности Z имеют одну и ту же величину эйлеровой характеристики Э(Z)- число 2. Обратим внимание на то, что значение Э(Z) оказалось не зависящим от площади и числа граней, длин и числа ребер, углов пересечения ребер и числа верши сетки и т.д. Другими словами, эйлерова характеристика не связана с метрическими свойствами поверхностей, а отображает более глубокие свойства.Ясно, например, что объем, ограниченный поверхностью Z, или площадь Z не относятся к топологическим свойствам. В отличие от них эйлерова характеристика является топологическим свойством поверхности. Боле того, она определяет тип поверхности в том смысле, что если для какой-то поверхности эйлерова характеристика равна двум, то эта поверхность гемеоморфна сфере.
Слайд 16
Приложения теоремы Эйлера
Теорему Эйлера историки математики называют первой
теоремой топологии- раздела геометрии, который изучает свойства фигур, не
меняющихся при непрерывных деформациях, допускающих любые растяжения и сжатия, но без разрывов или дополнительных склеек.Такие свойства фигур называются топологическими. Соотношение Эйлера В-Р+Г=2 для выпуклых многогранников является как раз таким топологическим свойством. Многогранник можно как угодно деформировать, при этом ребра и грани могут искривляться, но их число, а следовательно, и соотношение Эйлера не меняются.
При доказательстве соотношения Эйлера мы уж использовали подобные деформации, когда поверхность многогранника с вырезанной одной гранью растягивали на плоскости. При этом на плоскости получался многоугольник, подразделенный на более мелкие многоугольники, для которых справедливо соотношение В-Р+Г1=1, где В- число вершин, Р- число ребер и Г1- число граней (многоугольников). Ребра и сами многоугольники могут быть искривлены, и это не влияет на соотношение Эйлера.
Слайд 17 Совокупность вершин и соединяющих их ребер на плоскости
называется графом. Примерами графов могут служить схемы метрополитена, железных
и шоссейных дорог, планы выставок, структурные формулы молекул и т.д. Графы широко используются в современной математике и программировании. Они находят все новые приложения в теории планирования и управления, теории расписаний, социологии, математической лингвистике, экономике, биологии, медицине и т.д. Исторически сложилось так, что теория графов зародилась в ходе решения головоломок двести с лишним лет назад. Одной из таких головоломок была задача о трех домиках и трех колодцах, которую мы сейчас и рассмотрим.Три соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого домика к каждому колодцу?
Решение. Предположим, что это можно сделать. Отметим домики точками D,D1,D2, а колодцы- точками К,К1,К2. Каждую точку-домик соединим с каждой точкой-колодцем. Получим 9 ребер, которые должны попарно не пересекаются.
Слайд 18 Эти ребра образуют на плоскости многоугольник, подразделенный на
более мелкие многоугольники- грани. Поэтому для числа вершин, ребер
и граней должно выполняться соотношение Эйлера В-Р+Г,=1. Добавим к рассматриваемым граням еще одну грань- Внешнюю часть плоскости по отношению к исходному многоугольнику. Тогда соотношение Эйлера примет вид В-Р+Г=2, причем В=6 и Р=9. Следовательно, Г=5. Каждая из пяти граней имеет по крайней мере четыре ребра, поскольку по условию задачи ни одна из дорожек не должна непосредственно соединять два дома или два колодца. Так как каждое ребро принадлежит ровно двум граням, то количество ребер должно быть не меньше 5х4/2=10, что противоречит условию, по которому их число равно 9. Полученное противоречие показывает, что ответ в задаче отрицателен- нельзя провести непересекающиеся дорожки от каждого домика к каждому колодцу.Слайд 19 Другой задачей-головоломкой, связанной с именем Эйлера, была задача
Эйлера о кенигсбергских мостах.
Во времена Эйлера в городе Кенигсберге
(ныне Калининград) было семь мостов через реку Прегель. Л- левый берег, П- правый берег, А и Б- остова. Можно ли, прогуливаясь по городу, пройти через каждый мост ровно по одному разу?Слайд 20 Эта задача связана с другими головоломкам, суть которых
заключалась в том, чтобы обвести контур некоторой фигуры, не
отрывая от бумаги и не обводя ни одной линии контура дважды, т.е. «нарисовать одним росчерком». Такие контуры образуют так называемые уникурсальные графы.Слайд 21 На рисунке изображен граф, соответствующий задаче о кенигсбергских
мостах. Требуется доказать, что этот граф является уникурсальным.
Для этого,
используя понятие индекса вершины , докажем, что если граф уникурсален, то он содержит не более двух вершин нечетного индекса. Действительно, если граф уникурсален и его начало не совпадает с концом, то начало и конец являются единственными вершинами нечетного индекса. Остальные вершины имеют четный индекс, так как в каждую точку мы входим и выходим из нее. Если начало совпадает с концом, то вершин с нечетным индексом нет.Приступим к решению задачи. Определим четность вершин графа на рисунке. Вершина А имеет индекс 5,Б- 3, П- 3, Л- 3.
Таким образом, мы имеем четыре вершины нечетного индекса и, следовательно, данный граф не является уникурсальным.
Отсюда получаем, что нельзя пройти во время прогулки по городу Кенигсбергу по всем семи мостам, проходя по каждому один раз.
Слайд 22
Заключение
Ознакомившись с теоремой Эйлера и ее приложениями мы
выяснили топологическую сущность эйлеровой характеристики и ее роль в
классификации поверхностей.Восхищаясь творчеством Леонарда Эйлера мы с уверенностью можем сказать, что он внес неоценимый вклад в развитие математики. Нет, пожалуй , ни одной значительной области математики, в которой не оставил бы след один из величайших математиков всех времен и народов, гений XVIII в. Леонард Эйлер.
Используемая литература