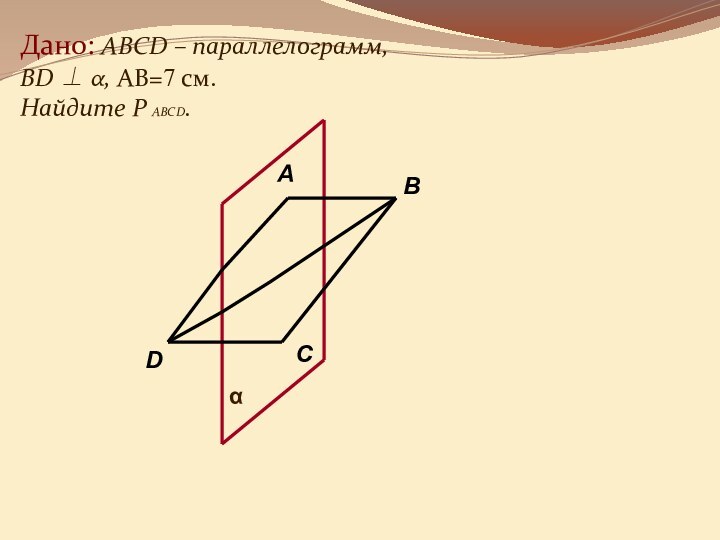
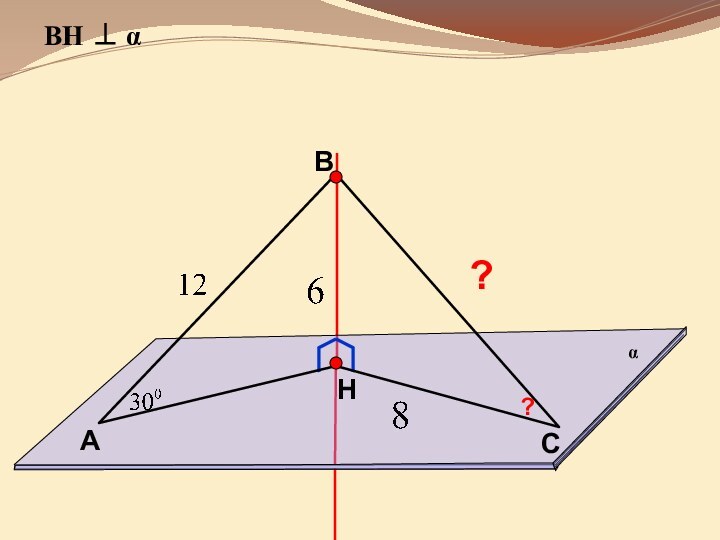
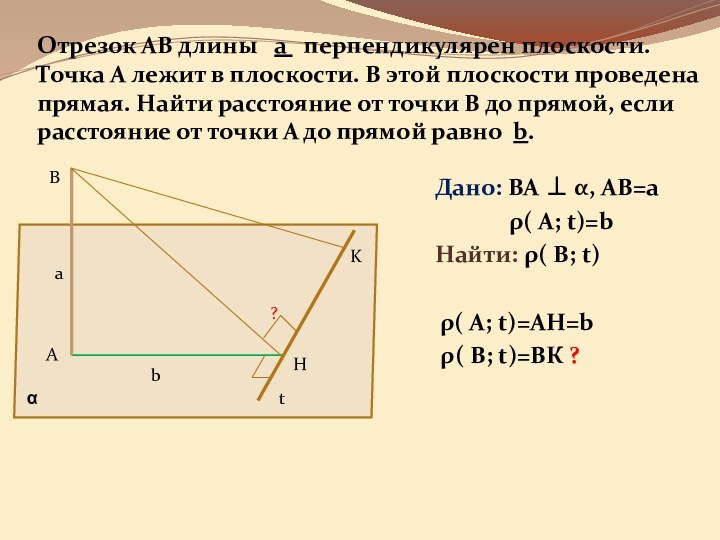
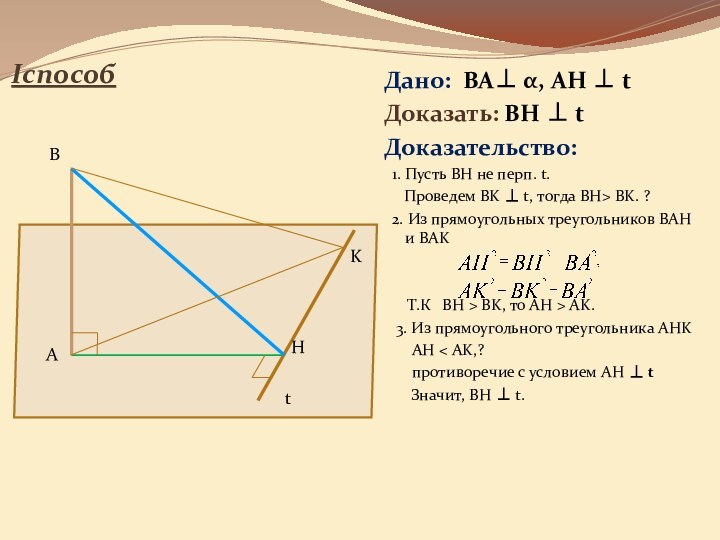
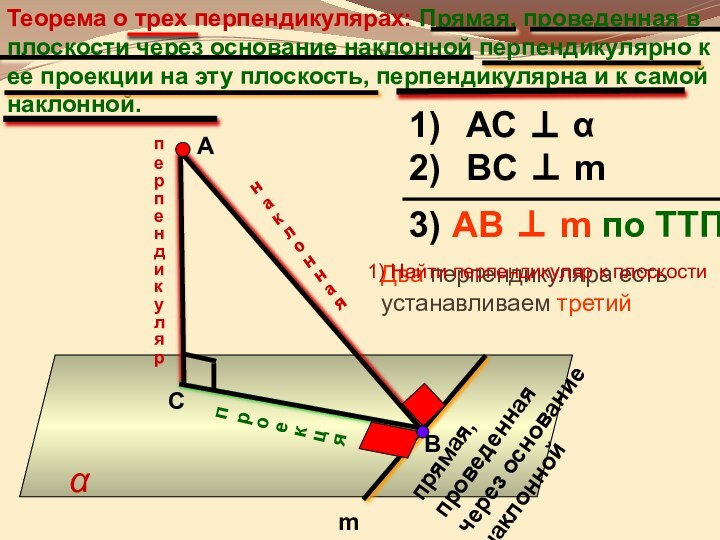
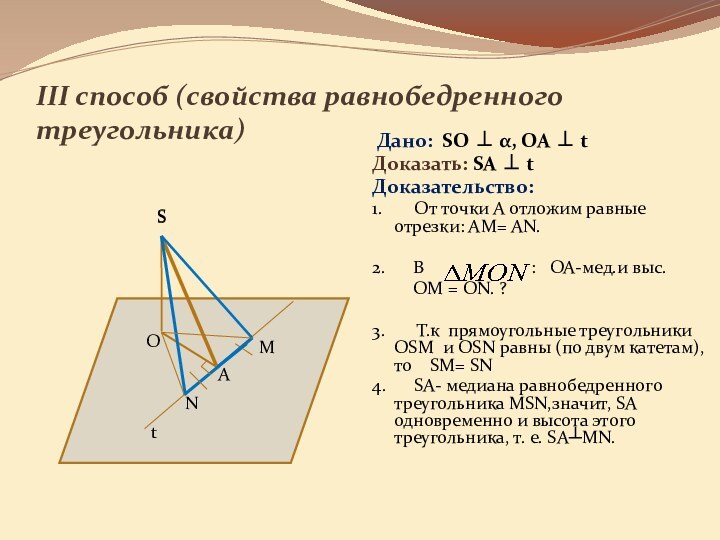
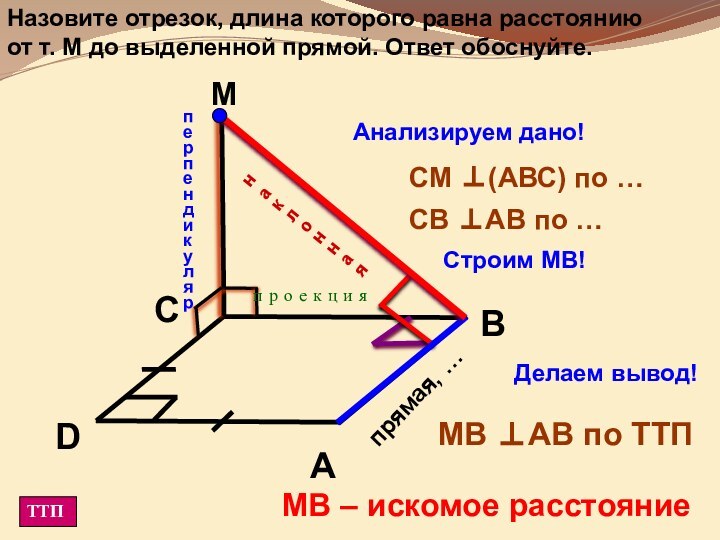
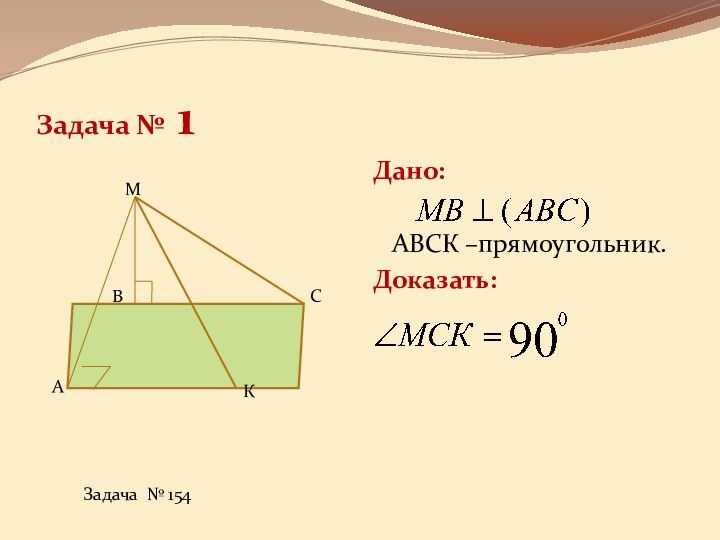
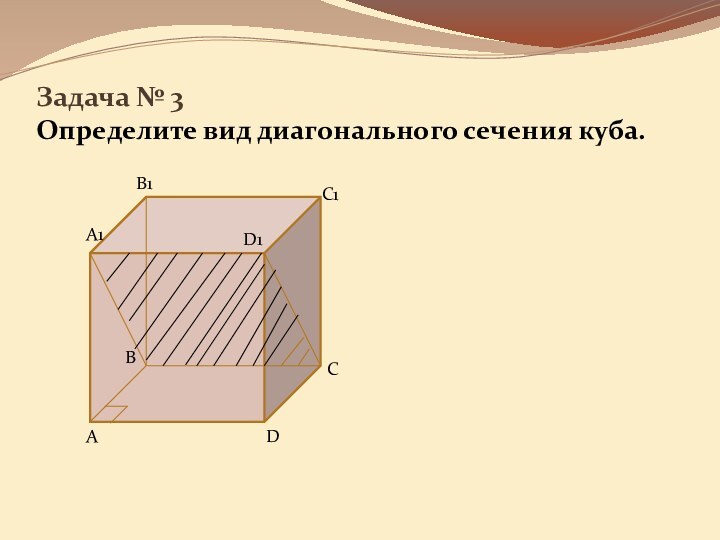
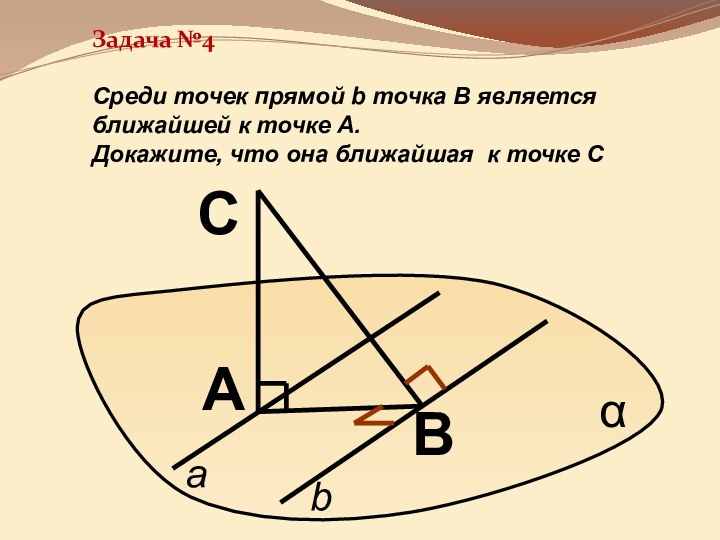
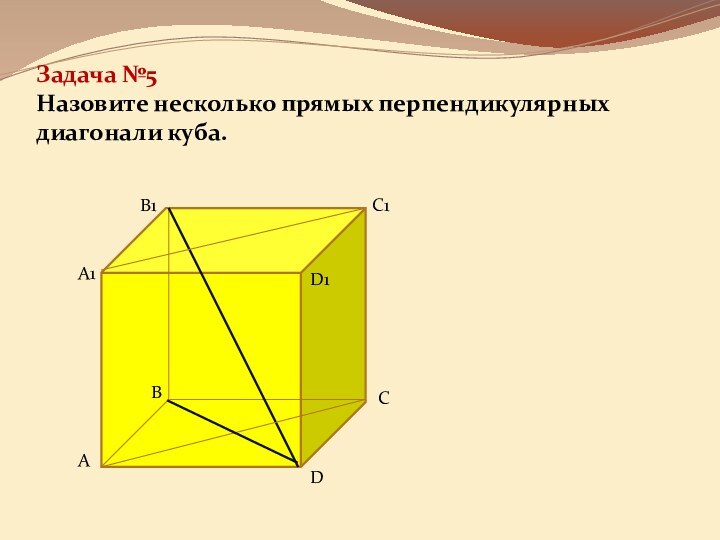
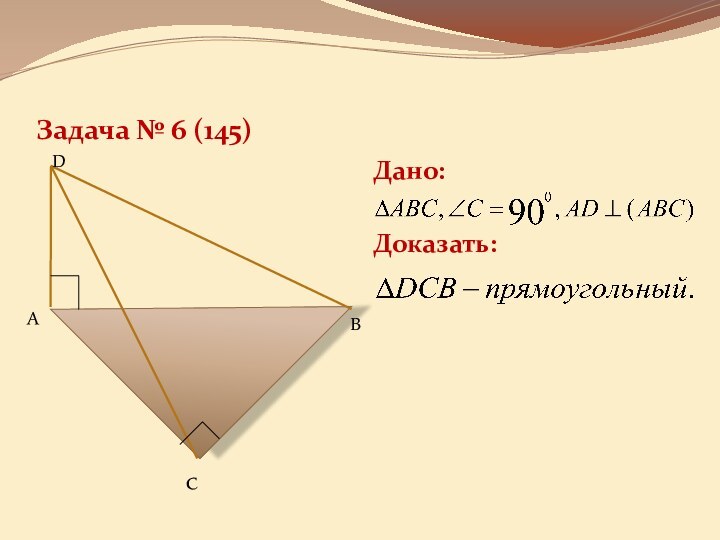
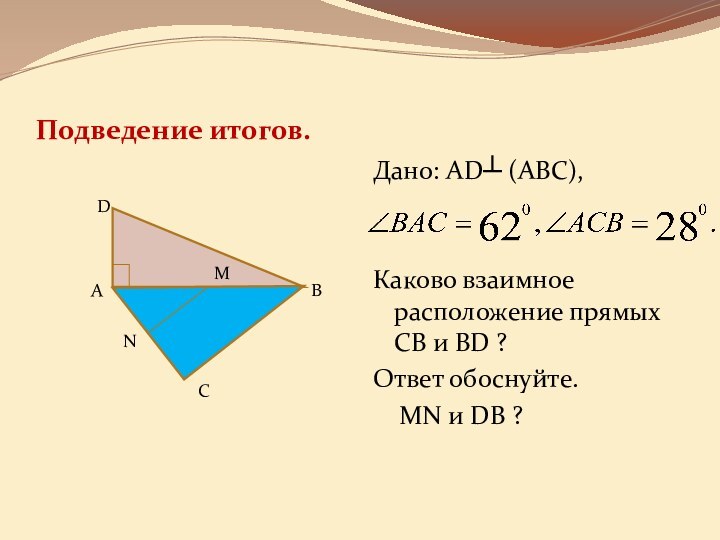
она перпендикулярна некоторой прямой, лежащей этой плоскости»
2. На
практике вертикальность столба проверяют, глядя на столб поочередно с двух направлений. Как обосновать правильность такой проверки?3. Могут ли быть перпендикулярны к плоскости две стороны треугольника одновременно?