Презентация на тему Взаимное расположение двух прямых

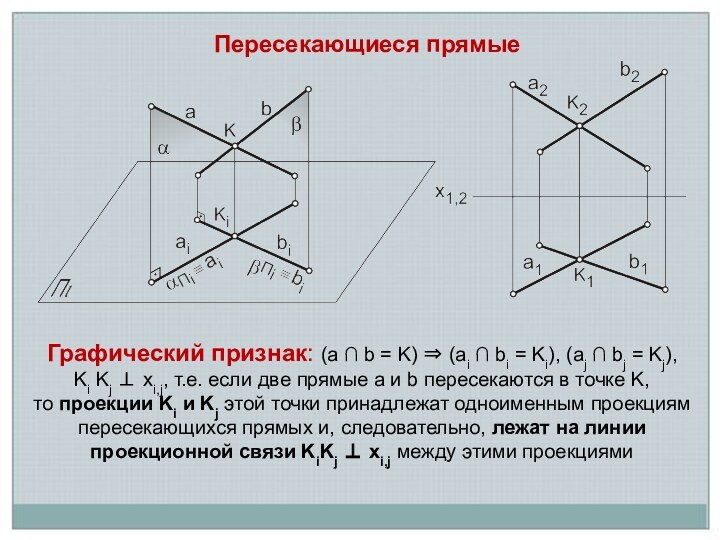
 (ai ∩ bi = Ki), (aj ∩ bj

= Kj),
Ki Kj  xi,j, т.е. если две прямые a и b пересекаются в точке K,
то проекции Ki и Kj этой точки принадлежат одноименным проекциям пересекающихся прямых и, следовательно, лежат на линии проекционной связи KiKj  xi,j между этими проекциями

проекций параллельны между собой,
то и сами прямые в

пространстве параллельны между собой

Графический признак параллельности прямых:

Параллельные прямые

на невыполнении признаков параллельности или пересечения таких прямых.
Точки пересечения

одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи, а параллельность проекций может иметь место только на одной из плоскостей проекций