- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математические оптимизационные модели и методы на основе вариационного исчисления
Содержание
- 2. Структура оптимизационной моделицелевая функция критерий оптимальностиобласть допустимых решений и системы ограничений, определяющими эту область.
- 3. Целевая функцияЦелевая функция в самом общем виде
- 4. Задача принятия решенияЗадача принятия решения называется однокритериальной,
- 5. Область допустимых решенийОбласть допустимых решений – это
- 6. б) детерминированные (А,В) и стохастические (группы кривых Сi)Стохастические ограничения являются возможными, вероятностные, случайными.
- 7. Оптимизационные задачи решаются методами математического программирования, которые
- 8. Пример. Пусть требуется выбрать геометрические размеры цилиндрического бака
- 9. Если предположить, что бак изготавливается сваркой из
- 10. Обобщенная оптимизационная модель запишется следующим образом:где y – выходная
- 11. Скачать презентацию
- 12. Похожие презентации
Структура оптимизационной моделицелевая функция критерий оптимальностиобласть допустимых решений и системы ограничений, определяющими эту область.










Слайд 2
Структура оптимизационной модели
целевая функция
критерий оптимальности
область допустимых решений
и системы ограничений, определяющими эту область.
Слайд 3
Целевая функция
Целевая функция в самом общем виде в
свою очередь также состоит из трех элементов:
управляемых переменных;
неуправляемых
переменных; формы функции (вида зависимости между ними).
Слайд 4
Задача принятия решения
Задача принятия решения называется однокритериальной, если
выбираемое решение служит достижению одной цели.
Задачи принятия решений, удовлетворяющих
нескольким целям, называются многокритериальными задачами
Слайд 5
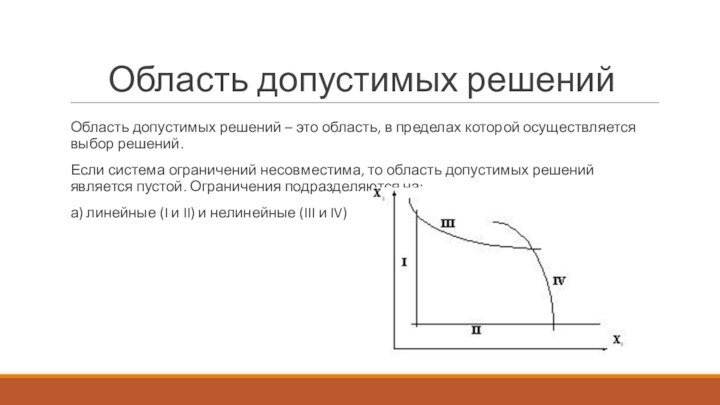
Область допустимых решений
Область допустимых решений – это область,
в пределах которой осуществляется выбор решений.
Если система ограничений несовместима,
то область допустимых решений является пустой. Ограничения подразделяются на:а) линейные (I и II) и нелинейные (III и IV)
Слайд 6
б) детерминированные (А,В) и стохастические (группы кривых Сi)
Стохастические
ограничения являются возможными, вероятностные, случайными.
Слайд 7 Оптимизационные задачи решаются методами математического программирования, которые подразделяются
на:
линейное программирование;
нелинейное программирование;
динамическое программирование;
целочисленное программирование;
выпуклое
программирование; исследование операций; геометрическое программирование и др.
Слайд 8 Пример. Пусть требуется выбрать геометрические размеры цилиндрического бака объемом V из
условия минимального расхода материала на его изготовление.
Для построения математической
модели введем в рассмотрение вектор проектных решений Х = (r, h), где r, h –радиус и высота бака .Слайд 9 Если предположить, что бак изготавливается сваркой из трех
деталей, то расход материала при произвольном векторе решений Х будет равен
площади поверхности бака: (1)
Условие того, что бак должен иметь объем заданного значения V, представим в виде:
V=pr2h. (2)
На компоненты вектора решений X необходимо наложить дополнительные условия:
R> 0, h > 0. (3)
затраты времени на изготовление бака будут пропорциональны длине свариваемых швов:
где с – затраты времени на сварку единицы длины.
(4)
Слайд 10
Обобщенная оптимизационная модель запишется следующим образом:
где y – выходная характеристика
(критерий оптимизации), которую требуется привести к экстремальному значению –
максимуму или минимуму в зависимости от ее смысла; f(X) – целевая функция, т.е. функция, описывающая зависимость критерия оптимизации от значений параметров Х; – набор из n переменных процесса, которыми можно управлять при нахождении оптимального решения, эти параметры процесса называют в теории оптимизации переменными процесса, а Х – вектором состояния процесса. функции-ограничения параметров процесса; некоторые постоянные величины, выражающие количественные значения ограничений.
В зависимости от вида функций различают модели задач линейного, нелинейного, целочисленного программирования и др.





























