Задачи с практическим
содержанием
Задачи Древнего
Китая
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










с
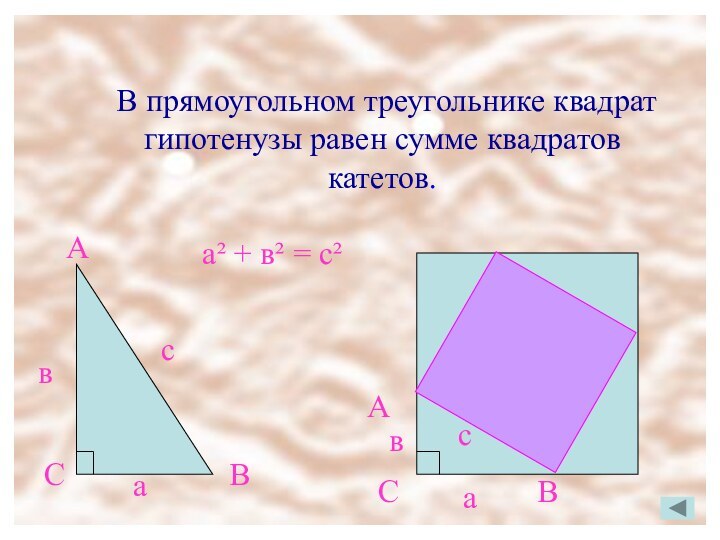
а² + в² = с²
А
В
в
с
а
С
Чертеж
Решение
13 м
5 м
h
h² = 13² - 5²
h² = 144
h = 12
Ответ: 12 метров
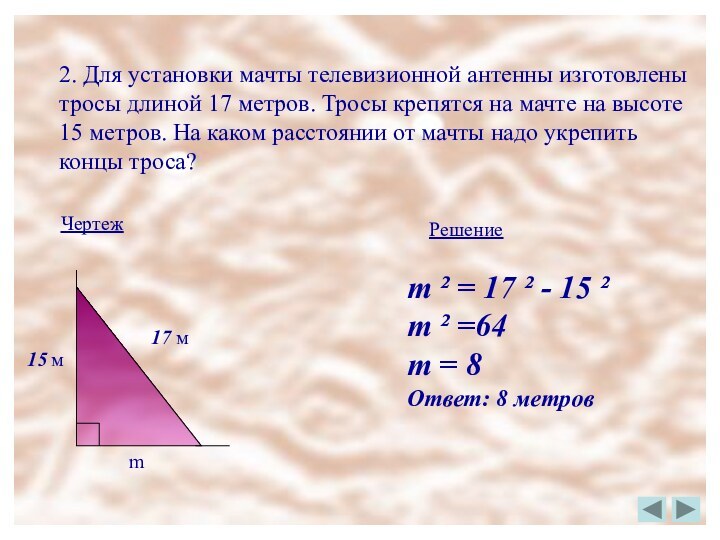
2. Для установки мачты телевизионной антенны изготовлены
тросы длиной 17 метров. Тросы крепятся на мачте на высоте
15 метров. На каком расстоянии от мачты надо укрепить
концы троса?
Чертеж
Решение
17 м
15 м
m
m ² = 17 ² - 15 ²
m ² =64
m = 8
Ответ: 8 метров
3. Вертикальная мачта поддерживается четырьмя канатами,
прикрепленными к ней на расстоянии 16 метров от земли и к земле на расстоянии 12 метров от основания мачты. Сколько метров каната потребовалось для укрепления мачты, если на узлы пошло 10 метров?
Чертеж
Решение
12 м
16 м
m
m ² = 16 ² + 12 ²
m ² = 400
m = 20
20 · 4 +10 = 90
Ответ: 90 метров
4. Длина маятника АМ=1 м, высота его подъема при отклонении в точку В на некоторый угол равна СА=10 см. Найдите расстояние от точки В до прямой МА.
Решение
x ² = 100 ² - 90 ²
x ² = 1900
x ≈ 43,6
Ответ: 43,6 см
1 подсказка: Рассмотреть
прямоугольный треугольник
МВС.
2 подсказка: Пусть ВС = х см.
По условию
МВ=100см, МС=90 см.
Пусть ВС = х см.
Задача 6
Задача 13
Имеется водоем со стороной в 1 чжан (=10 чи). В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша?
Ответ: глубина воды 12 чи, длина камыша 13 чи.
Решение
Пусть глубина воды х(смотри рисунок).
Получим прямоугольный треугольник,
у которого один катет х, второй
катет 5, а гипотенуза х+1.
Используем теорему Пифагора:
х ²+5 ²=(х+1) ².
Решим уравнение: х ²+25=х ²+2х+1
24=2х
х=12
Задача 6
Имеется бамбук высотой в 1 чжан (=10 чи). Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня. Спрашивается: какова высота после сгибания?
Решение
Пусть высота бамбука после сгибания х
(смотри рисунок).
Получим прямоугольный треугольник,
у которого один катет х,
второй катет 3, а гипотенуза 10-х.
Используем теорему Пифагора:
х ²+3 ²=(10-х) ².
Решим уравнение: х ²+9=100-20х+ х ²
20х=91
х = 4,55
Ответ: высота после сгибания 4,55 чи.
Задача 13