Слайд 2
Математические
фокусы
1
3 5
7 9 11
13 15 17 19
21 23 25 27 29
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Слайд 3
Введение
Магия не обязательно подразумевает ловкость
рук. Можно использовать математику с ее логическими механизмами. Возможности
чисел безграничны и могут привести любого в замешательство!
Математические фокусы имеют свою особую прелесть. Они очень увлекательно демонстрируют математические закономерности.
Фокусы или ещё их можно назвать эксперименты, основанные на математике, на свойствах фигур и чисел и лишь облеченные в несколько необычную форму. И понять суть того или иного эксперимента — это значит понять пусть небольшую, но точную математическую закономерность.
В математических же фокусах изящество математических построений соединяется с занимательностью.
Слайд 4
В математических экспериментах для достижения, эффективности
и занимательности как можно хитрее маскируют загадку. Именно поэтому,
вместо отвлеченных чисел часто используются различные предметы или наборы предметов, связанные с числами: домино, спички, часы, календарь, монеты и даже карты.
Математические фокусы многим нравятся больше всего по нескольким причинам:
1. Для таких фокусов не нужен большой реквизит;
2. Довольно просты в обращении;
3. Не требуют больших навыков;
4. Производят большое впечатление на зрителей.
Слайд 5
Фокусы
Карточки с числами и отверстиями
Таинственная девятка
Фокус с тремя
шашками на шахматной доске
Фокус с шестью квадратиками
Таинственные квадраты
Квадраты из
четырёх частей
Быстрое извлечение кубического корня
Угадай задуманное число
Угадай зачеркнутую цифру или феноменальная память
Слайд 6
Карточки с числами и отверстиями
Я
не знаю, когда появилось первое специальное приспособление математического характера,
предназначенное для демонстрации фокуса, или каким оно было, но кажется несомненным, что одним из самых старых фокусов, в котором оно могло потребоваться, был фокус с узнаванием задуманного им числа при помощи серии карточек с числами.
Этот фокус показывается при помощи серии карточек (обычно их бывает шесть или больше), на каждой из которых имеется ряд чисел.
Слайд 7
Зритель рассматривает все карточки и передаёт
фокуснику те из них, на которых имеется задуманное им
число.
Фокусник кладёт их друг на друга и накрывает «волшебной» карточкой.
Теперь, чтобы получить задуманное число, нужно сложить числа, видимые через отверстия.
Отверстия в «волшебной» карточке соответствуют местам, где на шести карточках расположены ключевые числа, а на каждой из шести карточек отверстия сделаны в тех же местах, что и на магической карточке, за исключением одного, где проставлено ключевое число данной карточки.
Слайд 9
Таинственная девятка
Двенадцать или более монет
размещаются на столе в форме девятки.
повернувшись спиной к зрителям. Кто-нибудь из зрителей задумывает число,
больше числа монет в «ножке» девятки, и начинает отсчитывать снизу вверх по ножке и, далее, по колечку против часовой стрелки, пока не дойдёт до задуманного числа.
Слайд 11
Затем он снова считает от единицы
до задуманного числа, начав с монеты, на которой остановился,
но на этот раз по часовой стрелке и только вокруг колечка. Под монету, на которой закончился счет, прячется маленький кусочек бумажки.
Показывающий поворачивается к столу и сразу же приподнимает монету.
Слайд 12
ОБЪЯСНЕНИЕ
Независимо от того, какое число было задумано, счет
заканчивается всегда на одной и той же монете.
А
именно, чет оканчивается на той монете, которая окажется последней, если ножку девятки монета за монетой накладывать на кольцо по часовой стрелке, начиная от монеты, следующей (по часовой стрелке) за той, к которой подходит ножка.
назад
Слайд 13
Фокус с тремя шашками на шахматной доске
Пока показывающий
стоит, отвернувшись от доски, зритель берёт три шашки и
расставляет их на доске либо по диагонали, отмеченной на рисунке
Слайд 14
тремя буквами «А», либо на противоположной диагонали, отмеченной
тремя буквами «Б», и начинает передвигать их, произнося про
себя буквы своего имени или фамилии (или и те и другие).
Слайд 15
При этом на каждую букву должен
приходиться только один ход, который можно делать любой шашкой
в любом направлении на одну клетку (шашки передвигаются только по светлым полям).
После того как вся фамилия будет произнесена, зритель может повторить всю процедуру ещё несколько раз, опять – таки выбирая шашки наугад. После этого показывающий поворачивается к зрителям и, мельком взглянув на доску, объявляет, с какого угла зритель начинал передвигать шашки: с левого верхнего или правого нижнего.
Слайд 16
ОБЪЯСНЕНИЕ
Имя и фамилия, которые нужно побуквенно произносить
про себя, должны состоять из четного числа букв. Если
имя и фамилия зрителя содержат такое число букв, можно брать как то, так и другое. Если четное число букв имеет только одно из таких слов, то предложите произносить именно это слово. Если, наконец, оба слова состоят из нечетного количества букв, то они должны произноситься друг за другом (так как сумма двух нечетных чисел четна).
Повернувшись к зрителям и взглянув на доску, обратите внимание на вертикальные четные ряды, считая из занумерованными, как на рисунке. Если в этих рядах окажется всего четное число шашек (т.е. две или ни одной), то вначале шашки стояли в правом нижнем углу, в противном случае – в левом верхнем.
назад
Слайд 17
Фокус с шестью квадратиками
Вот фокус, в
котором прикосновения к предмета сопровождаются побуквенным произношением чисел. Показывается
он на шести небольших, раскрашенных в различные цвета, квадратных пластинках, на каждой из которых изображено число.
Слайд 18
Пластинки раскладываются на столе числами вниз.
Показывающий отворачивается, а зритель в это время приподнимает одну
пластинку, смотрит на число, а затем смешивает её с остальными.
Теперь показывающий поворачивается к столу и начинает притрагиваться карандашом к пластинкам. Зритель же в это время произносит про себя побуквенно своё число так, чтобы на каждое прикосновение приходилось по одной букве. Когда все буквы замеченного числа будут исчерпаны, он произносит: «стоп».
Пластинка, на которой остановился карандаш, переворачивается, причём оказывается, что на неё как раз и есть задуманное число.
Слайд 19
ОБЪЯСНЕНИЕ
Первые шесть прикосновений делаются в произвольном
порядке. Следующие шесть – в такой последовательности: 101, 42,
45, 13, 16, 19.
Показывающему нетрудно будет выдержать этот порядок, запомнив соответствующую последовательность цветов. Конечно, этот фокус получается благодаря тому, что запись числа 101 (сто один) содержит семь букв, а запись, а запись каждого из следующих чисел – одной буквой больше
назад
Слайд 20
Таинственные квадраты
Фокусник стоит, повернувшись спиной к зрителям,
а один из них выбирает на помесячном табель -
календаре любой месяц и отмечает на нем какой-нибудь квадрат, содержащий 9 чисел.
Слайд 21
После этого зритель называет фокуснику наименьшее
из них, чтобы последний тут же, после быстрого подсчета,
объявил сумму этих девяти чисел.
Секрет фокуса прост.
Слайд 22
Фокуснику нужно прибавить к названному числу
8 и результат умножить на 9. Если m -
наименьшее число в указанном квадрате, то весь квадрат имеет вид и сумма всех чисел квадрата равна 9m + 72 = 9(m + 8).
назад
Слайд 23
Квадраты из четырёх частей
Нужно разрезать квадрат на четыре
части одинаковой формы и размера
а затем составить их по-новому
так, как показано на рисунке.
Слайд 24
При этом получается квадрат, размеры которого кажутся не
изменившимися и в то же время с отверстием посередине.
Подобным
же образом можно разрезать прямоугольник с любым соотношением длин сторон. Любопытно, что точка А, в которой пересекаются две взаимно перпендикулярные линии разреза, может при этом находиться в любом месте внутри прямоугольника.
Этот парадокс отличается сравнительной простотой, однако он много теряет благодаря тому, что даже при поверхностном изучении видно, что стороны второго прямоугольника должны быть немного больше, чем стороны первого.
Слайд 25
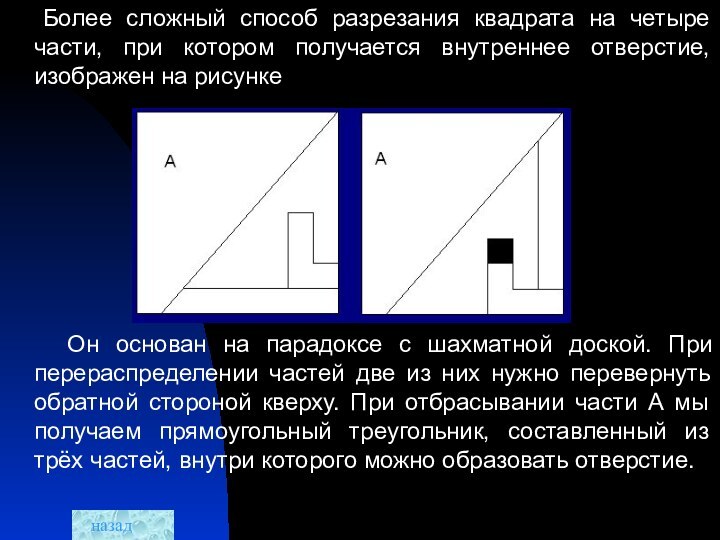
Более сложный способ разрезания квадрата на четыре части,
при котором получается внутреннее отверстие, изображен на рисунке
Он основан на парадоксе с шахматной доской. При перераспределении частей две из них нужно перевернуть обратной стороной кверху. При отбрасывании части А мы получаем прямоугольный треугольник, составленный из трёх частей, внутри которого можно образовать отверстие.
назад
Слайд 26
Быстрое извлечение кубического корня
Демонстрация фокуса с
извлечением кубического корня начинается с того, что кого-нибудь из
присутствующих просят взять любое число от 1 до 100, возвести его в куб и сообщить результат. После этого показывающий мгновенно называет кубический корень из названного числа.
Для того, чтобы показывать этот фокус, нужно сначала выучить кубы чисел от 1 до 10:
1 - 1 6 - 216
2 - 8 7 - 343
3 - 27 8 - 512
4 - 64 9 - 729
5 - 125 10 - 1000
Слайд 27
При изучении этой таблицы обнаруживается ,
что все цифры, на которые оканчиваются кубы, различны, причём
во всех случаях, за исключением 2 и 3, а также 7 и 8, последняя цифра куба совпадает с числом, возводимым в куб. В исключительных же случаях последняя цифра куба равна разности между 10 и числом, возводимым в куб.
Приведём пример
Пусть зритель, возводя некоторое число в куб, получил, например, 250047. Последняя цифра этого числа 7, из этого следует, что последней цифрой кубического корны должна быть 3.
Слайд 28
Первую цифру кубического корня находим следующим
образом. Зачеркнём последние три цифры куба (независимо от количества
его цифр) и рассмотрим цифры, стоящие впереди - в данном случае - это 250.
Число 250 располагается в таблице кубов между кубами шестёрки и семёрки. Меньшая из этих цифр – в нашем случае - 6 и будет первой цифрой кубического корня. Поэтому правильным ответом будет 63.
Ещё один пример
Пусть названо число 19683. Его последняя цифра 3 указывает, что последней цифрой кубического корня будет 7. Зачеркивая последние три цифры, получаем число 19, которое лежит между кубом двойки и кубом тройки. Меньшим из этих чисел будет 2, поэтому, искомым корнем будет 27.
назад
Слайд 29
Угадай задуманное число
Как ни странно, но очень часто
этот фокус проходит в таком примитивном варианте. Вы просите
задумать число, затем прибавить к нему два и из суммы отнять задуманное число. В результате получите число 2. Можете проделать с этим числом несколько манипуляций (например, умножить на 2, потом разделить на 4 и т.д.). Затем к полученному результату, который вы знаете, заставляете прибавить задуманное число и просите назвать сумму. Естественно, вы сразу даете ответ.
Этот фокус можно оформить как фокус на предсказание результата. В этом случае вы не просите прибавить задуманное число, а сразу называете результат.
Слайд 30
Приведем более совершенные варианты этого фокуса
Фокус
1
Предлагаете участнику написать любое трехзначное число с
условием, чтобы его первая и последняя цифры были различны. Пусть это число он перепишет в обратном порядке, а затем вычтет из большего числа меньшее. Теперь разность надо тоже переписать в обратном порядке и сложить эти два числа. Пусть теперь участник задумает какое-то число, сложит его с полученной суммой и объявит вам результат. Вы угадываете задуманное число.
Секрет фокуса
В результате манипуляций с трехзначным числом получится число 1089.
Слайд 31
541-145=396
396+693=1089
1089+54=1143
1143-1089=54
Слайд 32
Фокус 2
Вы просите зрителя
задумать какое-то число. Пусть к этому числу он прибавит
число лет, которое ему осталось до 100-летнего юбилея. К этой сумме пусть зритель добавит число людей, присутствующих на данном фокусе, включая его самого и фокусника, а затем отнимет число окон в комнате, где проходит фокус. Пусть к этой разности он добавит свой возраст и сообщит результат. Вы угадываете задуманное число.
Секрет фокуса
Сумма возраста и числа лет до столетнего юбилея всегда равна 100. Число людей, присутствующих на фокусе, и число окон в комнате вы знаете. Так что результат разности вам известен.
назад
Слайд 33
Угадай зачеркнутую цифру или
феноменальная память
Многие слышали, что
гораздо легче выучить наизусть большую поэму, чем запомнить ряд
многозначных чисел. Для меня такое запоминание является простым и лёгким.
Напишем на доске десять многозначных чисел:
1) 3751428267; 2) 92504970;
3) 875866734; 4) 11342040723;
5) 4863541275; 6) 962987157;
7) 21012043122; 8) 735183;
9) 351834959736; 10) 51624372546.
Ни одно из них, как видите, не повторяется - все они разные.
Слайд 34
Я запомнил числа, пока писал.
Если
хотите проверить, завяжите мне глаза. Из любого числа вычеркните
какую угодно цифру, а потом, не торопясь, назовите мне все цифры, которые остались. Я вам скажу по памяти, какая цифра вычеркнута.
Секрет фокуса прост!
Не нужно обладать исключительной память, чтобы показать этот фокус, построенный на простом расчёте. Все написанные числа обладают одинаковым свойством: сумма цифр каждого числа делится на 9 без остатка.
Когда вам называют все цифры любого числа без одной, вы складываете их в уме и результат вычитаете из ближайшего большего числа, которое делится без остатка на 9. Получившаяся разница и будет показывать вычеркнутую цифру.