- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора
Содержание
- 2. Задача
- 3. Задача
- 4. Задача
- 5. (ок. 580 – ок. 500 г. до н.э.)Пифагор Самосский
- 6. Открытия пифагорейцев Пифагорейцами было сделано много важных открытий
- 7. Поворотная симметрия 5-го порядка
- 8. ЗадачаДля крепления мачты нужно установить 4 троса.
- 9. c2 = a2 + b2В прямоугольном треугольнике
- 10. Пифагоровы штаны во все стороны равны
- 11. Шаржи
- 12. Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- 13. Итак, Если дан нам треугольник И притом с прямым
- 14. Рисунок – опорный сигналАС2 + ВС2 =
- 15. ЗадачаР е ш е н и е
- 16. ЗадачаР е ш е
- 17. ЗадачаР е ш е н и е
- 18. Задача. Высота, опущенная из вершины В ΔАВС,
- 19. Задача индийского математика XII века БхаскарыНа
- 20. Задача из китайской «Математики в девяти
- 21. Задача из учебника «Арифметика»
- 22. ПентаграммаМефистофель: Нет, трудновато выйти мне теперь,
- 23. Скачать презентацию
- 24. Похожие презентации


















Слайд 6
Открытия пифагорейцев
Пифагорейцами было сделано много важных открытий
в арифметике и
геометрии, в том числе:теорема о сумме внутренних углов треугольника;
построение правильных многоугольников и деление плоскости на некоторые из них;
геометрические способы решения квадратных уравнений;
деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
доказательство того, что корень из 2 не является рациональным числом;
создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.
Слайд 8
Задача
Для крепления мачты нужно установить 4 троса. Один
конец каждого троса должен крепиться на высоте 12 м,
другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?
Слайд 9
c2 = a2 + b2
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Площадь квадрата, построенного на
гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Слайд 13
Итак,
Если дан нам треугольник
И притом с прямым углом,
То
квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней
находим – И таким простым путём
К результату мы придём.
Ч.т.д.
Теорема в стихах
Слайд 14
Рисунок – опорный сигнал
АС2 + ВС2 = АВ2
АВ=AD+DB
AC2+BC2 = AB⋅(AD+DB)
AC2 = AD⋅AB
BC2 =
DB⋅AB
Слайд 15
Задача
Р е ш е н и е
Δ АВС − прямоугольный с гипотенузой АВ, по теореме Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62, АВ2 = 64 + 36, АВ2 = 100,
АВ = 10.
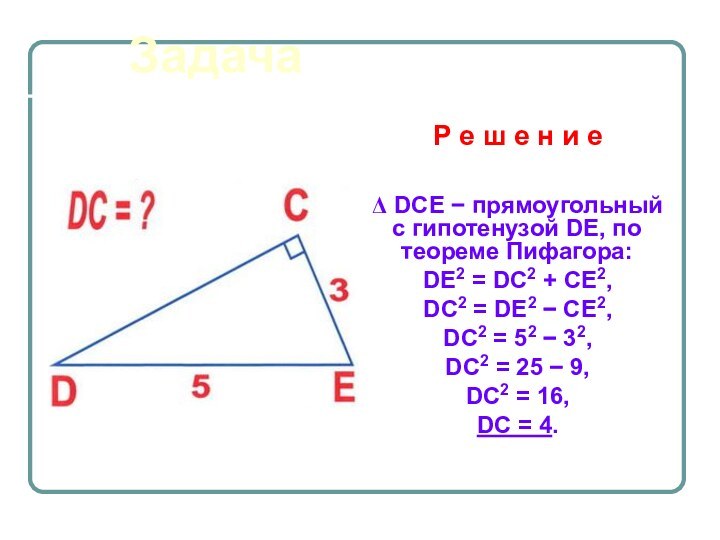
Слайд 16
Задача
Р е ш е н
и е
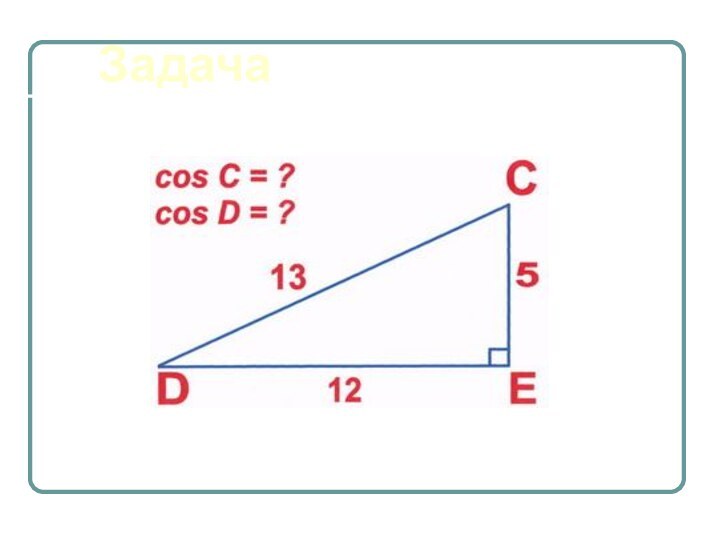
Δ DCE − прямоугольный с гипотенузой DE, по
теореме Пифагора: DE2 = DС2 + CE2,
DC2 = DE2 − CE2,
DC2 = 52 − 32,
DC2 = 25 − 9,
DC2 = 16,
DC = 4.
Слайд 17
Задача
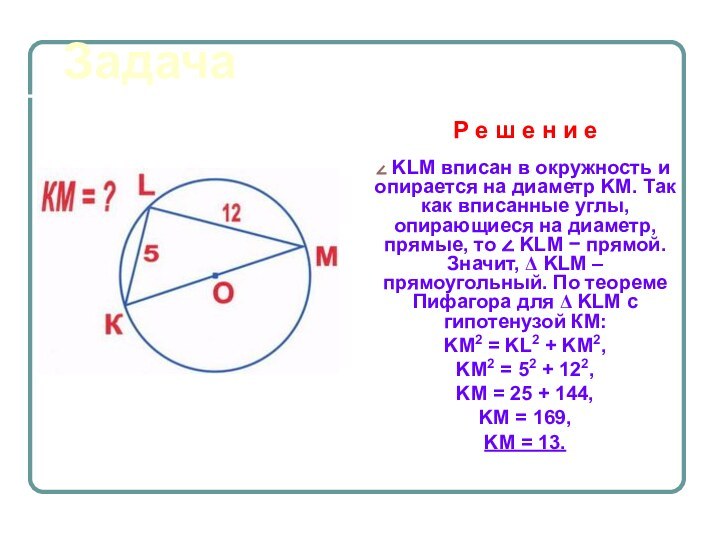
Р е ш е н и е
KLM
вписан в окружность и опирается на диаметр KM. Так
как вписанные углы, опирающиеся на диаметр, прямые, то ∠ KLM − прямой. Значит, Δ KLM – прямоугольный. По теореме Пифагора для Δ KLM с гипотенузой КМ:KM2 = KL2 + KM2,
KM2 = 52 + 122,
KM = 25 + 144,
KM = 169,
KM = 13.
Слайд 18 Задача. Высота, опущенная из вершины В ΔАВС, делит
сторону АС на отрезки, равные 16 см и 9
см. Найдите сторону ВС, если сторона АВ равна 20 см.Д а н о: Δ АВС, BD ⊥ АС, АВ = 20 см,
AD = 16 см, DC = 9 см.
Н а й т и: ВС.
Р е ш е н и е
1) По условию задачи BD ⊥ АС, значит,
Δ ABD и Δ CBD – прямоугольные.
2) По теореме Пифагора для Δ ABD:
АВ2 = AD2 + BD2, отсюда BD2 = AB2 – AD2,
BD2 = 202 – 162,
BD2 = 400 – 256,
BD2 = 144,
BD = 12 см.
3) По теореме Пифагора для Δ СBD: ВС2 = ВD2 + DС2, отсюда
BC2 = 122 + 92,
BC2 = 144 + 81,
BC2 = 225,
BC = 15см.
О т в е т: ВС = 15 см.
З а м е ч а н и е. На втором этапе решения достаточно было найти BD2 и подставить его значение в равенство ВС2 = ВD2 + DС2.
Слайд 19
Задача индийского математика
XII века Бхаскары
На берегу реки
рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь
упал. И угол прямойС теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Слайд 20
Задача из китайской
«Математики в девяти книгах»
Имеется водоем
со стороной в 1 чжан = 10 чи. В
центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?Слайд 21 Задача из учебника «Арифметика»
Леонтия Магницкого
Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.
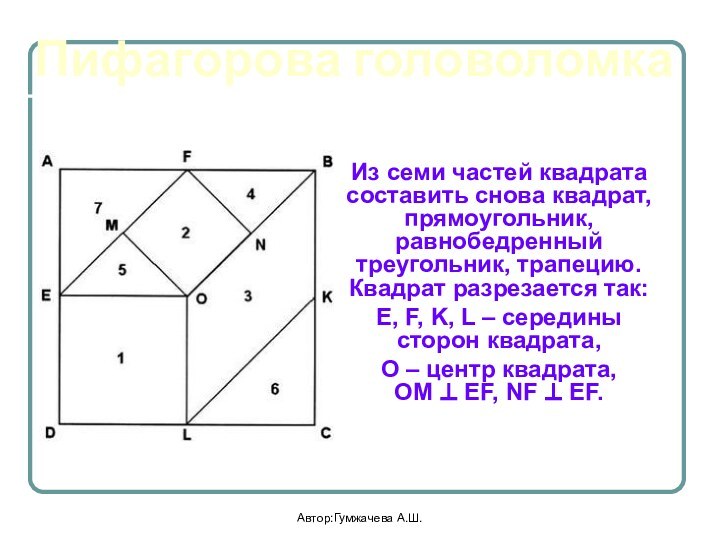
Слайд 22
Пентаграмма
Мефистофель: Нет, трудновато выйти мне теперь,
Тут кое-что мешает мне немного:
Волшебный знак у вашего порога.
Фауст: Не пентаграмма ль этому виной?
Но как же, бес, пробрался ты за мной?
Каким путем впросак попался?
Мефистофель: Изволили ее вы плохо начертить,
И промежуток в уголку остался,
Там, у дверей, - и я свободно мог вскочить.