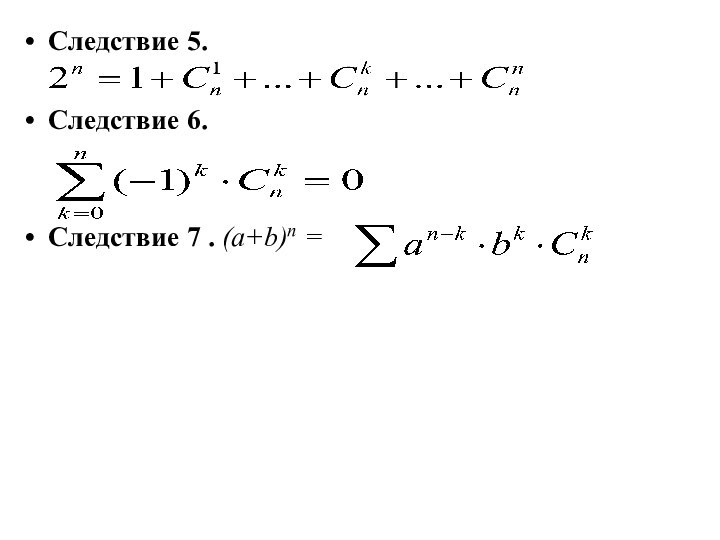Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Теория конечных множеств (комбинаторика)

Содержание

2. Если конечное множество A состоит из m
3. Доказательство: При l=2 ссылаемся на теорему 1:
4. Иногда принцип сложения можно встретить в таком
5. Теорема 3 (принцип умножения). Если множество A
6. Где множествоB'={b1, b2 ,…, bk}состоит из k
7. В комбинаторном изложении принцип умножения часто формулируют
8. Теорема 4. Если множества
9. Задача . Пусть A и B конечные
10. Задача . Из цифр A={0,1,2,3,5,6,7} составить
11. A1 = {0, 1, 2, 3},
12. Аналогично n(B2 )=n(B3 )=n(B4 )=n(B5 )=n(B6 )=n(B7
13. §2. Размещения и перестановки Определение 1. Пусть
14. Пример. Пусть A=a,b,c,d. Выпишем все 2-размещения этого
15. Теорема 2. Пусть n  N,
16. C другой стороны ,
17. Допустим, равенство выполняется для k < n,
19. Пример. В первенстве страны
20. Замечание 3. При k>n невозможно построить k-размещение,
21. Определение 5. Пусть конечное множество A состоит
22. Теорема 6. Доказательство.Применим индукцию по k.При k=1
23. Докажем утверждение при k= l +1. Из
24. Пример. Номер машины состоит из двух букв
25. Определение7. Перестановкой n-элементного множества называется упорядоченный набор длины
26. Теорема 8. Pn=n! Доказательство. Каждую
27. Задача. Сколькими способами на шахматной доске
28. §3.Сочетания. Свойства сочетаний. Бином Ньютона Определение
29. Теорема 2.
30. и отсюда получаем искомую формулу:
31. Теорема 3 (простейшие свойства сочетаний).1) 2) 3) 4) 5)
32. Теорема 4 (бином Ньютона).
33. Доказательство. Второе равенство представляет собой не что
34. Раскрыв скобки, получим суммуВ первой сумме количество
35. Число слагаемых в k-ой
36. Следствие 5. Следствие 6. Следствие 7 . (a+b)n =
37. Замечание. В силу большой
38. Определение 10. Пусть А = {a1, a2,
39. Лемма . Число всех упорядоченных нулей и
40. Скачать презентацию
41. Похожие презентации

Если конечное множество A состоит из m элементов, то мы будем писать: |A| = m или n(A) = m. Теорема 1 (принцип сложения). Пусть A B = . Тогда n(A B)

Главная
Математика
Теория конечных множеств (комбинаторика)

ТЕОРИЯ КОНЕЧНЫХ МНОЖЕСТВ (КОМБИНАТОРИКА) §1. Принципы сложения и умноженияКомбинаторика занимается

Если конечное множество A состоит из m элементов, то мы будем писать:

Доказательство: При l=2 ссылаемся на теорему 1: n(A1 A2) =

Иногда принцип сложения можно встретить в таком виде: если объект x можно

Теорема 3 (принцип умножения). Если множество A состоит из m элементов, а

Где множествоB'={b1, b2 ,…, bk}состоит из k элементов.По индуктивному предположению n(A

В комбинаторном изложении принцип умножения часто формулируют так: если объект x можно

Задача . Пусть A и B конечные мн-ва, B A.

Задача . Из цифр A={0,1,2,3,5,6,7} составить все четырехзначные числа,

Аналогично n(B2 )=n(B3 )=n(B4 )=n(B5 )=n(B6 )=n(B7 )=18По принципу произведения n(B8 )=4·3·2·1=24.

§2. Размещения и перестановки Определение 1. Пусть дано конечное множество A, n(A)=n

Пример. Пусть A=a,b,c,d. Выпишем все 2-размещения этого четырёхэлементного множества:(a;b), (b;a), (a;c), (c;a),

Допустим, равенство выполняется для k < n, то есть Докажем равенство

Теория конечных множеств (комбинаторика)

Пример. В первенстве страны участвуют 12 команд. Сколькими способами

Замечание 3. При k>n невозможно построить k-размещение, поэтому

Определение 5. Пусть конечное множество A состоит из n элементов. k -размещением

Теорема 6. Доказательство.Применим индукцию по k.При k=1 число 1-размещений равно

Докажем утверждение при k= l +1. Из каждого упорядоченного l-элементного набора можно

Пример. Номер машины состоит из двух букв русского алфавита (32 буквы) и

Определение7. Перестановкой n-элементного множества называется упорядоченный набор длины n, составленный из этих элементов,

Теорема 8. Pn=n! Доказательство. Каждую перестановку n-элементного множества можно рассматривать

Задача. Сколькими способами на шахматной доске можно расставить 8 ладей таким

§3.Сочетания. Свойства сочетаний. Бином Ньютона Определение 1. Пусть дано n-элементное множество. Любое

Теорема 3 (простейшие свойства сочетаний).1) 2) 3) 4) 5)

Доказательство. Второе равенство представляет собой не что иное, как разные

Раскрыв скобки, получим суммуВ первой сумме количество слагаемых равно количеству элементов множества

Число слагаемых в k-ой сумме равно количеству

Следствие 5. Следствие 6. Следствие 7 . (a+b)n =

Определение 10. Пусть А = {a1, a2, …, an} -

Лемма . Число всех упорядоченных нулей и единиц последовательностей из нулей и

Слайды презентации

Слайд 2 Если конечное множество A состоит из m элементов,

Если конечное множество A состоит из m элементов, то мы будем

то мы будем писать: |A| = m или n(A)

= m.
Теорема 1 (принцип сложения). Пусть A B = . Тогда n(A B) = n(A) + n(B).
Следствие 2. Пусть A1, A2….Al – система попарно непересекающихся конечных множеств.
Тогда n(A1 A2 … Al) = n(A1)+n(A2)+…+n(Al).

Слайд 3 Доказательство:
При l=2 ссылаемся на теорему 1:

Доказательство: При l=2 ссылаемся на теорему 1: n(A1 A2) = n(A1)

n(A1 A2) = n(A1) + n(A2).
Допустим, что утверждение

верно при l = k,
n(A1 A2 … Ak ) = n(A1 ) + n(A2 ) +…+ n(Ak ).
Докажем утверждение при l = k+1.
В этом случае
n(A1 A2 … Ak Ak+1) = n((A1 A2 … Ak) Ak+1) = n(A1 A2 … Ak) + n(Ak+1).
Здесь мы воспользовались базисом индукции и, применяя индуктивное предположение, получим:
n(A1 A2 … Ak) + n(Ak+1) = n(A1) +…+ n(Ak) + n(Ak+1).
Следствие доказано.

Слайд 4 Иногда принцип сложения можно встретить в таком виде:

Иногда принцип сложения можно встретить в таком виде: если объект x

если объект x можно получить m способами,

а объект y можно получить l способами, причем множества этих способов не пересекаются, то объект x или объект y можно получить m + l способами. Таким образом, необходимо помнить, что в комбинаторике союз “или” ассоциирован с операцией сложения.

Слайд 5 Теорема 3 (принцип умножения). Если множество A состоит

Теорема 3 (принцип умножения). Если множество A состоит из m элементов,

из m элементов, а множество B состоит из l

элементов, то n(A B) =ml.
Доказательство: При l=1 множествоB состоит из 1 элемента: B={b1}.
Поэтому мн-во A B={(ai, b1)|i =1, 2,…,m}состоит из m
элементов, n(A B)=m · 1=m · l.
Базис индукции проверен.
При l = k,
если n(A) = m, n(B) = k, то n(A B) = m · k.
При l = k + 1.
Пусть B = {b1, b2 ,…, bk , bk+1} или B=B‘ {bk+1},

Слайд 6 Где множествоB'={b1, b2 ,…, bk}состоит из k элементов.
По

индуктивному предположению
n(A B') = n(A) ·

n(B') = m · k.
С другой стороны B=B‘ {bk+1},
поэтому (A B) = A B' A … {bk+1},
причем A B' A {bk+1} = ,
так как B' {bk+1} = .
По теореме 1
n(A B) = n(A B' A {bk+1}) = n(A B') + n(A {bk+1})=m · k + m · 1 = m(k + 1) = m · l.

Слайд 7 В комбинаторном изложении принцип умножения часто формулируют так:

В комбинаторном изложении принцип умножения часто формулируют так: если объект x

если объект x можно сконструировать m способами, объект y

можно сконструировать l способами, то объект (x, y) или (x и y) можно сконструировать m · l способами. То есть союз “и” в комбинаторики ассоциирован с операцией умножения.

Слайд 8 Теорема 4.
Если множества A1,

Теорема 4. Если множества A1, A2, …, Ak конечны, то

A2, …, Ak конечны,
то n(A1

A2 ,…, Ak )=n(A1) · n(A2)·,…, ·n(Ak ).

Слайд 9 Задача . Пусть A и B конечные мн-ва,

B A. Сколько элементов содержит множества A\

Решение. Докажем, что в случае, когда
B A, n(A\ B) = n(A) – n(B).
В самом деле, запишем очевидное теоретико-множественное равенство
(A\ B) B = A, причем (A\ B) B = .
Применим к множествам A\ B и B принцип сложения.
n((A\ B) B)=n(A\ B) + n(B) или n(A)=n(A\ B)+n(B)
Отсюда получаем требуемое равенство n(A\ B) = n(A) – n(B).

Слайд 10 Задача . Из цифр A={0,1,2,3,5,6,7} составить

Задача . Из цифр A={0,1,2,3,5,6,7} составить все четырехзначные числа, не

все четырехзначные числа, не содержащие повторяющихся цифр и

делящиеся на 3.

Решение. Воспользуемся признаком делимости на три: число делится на три в том и только в том случае, когда сумма цифр этого числа делится на три. Поэтому надо перебрать всевозможные четверки цифр, сумма которых делится на три. Перечислим такие четверки:

Слайд 11 A1 = {0, 1, 2, 3}, A2

= {0, 1, 2, 6}, A3 = {0, 1,

3, 5},
A4 = {0, 1, 5, 6}, A5 = {0, 2, 3, 7}, A6 = {0, 3, 5, 7},
A7 = {0, 5, 6, 7}, A8 = {1, 2, 3, 6}, A9 = {1, 3, 5, 6},
A10 = {1, 2, 5, 7}, A11 = {2, 2, 6, 7}, A12 = {3, 5, 6, 7}.
Обозначим через B множество всех искомых чисел, а через Bi (i = 1, 2,…, 12) множества чисел, полученные из цифр множества Ai соответственно.
Так как при i j
Bi Bj = , то по принципу сложения

n(B) = .

По принципу произведения
n(B1)=3·3·2·1=18.

Слайд 12 Аналогично
n(B2 )=n(B3 )=n(B4 )=n(B5 )=n(B6 )=n(B7 )=18
По

Аналогично n(B2 )=n(B3 )=n(B4 )=n(B5 )=n(B6 )=n(B7 )=18По принципу произведения n(B8

принципу произведения n(B8 )=4·3·2·1=24.
Аналогично, n(B9 )=n(B10 )=n(B11 )=n(B12

)=24.
Наконец, n(B)=18·7+24·5=246

Слайд 13 §2. Размещения и перестановки
Определение 1. Пусть дано конечное

§2. Размещения и перестановки Определение 1. Пусть дано конечное множество A,

множество A, n(A)=n и 1 ≤ k ≤ n.

k-размещением множества A называется любой упорядоченный набор длины
k ( ), где все координаты - попарно различные элементы множества A. Число всех k-размещений n-элементного множества обозначается через .

Слайд 14 Пример. Пусть A=a,b,c,d.
Выпишем все 2-размещения этого четырёхэлементного

Пример. Пусть A=a,b,c,d. Выпишем все 2-размещения этого четырёхэлементного множества:(a;b), (b;a), (a;c),

множества:
(a;b), (b;a), (a;c), (c;a), (a;d), (d;a), (b;c), (c;b), (b;d),

(d;b), (c;d), (d;c).
Таким образом

Слайд 15 Теорема 2. Пусть n  N, 1

≤ k ≤ n. Тогда

Доказательство. Применим индукцию по k.
Докажем равенство при k=1.
1-размещения это наборы состоящие из одного элемента, взятого из n-элементного множества.
Очевидно, что их будет столько же, сколько
элементов, в n-элементном множестве, то есть
.

Слайд 16 C другой стороны ,

то есть

Слайд 17 Допустим, равенство выполняется для k < n, то

есть

Докажем равенство для k+1 ≤ n.
Каждый (k+1)-

элементный набор можно получить из k-элементного приписыванием справа одного допустимого элемента.
Для фиксированного k-элементного набора это будет любой элемент, не входящий в этот набор. Очевидно, что таких допустимых элементов будет n-k.
Значит, из одного k-элементного набора можно получить (n-k) (k+1)- элементных наборов, поэтому

Слайд 18

Слайд 19 Пример. В первенстве страны участвуют

Пример. В первенстве страны участвуют 12 команд. Сколькими способами они смогут

12 команд. Сколькими способами они смогут занять призовые места.

Решение. Поскольку является существенным тот факт, какая команда займет первое место, какая – второе, какая - третье, то задача сводится к вопросу: сколькими способами можно выбрать трёхэлементный упорядоченный набор из 12-элементного множества. Таких способов будет способов.

Слайд 20 Замечание 3. При k>n невозможно построить k-размещение, поэтому

при k>n.
Замечание 4. При k=0 под 0-размещением мы будем понимать пустое множество.
Так как пустое множество единственно,
то
что согласуется с формулой ,
так как при k=0 имеем

Слайд 21 Определение 5. Пусть конечное множество A состоит из

Определение 5. Пусть конечное множество A состоит из n элементов. k

n элементов. k -размещением с повторениями множества A называется

упорядоченный набор длины k, элементы которого берутся из A. Элементы в k-размещении с повторениями не обязаны быть различными.
Пример. Пусть A={1,2,3}. Выпишем все 2-размещения с повторениями множества A:
(1;1),(1;2),(1;3),(2;1),(2;2),(2;3), (3;1),(3;2),(3;3).
Число k-размещений с повторениями
n-элементного множества обозначается

Слайд 22 Теорема 6.
Доказательство.
Применим индукцию по k.
При k=1 число

Теорема 6. Доказательство.Применим индукцию по k.При k=1 число 1-размещений равно числу

1-размещений равно числу элементов множества A,

то есть
С другой стороны, n1=n. Базис индукции доказан.
Допустим, формула верна при k=l, то есть

Слайд 23 Докажем утверждение при k= l +1.
Из каждого

Докажем утверждение при k= l +1. Из каждого упорядоченного l-элементного набора

упорядоченного l-элементного набора можно получить n упорядоченных наборов длины

l+1,
приписывая любой элемент A справа, то есть
(l +1)-размещений с повторениями в n раз больше, чем l -размещений с повторениями, то есть

Теорема доказана.

Слайд 24 Пример. Номер машины состоит из двух букв русского

Пример. Номер машины состоит из двух букв русского алфавита (32 буквы)

алфавита (32 буквы) и из четырёх цифр. Сколько всего

существует номеров?

Решение. Пару букв мы можем выбрать
способами,
четвёрку цифр можно выбрать
способами.
Значит, всего машинных номеров можно составить по принципу произведения

Слайд 25 Определение7.
Перестановкой n-элементного множества называется упорядоченный набор длины n,

Определение7. Перестановкой n-элементного множества называется упорядоченный набор длины n, составленный из этих

составленный из этих элементов, причём каждый элемент входит в

набор ровно один раз.
Число перестановок n-элементного множества обозначается символом Pn .
Пример. Выпишем все перестановки 3-х элементного множества A={a;b;c}: (a;b;c),(a;c;b),(b;a;c),(b;c;a),(c;a;b),(c;b;a).
Таким образом, P3=6.

Слайд 26 Теорема 8. Pn=n!
Доказательство. Каждую перестановку

n-элементного множества можно рассматривать как n-размещение этого множества. Поэтому

Слайд 27 Задача. Сколькими способами на шахматной доске можно

расставить 8 ладей таким образом, что бы они не

били друг друга.

Решение. Первую вертикаль можно заполнить лишь одной ладьёй, чтобы не нарушалось условие задачи. Причём количество способов заполнить эту вертикаль равно восьми.
На вторую вертикаль можно поставить тоже только одну ладью, причём уже семью способами, и т.д. вплоть до восьмой вертикали, которую можно заполнить одним способами.
По принципу произведения всего способов расстановки ладей так, чтобы они не били друг друга, будет 8·7·6·…·2·1=8!

Слайд 28 §3.Сочетания. Свойства сочетаний. Бином Ньютона
Определение 1.
Пусть дано n-элементное множество. Любое

k-элементное подмножества множества A называется k-сочетанием n-элементного множества.

Число k-сочетаний n-элементного множества
обозначается .

Пример. Выпишем все 2-сочетания 4-элементного множества A={a,b,c,d}: {a;b},{a;c},{a;d},{b,c},{b,d},{c,d}.
Таким образом, .

Слайд 29 Теорема 2.

при k  n.

Доказательство. Из одного k-сочетания можно получить k! k-размещений n-элементного множества, потому что k элементов можно упорядочить k! способами.
Поскольку каждое k-размещение есть не что иное, как упорядоченное k-сочетание, то всего k-размещений будет

С другой стороны k-размещений имеется .
Получили равенство

или ,

Слайд 30 и отсюда получаем искомую формулу:

Слайд 31 Теорема 3 (простейшие свойства сочетаний).
1)

2)

3)

4)

5)

, (m1);

Слайд 32 Теорема 4 (бином Ньютона).

Слайд 33 Доказательство.
Второе равенство представляет собой не что иное,

Доказательство. Второе равенство представляет собой не что иное, как разные записи

как разные записи одной и

той же суммы. Слева стоит эта сумма в “развернутом” виде, а справа эта же сумма, записанная с помощью знака суммирования. Поэтому доказываем первое равенство.
Рассмотрим выражение:

Слайд 34 Раскрыв скобки, получим сумму

В первой сумме количество слагаемых

Раскрыв скобки, получим суммуВ первой сумме количество слагаемых равно количеству элементов

равно количеству элементов множества

то есть . Во второй сумме количество слагаемых равно количеству двухэлементных подмножеств n-элементного множества S, то есть равно .

Слайд 35 Число слагаемых в k-ой

сумме равно количеству k-элементных подмножеств

n-элементного множества S , то есть равно

Поэтому, если положить в A

то получим

Теорема доказана

Слайд 36 Следствие 5.

Следствие 6.

Следствие 7 . (a+b)n

Слайд 37 Замечание. В силу большой

важности бинома Ньютона для

самых разных разделов математики, числа называются биноминальным коэффициентами.

Следствие 9.

Слайд 38 Определение 10. Пусть А = {a1, a2, …,

an} -

n–элементное множество.
k-сочетанием с повторениями множества А называется неупорядоченный набор [a1,a2,…,ak ],
где все элементы принадлежат множеству А, причем допустимо повторение этих элементов .
Пример. Пусть А = {a, b, c}. Выпишем все 2-сочетания с повторениями множества А :
[a, a], [a, b], [a, c], [b, b], [b, c], [c,c].
Число k–сочетаний с повторениями n-элементного множества обозначается . Приведенный пример показывает, что