- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тетраэдр, виды сечений и решение задач по тетраэдру
Содержание
- 2. Цель работы:Выяснить какие виды сечений тетраэдра существуютТерминологияПоказать на примерах решения задач тетраэдра
- 3. Терминология: Тетраэдр – поверхность, составленная
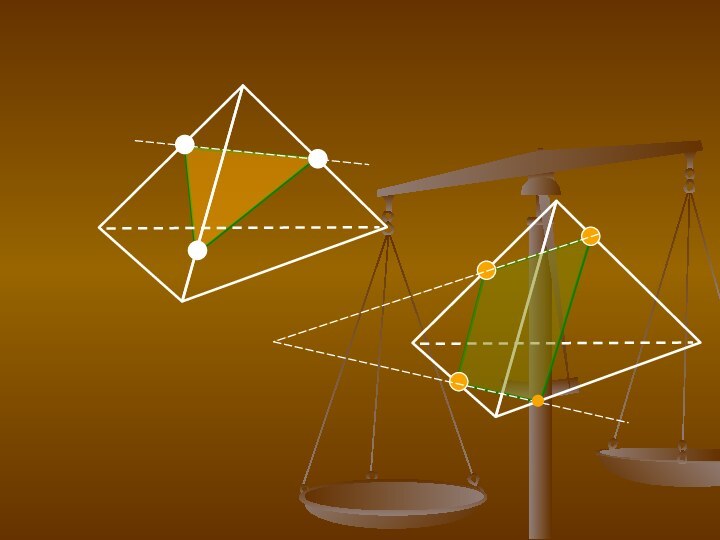
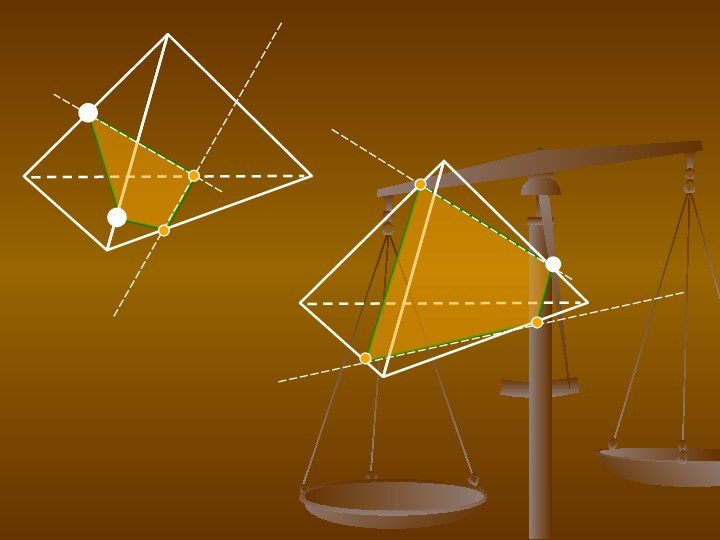
- 4. Виды сечений:
- 7. Геометрическое утверждениеЕсли две точки одной прямой лежат в плоскости, то ився прямая лежит в этой плоскости.
- 8. Задача №1Назовите все пары скрещивающихся(т.е.принадлежащих скрещивающимся прямым) ребер тетраэдра ABCD. Сколько таких пар ребер имеет тетраэдр?
- 9. Решение:В тетраэдре три пары скрещивающихся ребер:AC и DB;AB и DC;AD и CB.DBCA
- 10. Задача №2Точки М и N – середины
- 11. Решение:MN параллельны прямой, лежащей в плоскости BCD (прямой BC), поэтому она параллельна всей плоскости.ACBDMN
- 12. Задача №3 Через середины ребер AB и
- 13. Решение: Плоскость SBC и плоскость, проходящая через
- 14. Заключение:В результате работы над темой я изучил
- 15. Скачать презентацию
- 16. Похожие презентации
Цель работы:Выяснить какие виды сечений тетраэдра существуютТерминологияПоказать на примерах решения задач тетраэдра












Слайд 2
Цель работы:
Выяснить какие виды сечений тетраэдра существуют
Терминология
Показать на
примерах решения задач тетраэдра
Слайд 3
Терминология:
Тетраэдр – поверхность, составленная из
четырех треугольников
Сечение – многоугольник,
образованный при пересечении граней тетраэдра секущей плоскостью, сторонами которого являются отрезки по которым они пересекаются.
Слайд 7
Геометрическое утверждение
Если две точки одной прямой лежат в
плоскости, то и
вся прямая лежит в этой плоскости.
Слайд 8
Задача №1
Назовите все пары скрещивающихся
(т.е.принадлежащих скрещивающимся прямым) ребер
тетраэдра ABCD. Сколько таких пар ребер имеет тетраэдр?
Слайд 10
Задача №2
Точки М и N – середины ребер
AB и BC тетраэдра ABCD. Докажите, что прямая MN
параллельна плоскости BCD.
Слайд 11
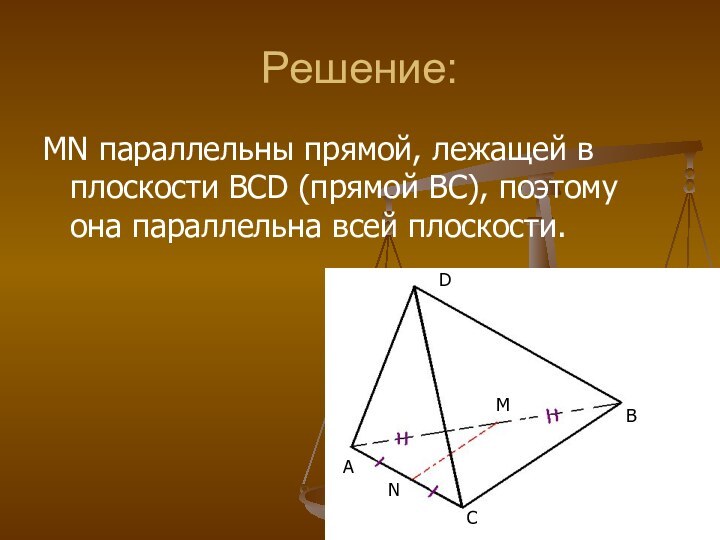
Решение:
MN параллельны прямой, лежащей в плоскости BCD (прямой
BC), поэтому она параллельна всей плоскости.
A
C
B
D
M
N
Слайд 12
Задача №3
Через середины ребер AB и BC
тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите ,
что эта плоскость пересекает грани SAB и SBC по параллельным прямым.
Слайд 13
Решение:
Плоскость SBC и плоскость, проходящая через прямую
MN параллельно ребру SB, пересекаются по прямой, проходящей через
точку N.По теореме линия пересечения параллельна SB.
В плоскости SBC через т.N проходит NQ SB.
Плоскость SAB и плоскость MNQ пересекаются по прямой, проходящей через т. М(прямая MP).
По теореме линия пересечения параллельна SB.
PM SB
NQ SB
PM NQ.
Утверждение доказано.
S
B
C
N
A
P
Q
M





























